Санкционированное получение прав доступа.

Данный способ характеризуется тем, что при передаче прав доступа не накладываются ограничения на кооперацию субъектов системы, участ­вующих в этом процессе.

Пусть х, уО - различные объекты графа доступа G₀=(S₀,O₀,E₀), R. Определим предикат "возможен доступ" (,х,у,G₀), который будет истинным тогда и только тогда, когда существуют графы G₁=(S₁,O₁,E₁),.... G_N=(S_N,O_N,E_N), такие, что:

G₀├_op1 G₁├_op2…├_opN G_N и (x,y,)E_N.

Определение 1. Говорят, что вершины графа доступов являются tg-связными или что они соединены tg-путем, если (без учета направле­ния дуг) в графе между ними существует такой путь, что каждая дуга этого пути помечена t или g. Будем говорить, что вершины непосредственно tg-связны, если tg-путъ между ними состоит из единственной дуги.

Теорема 1. Пусть G₀=(S₀,O₀,E₀) - граф доступов, содержащий толь­ко вершины-субъекты. Тогда предикат "возможен доступ" (,х,у,G₀) исти­нен тогда и только тогда, когда выполняются следующие условия 1 и 2.

Условие 1. Существуют субъекты s_l .... s_m, такие, что

(s_i,y,_i,)E₀ для i=1,...,m и  = ₁… _m.

Условие 2. Субъект х соединен в графе G₀ tg-путем с каждым субъ­ектом s_i, для i=1,...,m.

Доказательство. Проведем доказательство теоремы для m=1, так как схему доказательства для этого случая легко продолжить на случай

При m =1 условия 1 и 2 формулируются следующим образом:

Условие 1. Существует субъект s, такой, что справедливо (s,y,)E₀.

Условие 2. Субъекты х и s соединены tg-путем в графе G₀. Необходимость. Пусть истинен предикат "возможен доступ" (,x,y,G₀). По определению истинности предиката существует последователь­ность графов доступов G₁=(S₁,O₁,E₁), ...., G_N=(S_N,O_N,E_N), такая, что: G₀├_op1 G₁├_op2…├_opN G_N и (x,y,)E_N, при этом N является минимальным, т.е. (x,y,)E_N-1. Докажем необходимость условий 1 и 2 индукцией по N.

При N=0 очевидно (x,y,)E₀. Следовательно, условия 1, 2 выпол­нены.

Пусть N>0, и утверждение теоремы истинно для k<N. Тогда (x,y,)E₀ и дуга (x,y,) появляется в графе доступов G_N в результате применения к графу G_N-1 некоторого правила opN. Очевидно, это не пра­вила "Создать" или "Удалить". Если opN правило "Брать" ("Давать"), то по его определению

s' E_N-1: (x,s',t)  E_N-1 ((s',x,g) E_N-1 ), (s',y,) E_N-1 и opN = take(,x,s',y)(opN= = grant(,s',x,y)).

Возможны два случая: s'S₀ и s' S₀.

Пусть s'S₀. Тогда истинен предикат "возможен доступ" (,s',у,G₀), при этом число преобразований графов меньше N. Следовательно, по предположению индукции sS₀: (s,y,)E₀ и s' соединен с s tg-путем в графе G₀. Кроме этого, истинен предикат "возможен доступ" (t,x,s',G₀) ("возможен доступ" (g,s',x,G₀)), при этом число преобразований графов меньше N. Следовательно, по предположению индукции s"S₀:(s",s',t)E₀ и s" соединен с х tg-путем в графе G₀((s",x,g)E₀ и s" соединен с s' tg-путем в графе G₀). Таким образом, sS₀:(s,y,)E₀ и субъекты х, s соединены tg-путем в графе G₀. Выполнение условий 1 и 2 для случая s'E₀ доказано.

Пусть s' S₀. Заметим, что число преобразований графов N мини­мально, поэтому новые субъекты создаются только в тех случаях, когда без этого невозможна передача прав доступа. Следовательно, преобразо­вания графов отвечают следующим требованиям:

1) субъект-создатель берет на созданный субъект максимально не­обходимый набор прав {t,g};

2) каждый имеющийся в графе G₀ субъект не создает более одного субъекта;

3) созданный субъект не создает новых субъектов;

4) созданный субъект не использует правило "Брать для получения прав доступа на другие субъекты.

Из перечисленных требований следует, что М<N-1, s"S₀:opM =

= create ({g,f},s",s'), opN=take(,x,s',y) и истинен предикат "возможен доступ" (,s",y,G₀). Отсюда - истинен предикат "возможен доступ" (t,x,s',G_M), а так как s"-единственный субъект в графе G_M, имеющий права на субъект s', то по предположению индукции s" соединен с х tg-путем в гра­фе G₀. Из истинности предиката "возможен доступ" (,s",y,G₀) и по пред­положению индукции sS₀:(s,y,)E₀ и s", s соединены tg-путем в гра­фе G₀. Следовательно, sS₀:(s,y,)E₀ и х, s соединены tg-путем в графе G₀. Выполнение условий 1 и 2 для случая s' S₀ доказано. Индук­тивный шаг доказан.

Достаточность. Пусть выполнены условия 1 и 2. Доказательство прове­дем индукцией по длине tg-пути, соединяющего субъекты х и s.

Пусть N=0. Следовательно, x=s, (x,y,)E₀ и предикат "возможен доступ" (a,x,y,G₀) истинен.

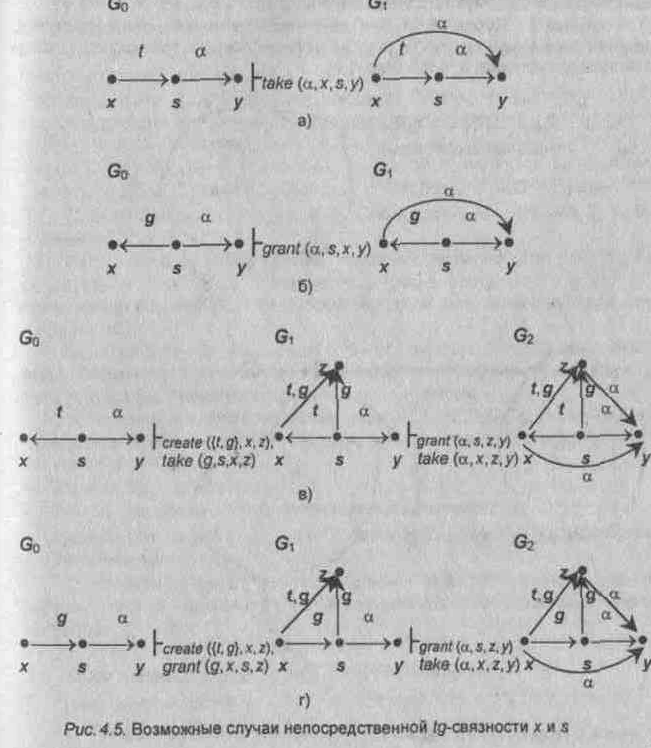
Пусть N=1, т.е. существует (s,y,)E₀ и субъекты х, s непосредст­венно tg-связны. Возможны четыре случая такого соединения х и s (рис.4.5), для каждого из которых указана последовательность преобразо­ваний графа, требуемая для передачи прав доступа.

Пусть N>1. Рассмотрим вершину z, находящуюся на tg-пути между х и s и являющуюся смежной с s в графе G₀. Тогда по доказанному для слу­чая N=1 существует последовательность преобразований графов досту­пов

G₀├_op1 G₁├_op2…├_opK G_K (z,y,)E_K и длина tg-пути между z и х равна N-1, что позволяет применить предположение индукции.

Теорема доказана.

Для определения истинности предиката "возможен доступ" в произ­вольном графе необходимо ввести ряд дополнительных понятий.

Определение 2. Островом в произвольном графе доступов G₀ назы­вается его максимальный tg-связный подграф, состоящий только из вер­шин субъектов.

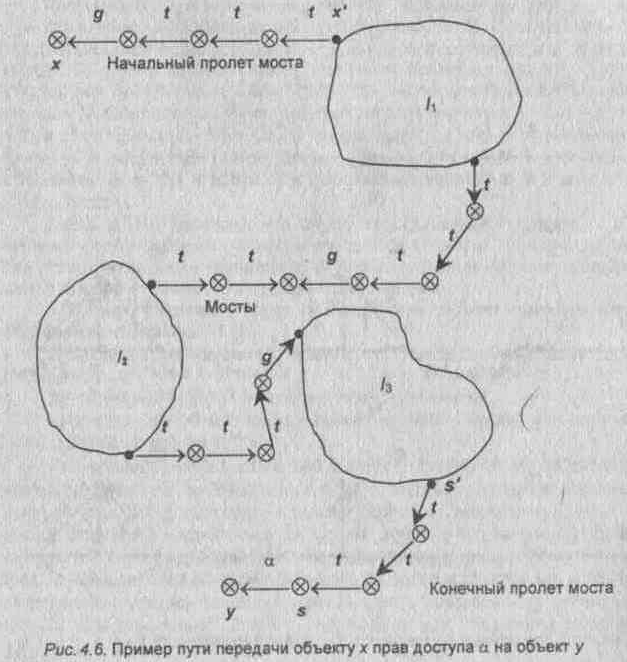
Определение 3. Мостом в графе доступов G₀ называется tg-путь, концами которого являются вершины-субъекты; при этом словарная запись tg-пути должна иметь вид ^→t*. ^←t*, ^→t*^→g^←t*, ^→t*^←g^←t*,, где символ * означа­ет многократное (в том числе нулевое) повторение.

( ^← и^→должны быть над t и g ) .

Определение 4. Начальным пролетом моста в графе доступов G₀ на­зывается tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид ^→t*^→g.

Определение 5. Конечным пролетом моста в графе доступов G₀ на­зывается tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид ^→t*.

Теорема 2. Пусть G₀=(S₀,O₀,E₀) - произвольный граф доступов. Предикат "возможен доступ"(,х,у, G₀) истинен тогда и только тогда, когда выполняются условия 3, 4 и 5 (рис. 4.6).

Условие 3. Существуют объекты s₁,...,s_m, такие, что (s_i,y,_i)E₀, i=1,...,m, и

 = ₁… _m.

Условие 4. Существуют вершины-субъекты x₁,...,x_m и s₁,...,s_m, та­кие, что:

• х=х_i или х_i, соединен с х начальным пролетом моста для i=1,...,m;

• s_i=s_i или s_i соединен с а конечным пролетом моста для i=1,.... m.

Условие 5. Для каждой пары (х_i, s_i), i=1, ...,m, существуют острова l_i,1… l_i,ui, u_i1, такие, что х_i l_i,1, s_i l_i,ui и мосты между островами l_i,j и l_i,j+1,u_ij1.

Доказательство. Проведем доказательство теоремы для m=1, так как схему доказательства для этого случая легко продолжить на случай m>1.

При m=1 условия 3, 4, 5 формулируются следующим образом:

Условие 3. sO₀: (s,y,) E_0s.

Условие 4. х', s'S₀:

• х =х' или х' соединен с х начальным пролетом моста;

• s = s' или s' соединен с s конечным пролетом моста.

Условие 5. Существуют острова l_i,...,l_u, u>1, такие, что x'l_i, s'l_u, и мосты между островами l_j и l_j+1 для j=1,...,u-1.

Необходимость. Пусть истинен предикат "возможен доступ" (,x,y,G₀). По определению истинности предиката существует последователь­ность графов доступов G₁=(S₁,O₁,E₁),...,G_N=(S_N,O_N,E_N), такая, что, G₀├_op1 G₁├_op2…├_opN G_N (x,y,)E_N при этом N является минимальным, т.е(x,y,)E_N-1. Докажем необходимость условий 3, 4. 5 индукцией по N.

При N=0 очевидно (x,y,)E₀. Следовательно, условия 3, 4, 5 вы­полнены.

Пусть N>0 и утверждение теоремы истинно для k<N. Тогда (x,y,)E₀ и дуга (x,y,)появляется в графе доступов G_N в результате применения к графу G_N-1 некоторого правила орN. Возможны два случая xS₀ и xS₀

Если xS₀, то x₁S_N-1= grant(,x₁,x,y). С учетом минимально­сти N и замечаний, сделанных при доказательстве теоремы 1, можно счи­тать, что x₁S₀. Следовательно:

1. Истинен предикат "возможен доступ" (g, x₁,x G₀) с числом преобра­зований графов, меньшим N. Тогда по предположению индукции выполне­ны условия 3, 4, 5:

• x₂O₀:(х₂,х,g) Е₀;

• x'S₀, соединенный с х₂ конечным пролетом моста;

• существуют острова l_1,…,l_t t1, такие, что x₁l_t, x'l₁, и мосты между островами l_j и l_j+1 для j=1,.... t-1;

2. Истинен предикат "возможен доступ" (,x₁,y,G₀) с числом преобра­зований графов, меньшим N. Тогда по предположению индукции выполне­ны условия 3, 4, 5:

• sO₀: (s,y, )Е₀;

• s'S₀: s=s' или s' соединен с s конечным пролетом моста;

• существуют острова l_t,...., l_u,t-u1, такие, что x₁l_t, s'l_u, и между ост­ровами l_j и l_j+1 для j=t,...., u-1.

Заметим, что путь, соединяющий вершины х',х₂,х, есть начальный пролет моста. Таким образом, для случая xS₀ условия 3, 4, 5 выполня­ются, и индуктивный шаг доказан.

Если xS₀, то п.1 условия 4 теоремы 2 очевидно выполняется. Мно­гократно применяя технику доказательства, использованную выше, можно доказать индуктивный шаг и в данном случае. Достаточность. Условия 3,4, 5 конструктивны.

По условию 3 существует объект s, который обладает правами  на объект y. По п. 2 условия 4 существует субъект s', который, либо совпада­ет с s, либо по конечному пролету моста может забрать у субъекта s права  на объект у.

По теореме 1 права доступа, полученные одним субъектом, принад­лежащим острову, могут быть переданы любому другому субъекту остро­ва. По условию 5 между островами существуют мосты, по которым воз­можна передача прав доступа. В качестве примера на рис.4.7 разобрана последовательность преобразований графа доступов при передаче прав по мосту вида ^→t^→g^←t. По п.1 условия 4 теоремы 2 существует субъект х', который или совпадает с х, или, получив права доступа, может передать их х по начальному пролету моста. Теорема доказана.