Dorofeev_A_D_P-412_Tema_vypusknoy_kvalifikatsionnoy_raboty_2

где – коэффициент использования пробега; Sгр.– пробег с грузом, км; .

S общ – общий пробег автомобиля, км.

Подставив значения в формулу (2.1) получим:

Коэффициент использования грузоподъемности автомобиля определяется по формуле:

где i – коэффициент использования грузоподъемности; Гф – фактически перевезенный груз, кг; Гн – номинальная грузоподъемность автомобиля, кг.

Транспортная задача состоит в доставке грузов от склада "ТК ЛУЧ" к

получателям. Решение этой задачи позволяет оптимизировать маршруты и способы доставки товаров, избежать лишних расходов на дальние, встречные и повторные перевозки. Это приводит к сокращению времени доставки товаров и снижению затрат компании.

Данная задача может быть решена на основе метода Свира.

Суть алгоритма Свира заключается в том, что полярная ось, подобно щетке дворника-стеклоочистителя, начинает постепенно вращаться против (или по) часовой стрелки, «стирая» при этом с координатного поля изображенных на нем клиентов — потребителей материального потока. На рисунке 2.6 изображена схема взаимного расположения склада и пунктов доставки.

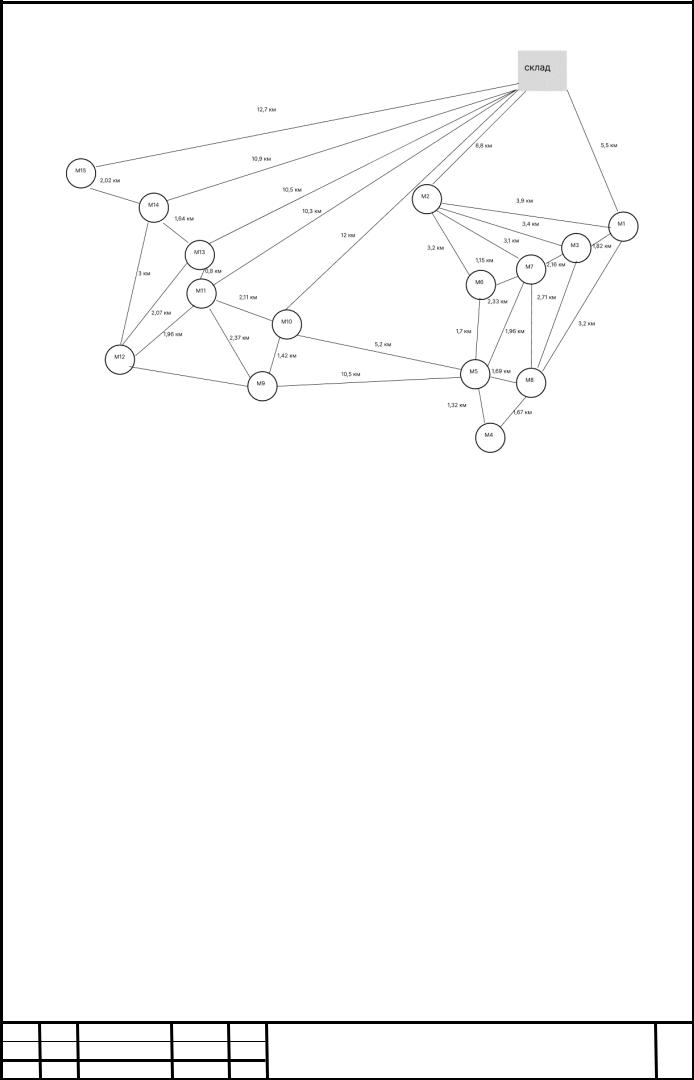
Рисунок 2.6 – Схема взаимного расположения склада и пунктов доставки

Как только сумма заказов «стертых» клиентов достигнет вместимости транспортного средства, фиксируется сектор, обслуживаемый одним кольцевым маршрутом, и намечается путь объезда потребителей.

Формирование кольцевых маршрутов завершается при полном обороте «стирающего» луча.

Алгоритм Свира позволяет подразделить всю обслуживаемую зону на несколько секторов.

Чтобы решить задачу методом Свира, необходимо определить требуемую массу груза для каждого пункта доставки, для этого составим таблицу, в которой представлена масса груза для каждого пункта.

Воображаемым лучом, исходящим со склада компании и постепенно вращающимся по или (и) против часовой стрелке, начинаем «стирать» с

транспортной сети изображенных на ней торговых точек.

В таблице 2.6 представлены пункты доставки и масса груза для каждого пункта.

Таблица 2.6 – пункты доставки и масса груза для каждого пункта.

Используя алгоритм Свира, осуществляется группировка пунктов доставки на маршруты с учетом их массы груза. В результате составляется таблица.4 предварительных маршрутов объезда пунктов назначения.

Следует отметить, что данный метод дает точные результаты лишь в том случае, когда зона обслуживания имеет разветвленную сеть дорог, а также когда расстояния между узлами транспортной сети по существующим дорогам прямо пропорционально расстоянию по прямой.

Реализацию алгоритма Свира рассмотрим на примере развозки грузов согласно условию вышепредставленной задачи.

На рисунке 2.7 представлена схема формирования маршрутов

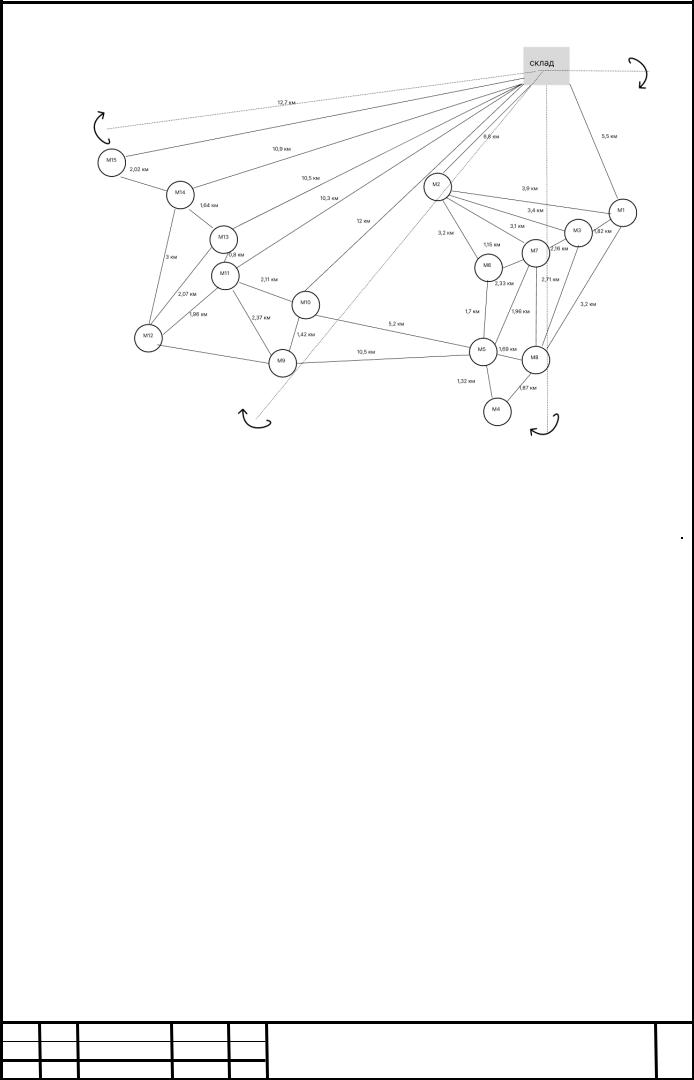
Рисунок 2.7 – Схема формирования маршрутов

Таблица 2.7 – Предварительные маршруты объезда пунктов доставки

Далее мы определяем оптимальный порядок объезда пунктов для каждого

маршрута и составляем сводную маршрутную ведомость, применяя метод ветвей и

границ, в соответствии с задачей коммивояжера.

Задача коммивояжера является одной из наиболее известных оптимизационных задач. Ее цель заключается в нахождении наиболее выгодного маршрута, который является самым коротким, быстрым, дешевым или удовлетворяет другим критериям, проходящего через все заданные точки (пункты, города) по одному разу, с возвращением в исходную точку.

Условия задачи включают в себя критерий выгодности маршрута, такой как минимальная длина, время, стоимость, а также исходные данные, представленные в виде матрицы затрат (расстояния, стоимости, время и т.д.) между рассматриваемыми пунктами.

Особенность задачи заключается в том, что она относительно проста в формулировке, и нахождение хороших решений для нее также относительно просто. Однако поиск действительно оптимального маршрута для большого набора данных является сложным и ресурсоемким процессом.

Для решения задачи коммивояжера методом ветвей и границ мы следуем определенному алгоритму:

−Построение матрицы с исходными данными, где указываются расстояния (Cij) между городами. Строкам соответствуют города отправления, столбцам - города прибытия.

−Нахождение минимумов по строкам, где в каждой строке определяется минимальное число (di) и записывается в отдельный столбец.

−Редукция строк, где из значений ячеек каждой строки вычитается соответствующий минимум (Cij = Cij - di), исключая клетки с бесконечно большим значением.

−Нахождение минимумов по столбцам, где в каждом столбце определяется минимальное число (dj) и записывается в отдельную строку.

−Редукция столбцов, где из значений ячеек каждого столбца вычитается соответствующий минимум (Cij = Cij - dj), исключая клетки с бесконечно большим значением.

−Вычисление корневой нижней границы, которая является суммой ранее найденных минимумов (H0 = ∑di + ∑dj) в стартовой (корневой) точке решения.

Затем начинается построение графа (схемы) решения с добавлением корневой вершины.

−Вычисление оценок нулевых клеток, где каждая нулевая клетка оценивается как сумма минимумов по строке и столбцу, на которых она расположена, исключая саму нулевую клетку.

−Выбор нулевой клетки с максимальной оценкой, где мы выбираем клетку с наибольшей оценкой среди нулевых клеток. Это создает две ветви решения: одна с включением отрезка пути, связанного с выбранной клеткой, и другая без включения этого отрезка.

−Редукция матрицы, где мы вычеркиваем строку и столбец, относящиеся к выбранной клетке, и заменяем значение ячейки соответствующей обратному пути на бесконечно большое число.

−Вычисление нижней границы первой ветви (включающей отрезок пути), где мы находим минимумы по строкам, выполняем редукцию строк, находим минимумы по столбцам, выполняем редукцию столбцов, а затем вычисляем локальную нижнюю границу как сумму предыдущей локальной нижней границы и минимумов (Hk = Hk-1 + ∑di + ∑dj). Затем добавляем вершину в граф.

−Вычисление нижней границы второй ветви (не включающей отрезок пути), где мы вычисляем локальную нижнюю гр аницу как сумму предыдущей локальной нижней границы и оценки выбранной ранее нулевой клетки (Hk* = Hk -1 + pij).

Затем добавляем вершину в граф.

−Выбор ветви с минимальным значением нижней границы, где мы выбираем вершину с наименьшим значением локальной нижней границы из еще не рассмотренных вершин, независимо от текущей ветви.

−Продолжение решения, если полный маршрут еще не найден. Если маршрут найден, переходим к пункту 10. В зависимости от выбранной ветви, выполняем следующие действия: а) Переходим к пункту 7 для первой ветви. б) В клетку с максимальной оценкой ставим бесконечно большое число и переходим к пункту 2 для второй ветви. в) Возвращаемся к соответствующему этапу решения и таблице данных для другой ветви.

− Построение полного маршрута и определение его длины, где мы соединяем все ранее найденные отрезки пути в полный маршрут и вычисляем его общую длину на основе исходной таблицы данных.

Это краткое описание методики решения задачи коммивояжера с использованием метода ветвей и границ.

В сети находится огромное количество калькуляторов для расчета задачи коммивояжера, поэтому воспользуемся одним из них.

На рисунках 2.8 и 2.9 представлены матрицы расстояний для расчета оптимального маршрута для первого и второго маршрута.

Рисунок 2.8 – Матрица расстояний для первого маршрута

Рисунок 2.9 – Матрица расстояний для второго маршрута

В результате расчета были получена оптимальная последовательность для первого и второго маршрута. Составим сводную маршрутную ведомость, результаты занесем в таблицу 2.8.

Таблица 2.8 – Сводная маршрутная ведомость

Чтобы оценить эффективность от использования оптимизации, необходимо рассчитать основные параметры работы подвижного состава.

Коэффициент использования пробега определяют по формуле (2.1):

Коэффициент использования грузоподъемности автомобиля определяется по формуле (2.2):

Для определения эффективности оптимизации маршрутов составим таблицу 2.9, где сравним показатели работы подвижного состава с учетом оптимизации и без нее.

Таблица 2.9 – Сравнительные показатели работы подвижного состава.

Проанализировав характеристики, можно сделать вывод о том, что, использование алгоритма Свира привело к улучшению эффективности доставки грузов, об этом говорят полученные технико-эксплуатационные показатели.

Удалось сократить длину маршрута на 26,42 км, у величить основные показатели работы транспорта, такие как коэффициент использования пробега (0,7) и коэффициент использования грузоподъемности (0,98).

2.3 Приложения для маршрутизации На рынке информационно-технологических услуг имеется ряд программных

решений, предназначенных для транспортных компаний, которые позволяют оптимизировать маршруты доставки заказов клиентам. Эти программы обеспечивают эффективное планирование маршрутов и графика движения транспортных средств, равномерное распределение нагрузки между всеми автотранспортными средствами, отслеживание местоположения автомобилей и водителей, а также формирование отчетов о фактически выполненных маршрутах.

Внедрение таких информационно-технологических решений в деятельность компаний позволяет сократить затраты на транспортировку и доставку путем эффективного планирования маршрутов, а также улучшить качество обслуживания клиентов благодаря быстрой и спланированной доставке грузов и товаров.

Давайте рассмотрим некоторые популярные программные решения и сравним их алгоритмы расчета и построения маршрутов:

− Яндекс.Маршрутизация Это сервис, который предназначен для автоматического распределения заказов

между транспортными средствами или пешими сотрудниками, а также для построения оптимальных маршрутов для каждого из них. В процессе распределения учитывается минимизация общего времени и расстояния или применение специальной целевой функции для определения общей стоимости. На рисунке 2.10 представлен интерфейс этого сервиса.

Рисунок 2.10 – Интерфейс сервиса Яндекс. Маршрутизация

Алгоритм учитывает более 50 параметров, включая виды транспорта, временные окна, параметры планирования и дополнительные ограничения. Он способен строить оптимальные маршруты для выполнения заказов, учитывая интервалы доставки, сервисное время, текущую загруженность дорог и прогноз пробок. Алгоритм также обеспечивает балансировку маршрутов, равномерно распределяя точки по количеству или длительности маршрутов. Имеется возможность точного построения маршрутов для 1000 точек всего за 15 минут.

− 1С:ТЛЭ КОРП Сервис работает на основе трех алгоритмов:

Алгоритм Очередей основан на поиске оптимального распределения заказов между транспортными средствами (ТС) с целью минимизации суммарного времени или пробега всех маршрутов. Он учитывает несколько точек погрузки/разгрузки и время, связанное с этими операциями.

Алгоритм Кларка-Райта предполагает, что все ТС в начале и конце смены будут находиться на одном и том же адресе (пункте отправления или прибытия). Он учитывает только одну отправную точку и обладает более высокой скоростью работы по сравнению с алгоритмом Очередей.

Фиксированные маршруты используются для распределения заказов по заранее заданным маршрутам с учетом порядка пунктов и назначенных ТС. Этот алгоритм