2.2. Декартова система координат

Декартовой системой координат называется совокупность точки и базиса. Если базис – ортонормированный, то декартова система называетсяпрямоугольной. Точка в этом случае называетсяначалом координати обозначается буквойО. Прямые, проходящие через начало координат в направлении базисных векторов, называютсяосями координат. В случае прямоугольной системы координат координатные оси называются, соответственно,абсциссой,ординатойиаппликатой.

Радиус-векторомточкиMв заданной системе координат называется вектор .Координатами точкиМназываются координаты ее радиус-вектора и обозначаютМ(x,y,z).

Рассмотрим две точки A(x₁,y₁,z₁) иB(x₂,y₂,z₂).Координаты векторавычисляются по формуле:

. (2.4)

Расстоянием между двумя точкамиАиВназывается длина вектораи обозначается |AB|. Следовательно,

(2.5)

Координаты точки М, делящей отрезок АВ пополамвычисляются по формуле

(2.6)

Пример 2.4.На оси ординат найти точкуМ, равноудаленную от точекА(1;–4;7) иВ(5;6;–5).

Решение. Поскольку точка М лежит на оси Oy, то М(0;y;0). По условию задачи |AM|=|BM|, отсюда

Решая это уравнение, получим y=1. Таким образом, М(0;1;0).

2.3. Векторная алгебра

Скалярным произведениемдвух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

.(2.7)

Скалярное произведение векторов обладает следующими свойствами:

10. ,	20. ,
30. ,	40. .

Отметим, что поскольку , то для скалярного квадрата используют обозначение.

Пример 2.5.Вычислить выражение, если,|,=2/3.

Решение. Раскроем скобки, учитывая свойства скалярного произведения векторов:

.

Далее из определения скалярного произведения следует:

18–24–64 = –70.

Тройка векторов называется правой, если вектора, приведенные к одному началу, располагаются также, как расставленные пальцы правой руки: большой палец – по первому вектору, указательный – по второму, средний – по третьему. Если смотреть во внутрь телесного угла, образованного этими векторами, то движение от первого ко второму, от второго к третьему будет совершаться против часовой стрелки. Обычно на практике рассматриваются только правые системы векторов.

Правая тройка	Левая тройка

Векторным произведениемвекторана векторназывается вектор, удовлетворяющий следующим условиям:

а) ,

б) вектор перпендикулярен к обоим векторами,

в) упорядоченная тройка ,,– правая.

Векторное произведение векторов обладает следующими свойствами:

10. ,	20. ,
30. ,	40. .

Пример 2.6.Вычислить выражение, если,и= 2/3.

Решение. Раскроем скобки внутри модуля, учитывая свойства векторного произведения:

.

Далее, из определения векторного произведения следует:

.

Отметим еще некоторые свойства скалярного и векторного произведений:

Два вектора иперпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю:.

Два вектора иколлинеарны тогда и только тогда, когда их векторное произведение равно нулю:.

Если два вектора иопределены своими координатами в ортонормированном базисе:,, то скалярное произведение вычисляется по формуле:

, (2.8)

а векторное произведение по формуле

(2.9)

Геометрический смысл векторного произведения:модуль векторного произведенияравен площади параллелограмма, построенного на этих векторах, как на сторонах.

Смешанным произведением векторов ,и называется числои обозначается.

Смешанное произведение векторов обладает следующими свойствами:

10.,	20. ,
30. ,	40. .

Отметим еще некоторые свойства смешанного произведения:

Три вектора ,икомпланарны тогда и только тогда, когда их смешанное произведение равно нулю:

Если три вектора ,иопределены своими координатами в ортонормированном базисе:,,, то смешанное произведение вычисляется по формуле:

(2.10)

Геометрический смысл смешанного произведения:модуль смешанного произведенияравен объёму параллелепипеда, построенного на этих векторах, как на сторонах.

Пример 2.7.Даны координаты вершин пирамидыABCD. Найти:а)объем пирамиды,б)площадь граниABC,в)косинус угла между ребрамиABиAC, еслиA(3;–2;–4),B(–5;3;4),C(1;–3;2),D(4;1;–2).

Решение. Найдем координаты векторов :

.

а) Объем пирамиды ABCD вычислим по формуле:

.

Поскольку

,

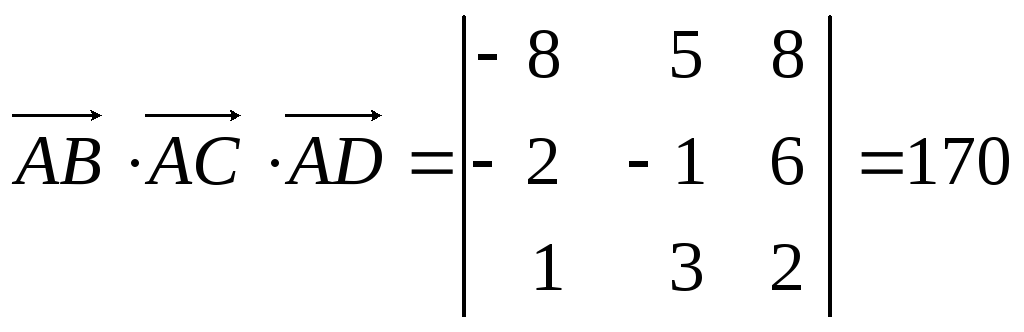то,

б) Площадь грани ABC вычислим по формуле:

.

Поскольку

,

то площадь грани ABC будет равна

в) Для того чтобы найти косинус угла между ребрами AB и AC найдем косинус угла между векторами и:

.

Тогда .