1.6. Ранг матрицы

Минором M_k k-го порядка матрицы А называется определитель k-го порядка с элементами, лежащими на пересечении любых k строк и k столбцов матрицы А.В частности, минорами 1-го порядка являются сами элементы матрицы А.В матрице А минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка равны нулю или вообще не существуют.Отметим, что в матрице может быть несколько базисных миноров, но порядок у них будет одинаковым.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначать ранг матрицыАбудем символомRgA. Матрицам с нулевым рангом соответствуют нулевые матрицы.

Пример 1.11. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:

Решение. а) Фиксируем минор 2-го порядка, неравный нулю:

Вычисляем миноры 3-го порядка, окаймляющих М₂:

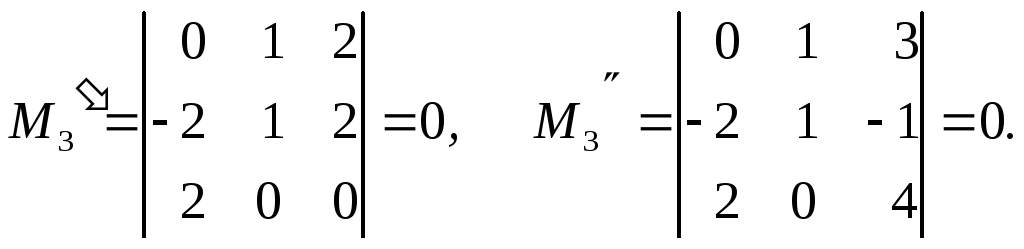
Следовательно, RgA=2, а минор М₂ – один из базисных миноров.

б) При помощи элементарных преобразований данной матрицы приведем ее к диагональному виду:

2. Векторная алгебра

2.1. Векторы и действия над ними

В геометрии под вектором(в узком смысле слова) понимается всякий направленный отрезок. Вектор с началом в точкеAи концом в точкеBпринято обозначать символом. Часто векторы обозначают одной буквой, например,. Векторы называютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых. Векторы называютсякомпланарными, если они лежат в одной плоскости или в параллельных плоскостях. Клинейнымоперациям над векторами относят операции сложения и вычитания векторов, а также умножение вектора на число.

Пример 2.1.По двум заданным векторамипостроить векторыи, еслииприведены на рисунке.

Решение. Чтобы сложить векторы, нужно совместить параллельным переносом начало и конец этих векторов. Тогда суммой этих векторов будет вектор, соединяющий начало первого и конец второго вектора (правило треугольника). Векторы можно сложить также по правилу параллелограмма, совместив начала этих векторов. Суммой векторов, в этом случае, будет диагональ параллелограмма, выходящая из начала векторов.

Разностью двух векторовиназывается сумма, т.е. чтобы вычесть из векторавектор, достаточно прибавить к векторувектор (–). Отметим, что если на векторахипостроить параллелограмм, то одна его диагональ равна сумме, а вторая – разности.

Система векторов ,, ... ,называется линейно зависимой, если найдется хотя бы одно не равное нулю числоk₁,k₂ , ... ,k_n, чтобы выполнялось равенство . Если данное равенство может выполняться только при условии, что все числаk₁,k₂ , ... ,k_nравны нулю, то такая система векторов называетсялинейно независимой. В частности, любые два коллинеарных вектора линейно зависимы; любые три компланарных вектора линейно зависимы; любые четыре 3-х мерных вектора линейно зависимы.

Линейно-независимые векторы образуют базисдля какого-либо множества векторов, если любой вектор из этого множества может быть представлен в виде некоторой линейной комбинации исходных векторов.

Пусть какая-нибудь тройка векторов образует базис в пространстве. Тогда любой вектор пространства можно разложить и притом единственным образом по этому базису:

.(2.1)

Числа a₁,a₂,a₃называютсякоординатамивекторав базисе векторов, что обозначается. Значение координат состоит в том, что операции над векторами можно сводить к действиям над числами. Тогда при сложении векторов будут складываться их соответствующие координаты, при умножении вектора на число все его координаты умножаются на это число и т.д.

Два ненулевых вектора иколлинеарны тогда и только тогда, когда выполняется равенство. Если векторы заданы в координатной форме, то условие коллинеарности будет иметь вид

(2.2)

Пример 2.2.Коллинеарны ли векторыи, еслии.

Решение. Найдем координаты векторов и:

,

.

Из условия пропорциональности

.

заключаем, что векторы иколлинеарны, причем.

Пример 2.3.Показать, что векторыобразуют базис. Найти разложение векторапо этому базису, если,,,

Решение. Векторы образуют базис, если определитель, составленный из координат этих векторов (смешанное произведение векторов) не равен нулю. Поскольку

,

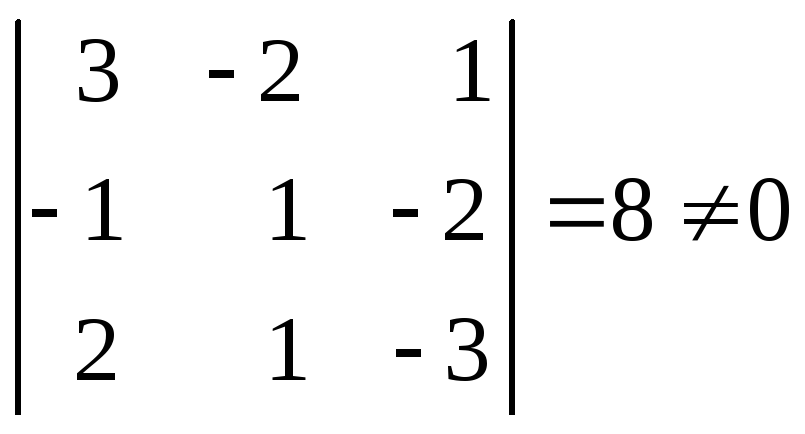то векторы образуют базис. Следовательно, векторможно разложить по этому базису:

.

Найдем числа , , . Для этого векторное уравнение распишем по координатам:

,

или

.

Два вектора равны, если равны их соответствующие координаты. Отсюда получаем систему уравнений:

Таким образом, искомое разложение имеет вид

.

Ортонормированный базис– это базис, состоящий из единичных (нормированных) и взаимно перпендикулярных (ортогональных) векторов. В этом случае базисные вектора имеют особые обозначения:. Координаты вектора в таком базисе обычно обозначаются буквамиx, y, z:. Длина вектора в ортонормированном базисе равна

(2.3)