КУРСОВАЯ_EPIFANOV_BRA2101_2 (3)

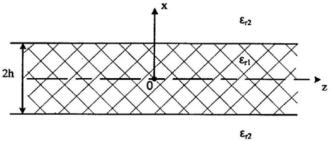
Дано:

xm(1) = Bcos(γ x)e−iβz; Exm(2) = e−α x e−iβz; Hzm(1) = Hzm(2) = 0

ξr1 = 2.6

ξr2 = 1.3

λ = 1.3 мкм

Pср(1) = 1 мВт

Задание 1.

Определить комплексные амплитуды всех проекций у векторов Em и Hm в средах 1 и 2 при x>= 0.

H m = 0 (по условию)

Комплексные амплитуды всех проекций

Eym = 0

Hxm=0

Hzm = 0

H(1)m = (γ x) e−iβz iβ

H(2m) = − e−α x e−iβz(− )

3

Задание 2.

Составить и совместно решить уравнения, связывающие неизвестные поперечные волновые числа в средах 1 и 2, т.е. γ и α

d2E(1)

xm = γ cos(γ x) γ e−iβz dx2

d2Exm(1) = cos(γ x) e−iβz (− ) dz2

−γ 2 − β2 + ω2ξa1ηa1 = 0

= −

d2Exm(2) = (−α )2 e−α x e−iβz

dx2

d2Exm(2) = A β2 e−α x e−iβz

dz2

α 2 − β2 + ω2ξa1ηa1 = 0

= −

Сложив уравнения, получаем:

α 2 + γ 2 = β2 + ω2ξa1ηa1 − β2 − ω2ξa2ηa2 α 2 + γ 2 = ω2(ξa1ηa1 − ξa2ηa2)

x = γ h;y = α h

x2 y2

h2 + h2 = ω2(ξa1ηa1 − ξa2ηa2) h2ω2(ξa1ηa1 − ξa2ηa2) = x2 + y2

= +

4

Граничные условия E при x=h требуют равенства ( ) = ( ) :

− γβ sin(γ x) e−iβz = − αβ e−αx e−iβz

γ sin(γ x) = α e−αx

α = γ tg(x)

Домножив на h получаем:

γ h tg(x) = α h

γ h ξr2 tg(x) = α h

ξr1

= γ ; y = α h

= x ξr2 tg(x)

ξr1

Построив графики по полученным двум уравнениям, мы увидим, что мы имеем две точки пересечения, что свидетельствует о распространении двух типов волны в световоде.

5

Задание 3.

Определить минимальную и максимальную толщины световода, при которых по нему будет распространяться только волна низшего типа.

Определим радиус R:

Из условия одноволнового режима (одна точка пересечения) R ≤ 3π2 , находим максимально возможную толщину h:

3

hmax = 2 π 6 = 0.855 ∙ 10−6(м) 5.508 ∙ 10

Решение трансцендентного уравнения при максимальном h

6

Из условия R ≥ π2 находим минимальную толщину h, начиная с которой существует одноволновый режим:

1

hmin = 2 π 6 = 0.285 ∙ 10−6(м) 4.776 ∙ 10

Решение трансцендентного уравнения при минимальном h

7

Найдём среднюю h световода:

Rср = 5.505 ∙ 106 ∙ 0.57 ∙ 10−6 = 3.14

Решение трансцендентного уравнения при среднем h

8

Задание 4.

Для средней толщины световода вычислить параметры волны низшего типа - γ и α

Для толщины волновода h = 0,57·10-6 м трансцендентные уравнения принимают вид:

3.142 = (α h)2 + (γ h)2

γ h 0.458 tg(γ h) = α h

Получаем:

1.339 γ = 1.339 γ = 0.57 ∙ 10−6 = 2.349 ∙ 106(м−1)

2.839 α = 2.839 α = 0.57 ∙ 10−6 = 4.981 ∙ 106(м−1)

Определим постоянные распространения волны в световоде.

β= √ω2ξr1μ1 − γ2 = √ω2ξr1ε0μ0 − γ2

=√(1,45 ∙ 1015)2 ∙ 2,6 ∙ 8,85 ∙ 10−12 ∙ 1,256 ∙ 10−6 − (2.349 ∙ 106)2

=7.433 ∙ 106 (м−1).

Фазовая скорость волны в световоде находится по формуле:

9

Задание 5.

Определить амплитуды А и В, входящие в выражения для всех проекций векторов

1

∏ = 2 Re{Ėxm Ḣym}

срz

Поставляем значения и получаем:

Отсюда можно выразить B:

Коэффициент A можно найти из граничных условий:

(γ x)e−iβz = e−α x e−iβz

(γ x) = e−α x

= (γ x) = 87.482 мА

10