Закон Био-Савара-Лапласа

Закон Био-Савара-Лапласа позволяет рассчитать вектор индукции АВ магнитного поля, создаваемого элементом проводника Δс токомi в точке О, положение которой относительно Δ определяется радиус-вектором (рис. 2).

Математически этот закон выражается в виде:

(6)

В соответствии с векторным произведением векторов А/ и /*, результирующий вектор АВ перпендикулярен плоскости с векторами А/ и г, а его направление определяется правилом правого винта, т.е. если смотреть вдоль направления вектора АВ, то кратчайший переход между направлениями векторов А/ и г осуществляется по часовой стрелке. Для модуля магнитной индукции АВ получаем выражение:

(7)

Магнитное поле любого тока в среде может быть вычислено как векторная сумма полей, создаваемых отдельными элементарными участками тока:

В = (8)

или, переходя к бесконечно малым приращениям:

B= (9)

что для модуля магнитной индукции дает выражение

(10)

Расчет вектора магнитной индукции в центре кругового тока. Воспользовавшись законом Био-Савара-Лапласа, найдем значение вектора магнитной индукции В в центре кругового тока I. Радиус контура с током полагаем равным (рис. 3).

I-dl fa

Каждый элемент тока I-dl создает в центре О витка элементарный вектор магнитной индукции dB, направленный по нормали к плоскости контура. Поэтому при интегрировании можно воспользоваться выражением (10) для скалярных величин. Учитывая, что угол а между элементом тока I-dl и радиус-вектором г₀ для всех элементов тока равен /2, a sina = 1, получаем:

_{_} (11)

Если круговой ток содержит N витков, то величина В в центре станет в N раз больше, т.е.:

(12)

Магнитное поле Земли и его характеристики

Земля представляет собой постоянный магнит, и вокруг Земли существует постоянное магнитное поле, которое содержит небольшую переменную составляющую (около 1%), обусловленную колебательными

электрическими процессами в земной коре. В настоящее время природа этого магнитного поля окончательно не выяснена, и не существует теории, которая могла бы полностью объяснить происхождение и особенности земного магнетизма, хотя практически это явление используется человечеством с античных времен для возможности ориентировки на местности с помощью магнитной стрелки (компаса), указывающей направление юг-север.

На рисунке 4а схематически изображено магнитное поле Земли. Здесь показаны магнитные силовые линии этого поля и отмечены точки земной поверхности, в которых направление силовых линий, соответствующее направлению вектора магнитной индукции земного поля, перпендикулярно поверхности Земли. Эти точки являются магнитными полюсами Земли, а прямая, их соединяющая - магнитной осью Земли.

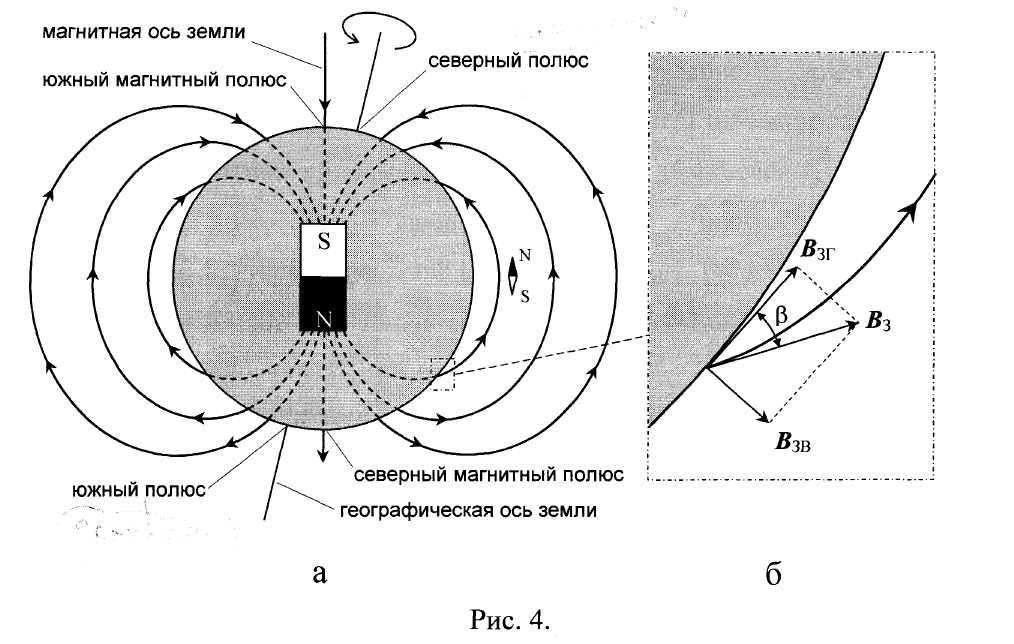
Магнитная ось не совпадает с осью вращения Земли, т.е. ее географической осью. Точки пересечения последней с земной поверхностью определяются как географические полюса Земли (или просто - северный и южный полюс),

относительно которых и формируется координатная сетка Земли, задающая координаты всех точек земной поверхности.

Необходимо отметить, что поскольку, по определению, северный конец магнитной стрелки компаса указывает на север, то вблизи северного полюса должен находиться южный магнитный полюс Земли и, соответственно, вблизи южного — северный магнитный. Координаты магнитных полюсов в результате постепенного изменения направления магнитной оси не являются постоянными. Так, за последние 60 лет, начиная с 1950 года, южный магнитный полюс сместился из точки с координатами 71° северной широты и 96° западной долготы (в районе северной Канады) более, чем на 10° к северу и почти на 20° к западу (82° С.Ш., 115° З.Д.).

Плоскость, проходящая через какую-либо точку Земли и ее магнитные полюса, называется плоскостью магнитного меридиана, а плоскость, проходящая через какую-либо точку Земли и ее географические полюса, называется плоскостью географического меридиана. Для произвольной точки поверхности Земли эти две плоскости не совпадают, т.к. не совпадают магнитные и географические полюса Земли. Угол а между плоскостью магнитного меридиана и плоскостью географического меридиана, проведенными в данной точке Земли, называется углом магнитного склонения (рис.5).

Магнитное склонение считается положительным (или восточным), если северный конец магнитной стрелки отклонен к востоку от географического меридиана, и отрицательным (или западным), если он отклонен к западу. Для точной ориентировки по магнитным приборам необходимо учитывать значение магнитного склонения, рассчитанное для данного места и для данного времени (вследствие постепенного смещения магнитных полюсов). Так, в конце 2010 года магнитное склонение для Санкт-Петербурга, Москвы и Екатеринбурга составляло соответственно +9.5°, +10° и +16.5° (восточное склонение), а для Иркутска, Владивостока и Якутска: -3°, -10° и -16° (западное склонение).

Магнитное поле различно в различных точках Земли. Величина вектора магнитной индукции B₃ вблизи поверхности Земли изменяется как по модулю (от -0.3-10^-4 Тл вблизи экватора до -0.7-10^-4 Тл на полюсах), так и по направлению относительно плоскости поверхности Земли. Угол между горизонтальной плоскостью, проведенной в данной точке земной поверхности и направлением вектора B₃ в этой точке, называется магнитным наклонением (рис. 4б). На экваторе этот угол почти равен нулю, на полюсах он стремится к 90°, в любом другом месте Земли может принимать различные значения. Вектор В₃ может быть разложен на две составляющие -горизонтальную В_3Г и вертикальную В_3В (^см- Р^ис- 4б). Соотношения между модулями этих величин:. 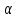Величины, и В_3Г однозначно определяют величину и направление вектора магнитной индукции В₃ в данной точке земного поля и составляют элементы Земного магнетизма.