Глава 3. Принятие решений на основе применения моделей и методов линейного программирования

1. Постановка и формализация задачи линейного программирования

Существует множество форм деятельности предприятий, которые связаны с распределением ресурсов. Эти ресурсы включают труд, сырье, оборудование и денежные средства. Процесс распределения ресурсов называется программированием.

Так как, как правило, размеры ресурсов ограничены, возникают определенные проблемы. Если предприятие выпускает продукцию нескольких видов с использованием одного и того же оборудования и трудовых ресурсов, то его руководство должно решить, какое количество продукции каждого вида производить за определенный период времени. Принятое решение будет направлено на удовлетворение определенной цели предприятия. Например, руководство может задаться целью, наладить производство таким образом, чтобы максимизировать общий выпуск продукции за месяц или максимизировать время использования оборудования за неделю.

В общем случае, цель состоит в определении наиболее эффективного метода распределения ресурсов по соответствующим видам работ, который оптимизирует некоторый результат функционирования системы.

Очень часто полезным инструментом в процессе распределения ресурсов являются методы математического программирования.

Математическим программированием называется использование математических моделей и методов для решения проблем программирования развития сложных систем. Существует ряд различных методов, основанных на идеях математического программирования, рассмотрим только один из них, который нашел наиболее широкое применение, линейное программирование (ЛП).

ЛП – является подходящим методом для моделирования процесса распределения ресурсов, если цель и ограничения на ресурсы можно выразить количественно в форме линейных взаимосвязей между переменными через параметры системы.

Этот метод включает в себя ряд шагов:

1. Необходимо осуществить математическое описание (формализацию) задачи ЛП. Это означает, что нужно идентифицировать (определить) управляемые переменные, цель задачи и систему ограничений. Затем с помощью этих переменных цель и ограничения описываются в форме линейных соотношений.

2. После завершения формулировки задачи ЛП рассматриваются все допустимые сочетания значений переменных. Из них выбирается то, которое оптимизируют целевую функцию задачи. Если исследуемая задача содержит только две переменные, то ее можно решить графически. Однако, в случае исследования задачи со многими переменными (n>2) необходимо прибегнуть к одному из алгебраических методов (например, симплекс-методу) решения задачи ЛП. Эти методы реализованы в специальных пакетах прикладных программ (например, оптимизационные системы Lindo, Lingo и др.).

3. Когда оптимальное решение получено, производится его оценка. Она включает в себя анализ задачи на чувствительность.

Замечание. Решение задачи ЛП, как и любой иной математический инструмент, применяемый в теории принятия решений, является лишь одним из факторов, влияющих на конечное решение, принимаемое руководством предприятия.

Рассмотрение моделей ЛП начнем с проблемы формулировки задачи.

Формулировка задачи ЛП. Основная процедура является общей для формулировки любой задачи ЛП:

Шаг 1. Определение переменных задачи, значение которых нужно получить в пределах существующих ограничений.

Шаг 2. Определение цели и ограничений на ресурсы.

Шаг 3. Описание цели через переменные задачи.

Шаг 4. Описание системы ограничений через переменные задачи.

Постановка задачи математического программирования в общем виде. Во многих приложениях производственная (деловая) ситуация формализуется в виде задач математического программирования (МП).

В общем виде задача МП представляет собой задачу поиска экстремума (максимума или минимума) функции нескольких переменных f (x₁, x₂, .., x_n) при наличии условий (ограничений), накладываемых на допустимые значения этих переменных:

g (x₁, x₂, .., x_n) { <, >,, }b_i,

где 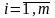; b_i – некоторые действительные числа.

Функцию f (x₁, x₂, .., x_n) называют целевой функцией (критерием оптимальности или критерием эффективности). Запись {, <,, >,} означает, что может иметь место неравенство вида , <, уравнение или неравенство вида , >.

Каждый набор значений переменных x₁, x₂, .., x_n (n-мерный вектор), удовлетворяющий всем ограничениям задачи, называется допустимым решением или планом.

Множество всех допустимых решений задачи образует область допустимых решений. Каждому решению (плану) соответствует определенное значение целевой функции.

Допустимое решение, которому соответствует максимальное (в задаче максимизации) значение функции f, называется оптимальным решением и обозначается x*=(x₁*, x₂*, .., x_n*).

Решить задачу МП – это значит найти ее оптимальное решение x₁*, x₂*, .., x_n* и соответствующее ему значение целевой функции f* = f(x*) = f(x₁*, x₂*, .., x_n*).

Задача МП, в которой целевая функция f и функции ограничений g_i , являются линейными функциями непрерывных переменных x₁, x₂, .., x_n , называется задачей ЛП.

К числу базовых задач ЛП относятся общая распределительная задача, транспортная задача и др.