
Учебные пособия / Эдельштейн лекции по ТММ учебник
.pdf
где pb, рт, рс — отрезки из плана скоростей (в этом положении механизма угол φз = 0 и, следовательно, cos φз = 1).
4)Находим приведенную силу посредством рычага Жуковского (второе решение). Строим повернутый план скоростей (рис. 73, г) и переносим в него силы Рп, Р2 и Р3 параллельно самим себе в одноименные точки. Записываем равенство моментов этих сил относительно полюса плана р (масштаб плана скоростей сокращается)
но так как
то
5)Приведенную массу находим из равенства кинетических энергий (54):
где T1, T2, T3 – кинетические энергии звеньев 1, 2 и 3,
т п — приведенная масса,
Выразим угловые скорости через соответствующие линейные:
и подставим их значения в выражение для приведенной массы, заменив в нем скорости отрезками из плана скоростей, тогда получим окончательно
В решенном примере отношение скоростей от положения к положению механизма будет меняться и, следовательно, приведенная масса будет переменной величиной, зависящей от положения ведущего звена
Пример 2. Дана рядовая зубчатая передача (рис. 74, а). К колесу 4 приложен момент М4, (моменты, направленные против часовой стрелки, будем считать положительными). Числа зубцов z на колесах, а также их моменты инерции I относительно осей вращения О известны. Найти приведенные к колесу 1 (рис. 74, б ) момент Мп и момент инерции Iп
Решение. 1) Находим М п из равенства мощностей.

Знак минус указывает, что приведенный момент Mп направлен по часовой стрелка
2) Находим приведенный момент инерции Iп из равенства кинетических энергий:
В решенном примере приведенный момент инерции будет постоянной величиной вследствие постоянства передаточных отношений.

ЛЕКЦИЯ ДЕВЯТАЯ
§ 9.Механические характеристики машин. Основные уравнения движения ведущего звена механизма. Решение задачи об истинном движении ведущего звена при условии, что приведенный движущий момент МД, приведенный момент сопротивления МС и приведенный момент инерции IП зависят от координаты ведущего звена φ1
1°. Из предыдущей лекции знаем, что изучать движение механизма проще, если рассматривать только движение одного ведущего звена.
Мы будем выбирать ведущим звеном такое, которое входит во вращательную кинематическую пару со стойкой. Тогда, после приведения усилий (сил и моментов) и масс, будем иметь дело с вращающимся звеном АВ (рис. 75), к которому приложены приведенный движущий момент МД и приведенный момент сопротивления МС , а приведенная масса этого звена оценивается его приведенным моментом инерции IП.
Положение ведущего звена определяется его угловой координатой φ1. Наша задача найти истинный закон движения этого звена, т. е. выявить одну из следующих четырех зависимостей:
Знание любой из них позволит легко найти остальные, так как
Исходными данными для нахождения зависимостей (57) будут МД, МС и IП. Эти параметры могут быть постоянными и переменными. Их изменяемость зависит: 1) от механизма, который под лежит исследованию (какое будет передаточное отношение его) и 2) от механических характеристик тех машин, которые образовали тот агрегат, в который входит исследуемый механизм (этот пункт касается только приведенных моментов движущих сил и сил сопротивления.
2°.Механической характеристикой машины называется зависимость усилия (силы или момента), приложенного к рабочему органу ее, от кинематических параметров (перемещения или скорости) этого органа.
В некоторых случаях эта зависимость отсутствует и это усилие либо постоянно, либо является функцией других параметров, например, времени.
Рассмотрим характеристики некоторых машин. Начнем с двигателей.

Гиревой двигатель (рис. 76), для него момент на его валу будет величиной постоянной, поэтому характеристика отвечает равенству
М = QR.Пружинный двигатель (рис. 77, а), его характеристика дана на рис. 77,6, очевидно, что Мд= Мд (φ). Электродвигатели: постоянного тока, его характеристика представлена на рис. 78, а, асинхронный переменного тока, его характеристика показана на рис. 78,6. Для этих двигателей момент на их валах Мд=Мд (ω).
Карбюраторный двигатель внутреннего сгорания имеет характеристику, указанную на рис. 79, а, т. е. МД=МД (ω). Здесь имеется
в виду изменение среднего за один динамический цикл машины движущего момента на ее валу. Если рассматривать изменение движущего усилия внутри динамического цикла, то механическая характеристика четырехтактного карбюраторного двигателя будет представлена его индикаторной диаграммой (рис. 79,6) и РД = PД(S). Рабочий процесс этой диаграммой описывается так: первый такт — сжатие, кривая ab;второй такт — рабочий ход, кривая bcdφ ; третий такт — выхлоп, кривая dφe ; четвертый такт — всасывание, кривая еа. В верхней части (рис. 79, б) показаны крайние положения поршня П' и П" и промежуточное — на рабочем ходу П"'. В этом положении давление
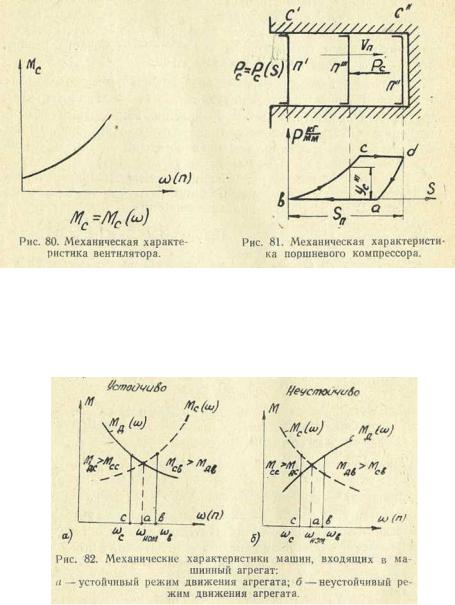
на поршень определится ординатой упиндикаторной диаграммы. Рабочие машины: вентилятор, его характеристика дана на рис. 80 и момент на его валу Мс = Мс(ω) ; строгальный станок, при малом изменении скорости суппорта сила резания остается постоянной, следовательно, его характеристика Ррез = const; поршневой компрессор, характеристика за один динамический цикл дана индикаторной диаграммой (рис. 81). Следовательно,
РС = РС(S). Рабочий процесс этой диаграммой описывается так: всасывание, кривая ab ; сжатие, кривая Ьс; нагнетание, кривая cdφ;расширение остатка, кривая dφa.В верхней части (рис. 81) показаны положения поршня: крайние П' и П" и промежуточное при сжатии П'". Давление на поршень в этом положении определяется ординатой ус" индикаторной диаграммы.
При подборе двигателя к рабочей машине всегда надо иметь в виду их механические характеристики и, в частности, для устойчивой работы агрегата эти характеристики должны располагаться так, как это указано на рис. 82, а. Установившееся движение его,
очевидно, отвечает скорости, когда механические характеристики пересекаются. Если угловая скорость превысит значение номинальной, то в этом случае момент сопротивления станет больше движущего и агрегат автоматически выйдет на установившийся режим. При уменьшении угловой скорости момент сопротивления станет меньше движущего и опять агрегат сам выйдет на стационарный режим. При расположении характеристик по рис. 82, б
устойчивого движения не будет, так как при ωв>ωωном машина пойдет в разнос, а при ωс<ωωном она будет останавливаться.
3°. Выведем основные уравнения движения ведущего звена механизма. Па рис. 83 показано ведущее звено АВ. Положение его определяется углом φ1, к нему приложены приведенные момент движущих сил Мд и момент сил сопротивления Мс, приведенная масса его оценивается ее приведенным моментом инерции Iп (в общем случае Iп = Iп(φ1)).

Сообщим звену АВ элементарное перемещение dφ1, тогда по закону сохранения энергии
сумма элементарных работ внешних сил равна дифференциалу кинетической энергии).
Продифференцировав выражение (58) по углу φ1получим
или, так как
то
Это выражение называется «уравнением движения в форме моментов» или уравнением движения механизма в форме «уравнением Лагранжа 2-го рода», из которого вытекает следствие: равномерное движение звена возможно и при неравенстве моментов МДи Мс. Для равномерного движения твердого тела с постоянной массой равенство МД и Мс обязательно. В этом заключается отличие динамики механизма от динамики твердого тела с постоянной массой.
Для получения уравнения движения ведущего звена в форме«уравнения энергий» сообщим ему конечное перемещение от углаь φ1j до угла φ1k. Проинтегрировав выражение (58) в указанных пределах угла повора ведущего звена, найдем
т. е. работа, полученная машиной в избытке (Аизб), идет на приращение ∆Tjkкинетической энергии
ее.Всегда надо указывать, на каком интервале (угле поворота) вычислялась избыточная работа Задачи об истинном законе движения ведущего звена решаются либо уравнением (58 а), либо
(58 б). Прежде чем начинать решение задач динамики механизмов, надо привести все силы (моменты) и массы к ведущему звену и установить, функциями каких параметров будут приведенные МД, Мс и Iп.
4°. Решение задачи об истинном законе движения ведущего звена при приведенных движущем моменте, моменте сопротивления и моменте инерции, зависящих от положения (координаты) ведущего звена, т. е. МД = МД(φ1), Мс = Mc(φ1)и Iп = Iп (φ1). Такая задача, например, возникает при исследовании движения механизма прибора, ведущее звено которого приводится в движение пружиной, а сопротивлением будет трение в кинематических парах этого механизма.
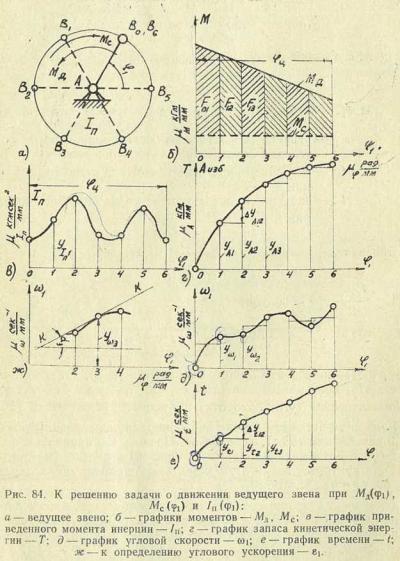
На рис. 84, а показано ведущее звено АВ. Это звено начинает двигаться из положенияBo- Кинематический цикл механизма равен одному обороту звена АВ. Найдем закон движения звена
АВ за
один оборот его. На рис. 84, б и в построены графики моментов движущих сил, сил сопротивления и приведенного момента инерции.
Решение. 1) Делим угол φц на т равных частей (в нашем случае на 6) и подсчитываем избыточную работу на каждом интервале перемещения ведущего звена:

По формуле (60) вычисляем значения угловой скорости и строим ее график (рис. 84, д).
3) Время, за которое ведущее звено А В переместится из положения jв положение к,
По формуле (62) подсчитываем время к концу каждого перемещения ведущего звена и строим график t = t (φ1)(рис. 84, е), который дает искомую зависимость (57)
4) Для нахождения углового ускорения ведущего звена можно поступать различно: а) исключать параметр φ1из выражений ω(φ1), t(φ1) и построить график ω1= ω1 (t). Дифференцированием (графическим) этой функции определим искомое угловое ускорение: б) угловое ускорение найдем по формуле
 (63)
(63)
для выбранного положения, например третьего (рис. 84,ж), проведем к кривой ω1 = ω1(φ1) касательную kk, определим угол αз наклона ее с осью абсцисс и искомое угловое ускорение

§ 10. Решение задач об истинном законе движения ведущего звена для случаев когда:а)моменты сил движущих
и сопротивления зависят от скорости, а приведенный момент инерции постоянен и б) приведенный момент движущих сил зависит от скорости, приведенный момент сил сопротивления зависит от координаты, а приведенный момент инерции тоже является функцией этой же координаты. (Эта тема изучается факультативно)
1°. Случай (а ), который соответствует агрегату, состоящему из электродвигателя, вентилятора и редуктора с постоянным передаточным отношением.
Моменты Mд и МС заданы своими графиками (рис. 85, а), приведенный момент инерции Iп= const. Для этого случая целесообразно найти закон движения ведущего звена на стадии его разгона, т. е. на интервале, когда угловая скорость изменяется от нуля до своего номинального значения (номинальная скорость — скорость установившегосядвижения)
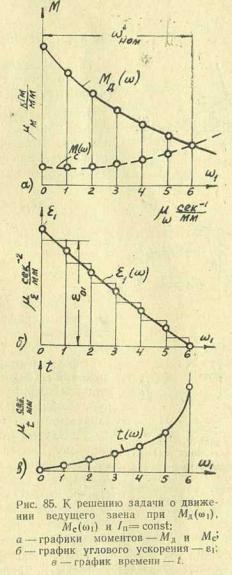
Решение. 1) Разделим исследуемый интервал изменения угловой скорости на т равных частей (в нашем случае на шесть), и, используя уравнение (58 а), вычислим значения углового ускорения:
