Учебные пособия / Эдельштейн лекции по ТММ учебник

равную угловой скорости кулачка, но противоположной ей по знаку. Теперь кулачок 1 остановится, а стойка 3 и штанга 2 будут двигаться с угловой скоростью ω1. Относительная линейная скорость штанги относительно стойки сохранит свое значение. Пусть кулачок повернется на угол φ1. Надо определить перемещение штанги, соответствующее этому углу поворота. Начальное положение штанги определяется линией А у и конец штанги В2 лежит на профиле кулачка 1. При повороте кулачка на угол φ1 линия Ау в относительном движении повернется на угол — φ1 и займет положение Ау', а конец штанги займет положение В2 S. Проведя окружность радиуса АВ2 S, найдем положение конца штанги при повороте кулачка на угол φ 1 Это положение обозначено В2 ". Перемещение штанги соответственно будет равно В2 В2 ".

Задачу о скоростях для этих механизмов можно решать двояко: либо, предварительно построив заменяющий механизм, строить планы для соответствующих групп Ассура, либо решить уравнение типа (14).

На рис. 44, а показан кулачковый механизм. Уравнение типа (14) для него будет

где υ —скорость точки B1 принадлежащей кулачку;

B 1

υ —скорость точки В2 , принадлежащей штанге и совпадающей с точкой В1

B 2

кулачка;

υ — скорость скольжения точки В2 штанги относительно точки B1 кулачка.

B 2 B 3

Она направлена параллельно линии ии, касательной к профилю кулачка.

План скоростей изображен на рис. 44, б. От точки р отложим отрезок pb1 перпендикулярный АВ — вектор скорости υB 1 ; через точку b1 проведем направление скорости υB 2 B 1 —линию, параллельную ии, а из полюса р линию, параллельную Ау, — направление скорости υB 2 . В пересечении этих линий найдем точку b2 — конец вектора скорости точки υB 2 . План скоростей построен. Масштаб его найдем по формулам (25) и (26).

Во избежание ошибок планы ускорений следует строить для заменяющего махенизм

ЛЕКЦИЯ ПЯТАЯ

(Продолжение четвертой лекции)

6°. Планы ускорений (планы аналогов ускорений).

Задача об ускорениях решается в той же последовательности, что и задача о скоростях. Ее решение будет основываться на соотношениях типа (11), (15) и (17). Основные свойства планов ускорений будут аналогичны основным свойствам планов скоростей.

Эти свойства следующие.

1)Векторы абсолютных ускорений всех точек механизма имеют своим началом полюс (начало) плана π.

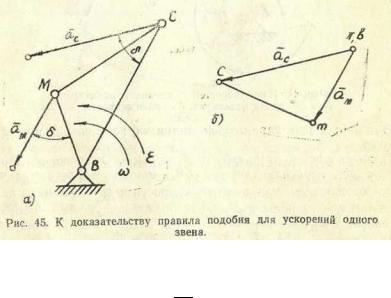
2)Правило подобия. Концы векторов абсолютных ускорений точек одного звена образуют на плане ускорений фигуру, подобную той, которую одноименные точки образовали на самом звене.

Замечание. В планах скоростей стороны подобных фигур составляют угол 90˚ (обычные планы) или параллельны (повернутые планы). В планах же ускорений эти стороны наклонены одна к другой под углом δ, который определяется формулой

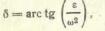(30)

ε—- угловое ускорение звена: ω — угловая скорость его.

На рис. 45, а показано звено ВСМ, вращающееся с угловой скоростью ω и угловым

ускорением ε , а на рис. 45, б построен план ускорений этого звена. Так как модули векторов а и

С

а пропор

М

циональны расстояниям ВС и ВМ, то треугольники ВМС и bmс подобны.

3)Угловые ускорения звеньев

здесь εl — угловое ускорение звена;

aj k — касательное ускорение точки j при вращении звена относительно точки k ;

lj k - расстояние между точками j и k

4)Масштабы планов ускорений и их аналогов связаны соотношением:

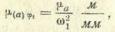(32)

где µa — масштаб плана ускорений;

µ( a ) φ1— масштаб плана аналогов ускорений;

ω1 — угловая скорость ведущего звена.

Построение планов ускорений для групп Ассура второго класса проследим на примерах построения их для отдельных механизмов. Будем считать, что для всех механизмов известны: размерные параметры, ведущее звено (ему будем приписывать номер один), положение ведущего звена (оно задано углом φ1), угловая скорость ω1 ведущего звена (она считается постоянной).

Кроме того, для этих механизмов задачи о положениях и скоростях решены.

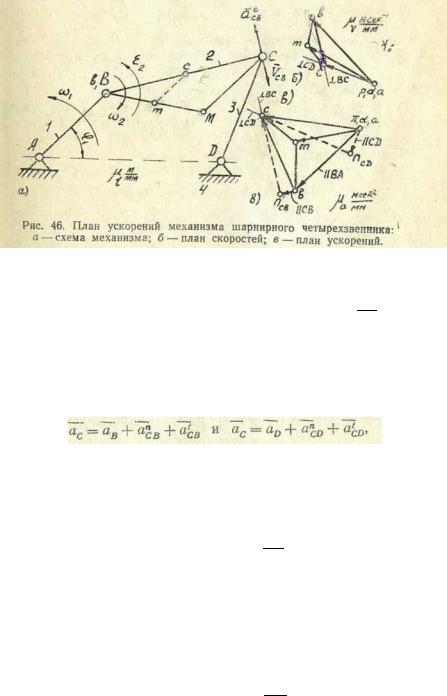
Пример 1. Дан механизм шарнирного четырехзвенника (рис. 46, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, первого вида (звенья

2 и 3)

Решение. Задача о положениях решена (рис. 46, а), также решена задача о скоростях: построен план скоростей (рис. 46, б)

υ2

Строим план ускорений. Ускорение центра шарнира В, аВ = B

lAB

и направлено параллельно ВА, ускорение центра шарнира D равно нулю: aD =0. Имея в виду соотношение (11), можно утверждать, что, определив ускорение центра шарнира С, решим задачу об ускорениях для группы BCD (так как мы будем знать ускорения двух точек каждого звена группы).

Напишем формулу типа (17) для звена 2 и звена 3:

где a —ускорение центра шарнира С;

С

а — нормальное ускорение центра шарнира В, оно же будет» и полным

B

ускорением его, так как звено 1 вращается; равномерно;anCB — нормальное ускорение центра шарнира С при вращении

υ2

звена 2 около центра шарнира В, anCB = CB и направлено

lCB

параллельно линии СВ от С к В;

atCB— касательное (тангенциальное) ускорение центра шарнира С, аtCB = εl2lBC и направлено перпендикулярно линии ВС;

a —ускорение центра шарнира D, оно равно нулю;

D

anCD— нормальное ускорение центра шарнира С при вращении

t — касательное ускорение центра шарнира С при вращении звена 3 около центра

aCD

шарнира D, atCD = ε3lCD и направлено перпендикулярно линии CD. Совместное решение двух равенств типа (17) и даст искомый план. От точки π начала плана откладываем отрезок πb (рис. 46, в), параллельный линии BA, он пропорционален ускорению aB

Масштаб плана ускорений

(33)

Вычисляем длину отрезка bпсв, изображающего в плане ускорение аnCB,

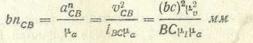(34) и откладываем его от точки b— конца вектора aB,

параллельно линии СВ: через точку nCB проводим линию, перпендикулярную линий СВ,

— направление ускорения аtCB. Теперь строим правую часть второго равенства.

От точки π следует отложить ускорение аD, оно равно нулю, поэтому конец его dφ совмещаем с точкой π (полюсом плана). От точки dφ отложим отрезок dφnCD, величину

перпендикулярную линии CD,— направление ускорения аtCD . Пересечение этой линии с ранее проведенной через точку пCB даст точку с — конец вектора искомого ускорения центра шарнира С, а сам вектор определится, если соединить точки π и с. Соединив точки b и с, получим вектор полного ускорения центра шарнира С, которое у него будет при вращении звена 2 около центра шарнира В, — ускорение аCB.

Ускорение точки М звена 2 найдем, если на стороне bс в плане построим треугольник bст, подобный треугольнику ВСМ на звене 2. Стороны треугольника bст легко определить графически. Для этого на стороне ВС (рис. 46, а) отложим отрезок bс, равный отрезку bс на плане. Проведя через точку с линию, параллельную СМ до пересечения со стороной ВМ, найдем точку т, тем самым и длины всех сторон треугольника bтс.

Угловое ускорение звена 2 определим по формуле (31):

аналогично может быть найдено угловое ускорение звена 3.

Совместив точку а с точкой π, получим не только план ускорений группы, но и план ускорений всего механизма.

В заключение укажем, что при построении планов в масштабе кривошипа значительно сокращаются все вычислительные операции. Так, если рb = АВ (на плане скоростей) и πb = АВ (на плане ускорений), то масштабы планов

Тогда, например, отрезок bпCB будет определяться так

Отсюда надо запомнить правило для нахождения отрезков в плане ускорений (при условии, что планы скоростей, и ускорений построены в масштабе кривошипа): в формулы, по которым определяются те или иные ускорения, следует вставлять не значения скоростей и длин, а отрезки из плана скоростей и плана положений, которые замеряются по чертежу. Если эти отрезки измерены в миллиметрах, то и отрезок, изображающий соответствующее ускорение, будет измеряться в миллиметрах.

Пример 2. Дан кривошипно-шатунный (ползунный) механизм (рис. 47, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, второго вида (звенья 2 и 3).

Решение. Задача о положениях решена (рис. 47, а), также решена задача о скоростях: построен план скоростей (рис. 47,6). Строим план ускорений. Ускорение центра шарнира

υ2

В известно: aB = B , направлено параллельно линии ВА. Угловое ускорение звена 3

lAB

равно нулю. Имея в виду соотношение (11), можно утверждать, что, определив ускорение центра шарнира С, мы решим задачу об ускорениях для группы, состоящей из звеньев 2 и 3 (так как мы будем знать для звена 2 ускорения двух точек, а для звена 3 — ускорение одной точки и угловое ускорение звена). •

Напишем формулу типа (17) для звена 2:

где ас —ускорение центра шарнира С, его величина неизвестна, а направлено оно параллельно линии хх;

υ2

ав— ускорение центра шарнира В, ав = B и направлено

lAB

параллельно линии ВА от В к А

anCB - нормальное ускорение центра шарнира С при вращении

υ2

звена 2 около центра шарнира В, апCB = CB и направлено

lCB

параллельно СВ от С к В;

atCB — касательное ускорение той же точки в том же движении, оно направлено перпендикулярно линии ВС.

Решение равенства типа (17) даст искомый план. От точки π начала (полюса) плана откладываем отрезок πb (рис. 47, в), параллельный линии ВА, он пропорционален

ускорению аB.

Вычисляем масштаб плана по формуле (33):

Вычисляем длину отрезка bпCB, изображающего в плане ускорение аnCB, по формуле (34):

и откладываем его от точки b — конца вектора аB, параллельно линии СВ, через точку пCB проводим линию, перпендикулярную линии ВС, — направление ускорения аtCB. Через начало плана проводим линию, параллельную линии хх, — направление ускорения аC. В пересечении этой линии с перпендикуляром к ВС найдется точка с — конец вектора

ускорения аC.

В полюс плана поставим точку а и тем самым получим план ускорений всего механизма. Угловую скорость и угловое ускорение шатуна (звена 2) можно найти по формулам (27) и (31).

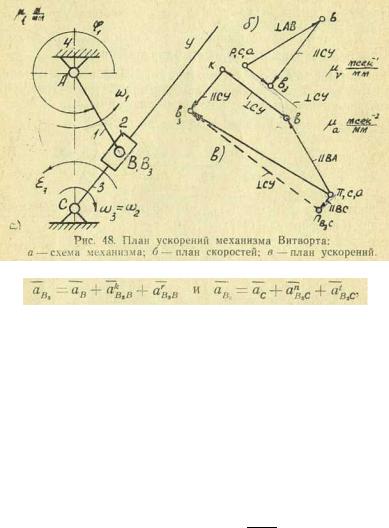
Пример 3. Дан механизм Витворта (рис. 48, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, третьего вида (звенья 2 и 3).

Решение. Задача о положениях решена (рис. 48, а), также решена задача о скоростях: построен план скоростей (рис. 48,6).

Строим план ускорений. Ускорение центра шарнира В известно: aB = ω12l AB и направлено параллельно линии ВА. Угловые ускорения звеньев 2 и 3 одинаковые (неизвестные). Ускорение центра шарнира С равно нулю. Найдя ускорение точки В3, лежащей под центром шарнира В, мы задачу решим, так как для звена 3 будут известны ускорения двух точек (следовательно, и угловое ускорение его), а для звена 2 известны ускорение одной точки и угловое ускорение звена.

Для точки В3 напишем уравнение типа (15) и (17)

где аB3— ускорение точки В3

аB — ускорение центра шарнира В , а B = ω12l AB и направлено параллельно линии ВА akB3B — ускорение Кориолиса в движении точки В3 относительно центра шарнира В,

akB3B = 2 ω2 υB3B и направлено перпендикулярно линии С у (направление ускорения Кориолиса легко определить, если повернуть вектор относительной скорости υ B 3 B на 90° по направлению угловой скорости звена 2);

arB3B - ускорение относительное (релятивное) в движении точки В3 относительно центра шарнира В, оно направлено параллельно линии Су;

ас — ускорение центра шарнира С, ас = 0;

anB3C — ускорение нормальное точки В3 при вращении звена 3

υ2

около центра шарнира С. anB3C = B3 C и направлено

lBC

параллельно Су

atB3C — ускорение, касательное точки В3 в том же движении звена 3, аtВ3С = εl3lBC и направлено перпендикулярно линии Су.

Совместное решение равенств типа (15) и (17) даст искомый план. От точки π

— начала плана откладываем отрезок πb (рис. 48, в), параллельный линии ВА, он пропорционален ускорению аВ.

Вычисляем масштаб плана ускорений по формуле (33):

Вычисляем длину отрезка bk, изображающего в плане ускорений, ускорение Кориолиса аkB3B:

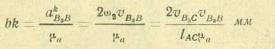(35)

иоткладываем его от точки b перпендикулярно линии Су (звено 2 вращается по

часовой стрелке (рис. 48, а), вектор относительной скорости υB3B направлен параллельно линии Су (рис. 48,6). поворот его на 90° указывает направление ускорения Кориолиса). Через точку к конца вектора ускорения Кориолиса

проводим направление ускорения аrB3B параллельно линии Су. Откладываем вектор ускорения центра шарнира С; так как это ускорение равно пулю, то его конец

оказывается в начале плана, в точке л. Вычисляем длину отрезка πnB3C по формуле (34) (отрезок пропорционален а пB3C)

иоткладываем его от точки с — конца вектора ускорения центра шарнира С

(ускорение аC равно нулю, поэтому его конец оказался в начале плана π). Через точку пB3C проводим линию, перпендикулярную линии Су, — направление ускорения аt B 3 C . Пересечение этой линии с ранее проведенной через точку k даст точку b3 — конец вектора ускорения точки В3. Совместив точку а с началом плана π, получим план ускорения механизма. Угловое ускорение звена 3 можно найти по формуле (31):

Пример 4. Дан кривошипный механизм с качающимся ползуном (рис. 49, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, третьего вида (звенья 2 и 3).

Решение. Задача о положениях решена (рис. 49, a), также решена задача о скоростях: построен план скоростей (рис. 49,6). Строим план ускорений. Ускорение центра шарнира В известно: aB = ω12lAB, оно направлено параллельно линии ВА. Угловые ускорения звеньев 2 и 3 одинаковые (неизвестные). Ускорение центра шарнира С равно нулю. Найдя ускорение точки С2, лежащей под центром шарнира С и принадлежащей звену 2, мы задачу решим, так как для звена 2 будут известны ускорения двух точек, а следовательно, и его угловое ускорение и для звена 3 известны угловое ускорение и ускорение одной точки—центра шарнира С (равное нулю).

Для точки С2 напишем уравнения типа (15) и (17):

параллельно линии ВА;

an — нормальное ускорение точки С2 при вращении звена 2

C 2 B

направлено перпендикулярно линии ВС.

Совместное решение равенств типа (15) и (17) даст искомый план. Начнем построение плана с правой части равенства типа (17). От точки я начала плана откладываем вектор ускорения аB — отрезок πb.

Вычисляем масштаб плана ускорений по формуле (33):

Вычисляем длину отрезка bпC2B, соответствующего ускорению aпC2B, по формуле (34)

и откладываем его от точки b параллельно линии СВ, через точку nC2B проводим направление ускорения atC2B — линию, перпендикулярную ВС.

Строим правую часть равенства типа (15). От точки я откладываем вектор πk — ускорение akC2C, его величину (длину отрезка) найдем по формуле (35):

Из конца вектора akC2C —точки k проведем линию, параллельную СВ — направление ускорения апC2C. Пересечение этой линии с ранее проведенной через точку пC2B даст точку с2 — конец вектора искомого ускорения точки С2. Угловое ускорение звена 2, а следовательно, и 3 найдем по формуле (31):

Для получения плана ускорений механизма в точку я поместим точку π, отображающую коней ускорения центра шарнира А.

Пример 5. Дан механизм машины для насечки пил (рис. 50, а). Этот механизм образован присоединением к ведущему звену 1 группы Ассура второго класса, второго вида (звенья 2 и 3) и группы Ассура второго класса, четвертого вида (звенья 4 и 5), которая присоединена к группе второго вида.

Решение. Задача о положениях решена (рис. 50, а), также решена задача о скоростях: план скоростей построен (рис. 50,6).

Строим план ускорений. Его надо строить по группам Ассура, начиная с той, которая присоединена к ведущему звену, это группа второго класса, второго вида (звенья 2 и 5). Для этой группы план ускорений мы строить умеем. Этот план построен (рис. 50, б) — многоугольник πbnCBс (см. пример 2 этой лекции). Для группы второго класса четвертого вида (звенья 4 и 5) мы знаем угловое ускорение звена 4, оно равно угловому ускорению звена 2, которое определяется из плана ускорений группы второго класса, второго вида. Для решения задачи достаточно найти ускорение центра шарнира D, так как для звена 4 будут известны ускорение одной точки и угловое ускорение звена; для звена 5 достаточно знать ускорение одной точки, звено движется поступательно. Для точки D — центра шарнира — напишем равенство типа (15):

Графическое решение равенства типа (15) (рис. 50, в).

От точки dφ2 отложено ускорение akDD2 отрезком dφ2k, его величина найдена по формуле (35):

Через точку k проведена линия, параллельная ВС,— направление ускорения a r DD2 и из начала плана π— линия, параллельная Dy, — направление aD. Точка dφ пересечения этих линий дает конец вектора искомого ускорения aD . Помещаем в полюс плана точку а, отображающую конец вектора ускорения центра шарнира А. На рис. 50, в показан план ускорения двух групп Ассура второго класса и ведущего звена, т. е. план ускорения всего механизма.