
Учебные пособия / Эдельштейн лекции по ТММ учебник
.pdf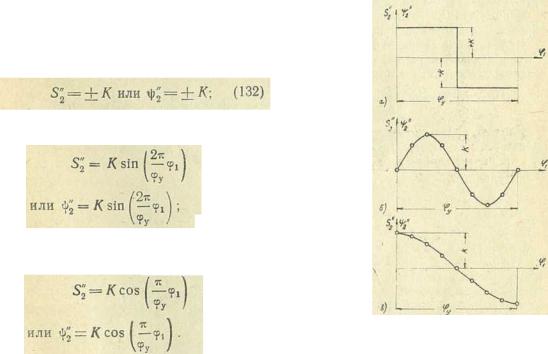
Наиболее характерные графики второй производной от функции положения штанги показаны на рис. 136:
а) вторая производная постоянна (рис. 136, а)
б) вторая производная изменяется по закону синуса (рис. 136, б )
(132 а)
в) вторая производная изменяется по закону косинуса (рис. 136, в)
(132 б)
Рис. 136. Типы второй производной от функции положения штанги:
а - постоянная величина; б - изменяется по закону синуса; в-изменяется по закону косинуса.
Для нахождения значения функции положения дважды интегрируют заданную вторую производную. При интегрировании учитывают следующие начальные и граничные
условия: при φ1=0S'2 = 0 и при φ1=φyS2=S2max, соответственно при φ1=0 ψ'2=0ипри φ1=φy,
ψ2=ψ2max .
Задавать движение штанги второй производной от функции положения ее целесообразно потому, что мы тем самым задаем ускорения штанги. Для штанги, движущейся поступательно, ее ускорение по формуле (22) а2 =S''2ω21 , а для вращающейся поформуле (23) ɛ2 = ψ̍'2ω21 .
По известному ускорению штанги всегда может быть подсчитано ее инерционная нагрузка |Ри2 | = т2а2 или |Ми2| = I2ɛ2 и найдено динамическое воздействие штанги на кулачок.
3°. Проектирование профиля кулачка — графическое решение (решение будет рассмотрено только для фазы удаления).
Для всех кулачковых механизмов применим универсальный прием проектирования — метод обращения движения. Этот метод заключается в том, что всему механизму сообщают скорость обратную по знаку скорости кулачка. Тогда кулачок, как бы остано - вится, а стойка вместе со штангой начинает двигаться относительно кулачка (штанга относительно стойки сохраняет свое движение, определяемое функцией положения).
Профилем кулачка будет огибающая всех положений элемента кинематической пары четвертого класса на штанге в этом относительном движении.
Проектирование профиля кулачка типа I, ас роликом
на штанге (рис. 137)
Дана функция положения S2 = S2(φ1) (рис. 137, а), кулачок вращается равномерно по стрелке часов. Известны: радиус ролика Rрол и наикратчайшее расстояние от центра ролика В до центра вала кулачка А — Rmin.
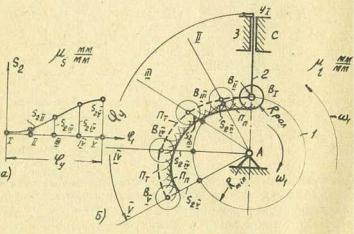
Рис. 137. Синтез кулачкового механизма типа 1-а с роликом на штанге:
а — функция положения штанги; б — образование профиля
кулачка.
Строим механизм в положении АВ1Y1, когда центр ролика В1находится в наикратчайшем расстоянии от центраА вращения кулачка 1 (рис. 137, б). Проводим окружность радиуса Rmin. Будем сначала строить теоретический профиль кулачка ПТПТ, т. е. такой, когда на штанге 2 будет острие, совпадающее с центром ролика В. Обращаем движение. Кулачок «остановился», а осевая линия АY1 вращается около центраА с угловой скоростью ω1 При повороте кулачка на фазовый угол φу осевая линия AY1повернется тоже на этот же угол φу (относительно кулачка) и займет положение AV.
Делим фазовый угол на графике S2 = S2(φ1) (рис. 137, а)и на чертеже (рис. 137,6) на т равных частей (в нашем случае на 4). Находим по графику S2 = S2(φ1) перемещения штанги ординаты, отвечающие каждому положению механизма, S2II, S2IIIи т. д.
От окружности радиуса Rminоткладываем эти перемещения вдоль линий A II, AIII, A IV и A V и тем самым находим положения центра ролика, которые он займет вследствие скольжения штанги 2 вдоль направляющих поступательной кинематической пары С
(положения BII, BIII…).
Огибающая всех положений центра роликаВ даст искомый теоретический профиль ПТПТ кулачка. Практический профиль ППППнайдется, как огибающая всех положений ролика.
Проектирование профиля кулачка типа I, а а а старелкой хх
на штанге (рис. 138
Дана функция положения штанги S2 = S2(φ1) (рис. 138, а), кулачок вращается равномерно по стрелке часов. Известно кратчайшее расстояние от центра А вала кулачка
до тарелки хх — Rmin
Строим положение механизма AB1Y1 когда тарелка хх отстоит от тентраА вала кулачка на расстоянии, равном Rmin.Проводим окружность радиуса Rmin. Обращаем движение. Кулачок «остановился», а осевая линия AY1вращается около центраА с угловой скоростью ω1. При повороте кулачка на фазовый угол φ y осевая линия AY1(относительно кулачка) тоже повернется на этот же угол φyи займет положениеА V.
Делим фазовый угол на графике S2 = S2(φ1) (рис. 138, а)и на чертеже (рис. 138,6) на mравных частей (в нашем случае на 4). Находим по графику S2 = S2(φ1)перемещения штанги, отвечающие, каждому положению механизма, ординаты: S2II, S2IIIи т. д.
От окружности радиуса Rmin откладываем эти перемещения вдоль линий А II, AIII, А
IV й А V и тем самым находим положения тарелки хIIхII, |
хIIIхIII(эти |
положения |
перпендикулярны соответствующим линиям .AY), которые она займет при перемещении |
||
штанги 2 вдоль направляющих поступательной кинематической пары |
С. Огибающая |
|
ПТПТ |
|
|
всех положений тарелки будет искомым профилем кулачка. |
|
|

Рис. 138. Синтез кулачкового механизма типа 1-а с тарелкой на штанге:
а — функция положения штанги; б — образование профиля
кулачка.
Проектирование профиля кулачка типа I, б с роликом
на штанге (рис. 139)
Дана функция положения штанги ψ2=ψ2(φ1)(рис. 139, а), кулачок вращается равномерно по стрелке часов. Известны: радиус ролика Rрол,расстояние между центрами вращения кулачка и штанги lАС длина штанги lBC (может быть задан начальный угол ψ0 отклонения штанги от линии центров АС) и кратчайшее расстояние от центра ролика В до центра вращения кулачка Rmin.
Строим положение механизма AB1C1,когда центр ролика находится в наикратчайшем расстоянии от центра вращения кулачка. Проводим окружность радиуса Rmia.
Обращаем движение. Кулачок «остановился», а линия центров АС вращается около центраА
c угловой скоростью —ω1.При повороте кулачка на фазовый угол φyлиния центров AC1(относительно кулачка)тоже повернется на этот же угол и займет положение AСv.
Делим фазовый угол φy на графике ψ2=ψ2(φ1)(рис. 139, а) и на чертеже (рис. 139, б) на т равных частей (в нашем случае на 4) и находим положения центра вращения штанги для каждого положения механизма — точки СIСII, СIII ... Из этих точек, как из центров, засекаем окружность радиуса Rm i n дугами окружностей радиуса lвс—находим начальные
положения штанги (C1 B, СI I В, СI I I В,CIVB, СV В). По графику ψ2=ψ2(φ1)находим углы поворота штанги 2 (ψ2II = y2II·µф , ψ2ШII = y2IШI·µф….) Для соответствующих
положений механизма откладываем эти углы от начальных позиций штанги и находим положения центра ролика (ВI ВI I , ВI I I ..)
Рис. 139. Синтез кулачкового механизма типа 1-6 с роликом на штанге:
а — функция положения штанги; б — образование профиля кулачка.
Огибающая всех положений центра ролика будет искомым теоретическим профилем ПТПТ кулачка. Огибающая всех положений ролика линия П П П П будет практическим профилем кулачка.
4°. Определение радиуса ролика Rр о л , минимального радиуса R m in, точек контакта тарелки с профилем
кулачка и радиуса тарелки RT .
Радиус ролика не должен быть больше наименьшего радиуса кривизны теоретического профиля кулачка на его выпуклой части:
 (133)
(133)
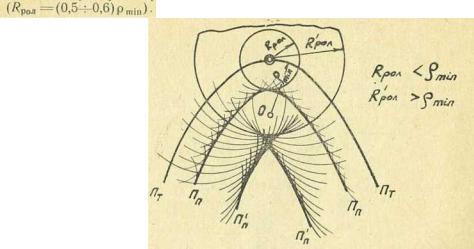
Из рис. 140видно, что если радиус ролика больше наименьшего радиуса кривизны профиля кулачка ( Ŕр о л >ωρmin),то наступает явление самопересечения огибающей, а это недопустимо. Обычно для радиуса ролика назначают размер, равный 0,5 или 0,6 от минимального радиуса кривизны теоретического профиля кулачка
Рис. 140. К определению размера радиуса ролика.
Минимальный радиус кулачка в первую очередь зависит от способов изготовления кулачка — отдельно от вала или заодно с ним и от размера самого вала кулачка. При изготовлении кулачка отдельно от вала размер минимального радиуса (рис. 141, а):
 (134
(134
где DBT—диаметр втулки кулачка, равный 1,8—2,0 диаметра вала кулачка dφB; Rрол — радиус ролика;
∆— минимальное возвышение профиля кулачка над поверхностью втулки, оно
назначается от 0,5 до 2.0 мм в зависимости от способа обработки втулки. При изготовлении кулачка вместе с валом минимальный радиус (рис. 141,6)
 (134 a)
(134 a)
здесь dφB — диаметр вала кулачка;
∆ — минимальное возвышение профиля кулачка над поверхностью вала.
Для кулачков с роликом на штанге иногда требуют, чтобы минимальный радиус был подобран так, чтобы угол давления во
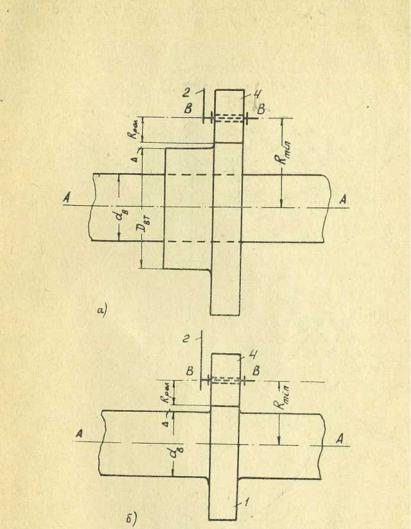
Рис. 141. к определению размера минимального радиуса кулачка:
а — при изготовлении кулачка отдельно от вала; б при изготовлении кулачка вместе с валом.
всех положениях механизма был бы равен или меньше заданного:
αmax(α≤ αmax)- При этом, конечно, должны выполняться условия(134) или (134 а).
На рис. 142 показан теоретический профиль кулачка ПТПТ, указано j-е положение механизма в обращенном движении. Для
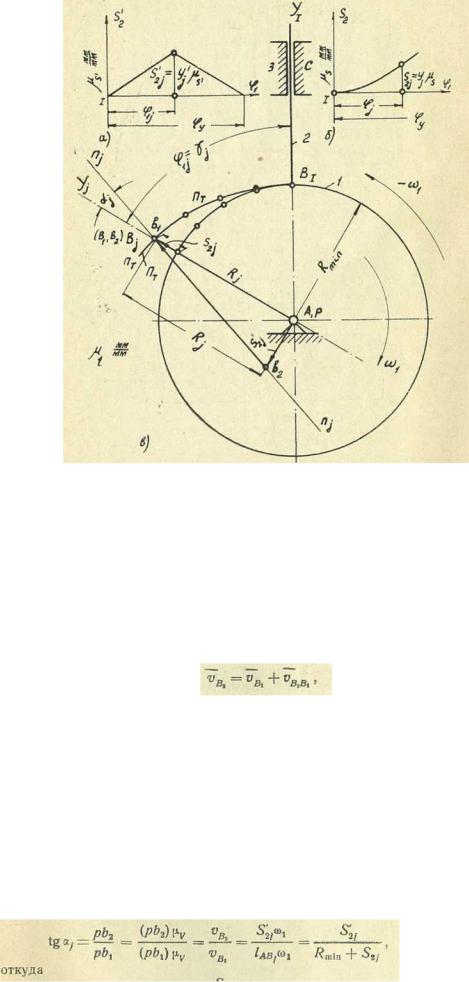
Рис. 142. К выводу зависимости минимального радиуса кулачка от угла давления:
a— график первой производной от функции положения штанги;
б — график функции положения штанги; в — повернутый план скоростей, построенный на схеме механизма.
этого положения мы знаем значение первой производной S'2lот функции положения (рис. 142 а) и значение перемещения S2j. штанги, которое определяется по графику функции положения (рис. 142,6)
Угол давления αj- будет образован направлениями нормали пj пj , к теоретическому профилю кулачка и скорости штанги для выбранного положения механизма (рис. 142, в).
Найдем связь между углом давления и минимальным радиусом кулачка. Для положения j скорость точки В2 , принадлежащей штанге, связана со скоростью точки В1 принадлежащей кулачку, следующим соотношением:
где υB2 - скорость точки В2 , υB2 = S'2jω1 и направлена параллельно линии AYj;
υB1 - скорость точки В1, υB1 = LA B ω1и направлена перпендикулярно линии ABj;
υB2B1 - относительная скорость точки В2 относительно точки В1, она направлена
перпендикулярно нормали пj пj к профилю кулачка (по касательной к профилю). Построим повернутый план скоростей непосредственно на схеме механизма (рис.
142, в). Полюс плана р совместим с центром шарнира А. Скорость точки B1 изобразим отрезком p b 1 = АВj ., а скорость точки В2 в том же масштабе — отрезком pb2, перпендикулярным линии AYj . Скорость точки В2 относительно точки В 1 будет представлена отрезком b2 b1 , по направлению этот отрезок совпадает с направлением нормали пj пj к профилю кулачка. Следовательно, угол Аb1 b2 будет углом αj давления в этом положении механизма.
Из треугольника pb1 b2 получаем

(135)
Задаваясь amaxи тем самым зная tgamax, находим для всех положений механизма допускаемые значения минимального радиуса Rm i n . Из этих значений выбираем наибольшее и принимаем его к исполнению. При этом во всех положениях механизма угол давления будет меньше или в крайнем случае равен заданномуαmax(α≤ αmax).
Для кулачков типа I, а с тарелкой на штанге при назначении размера минимального радиуса надо иметь в виду, что профиль кулачка обязательно должен быть выпуклым. В работе профессораГеронимуса показано, что это условие всегда будет удовлетворяться следующим соотношением:
(136)
здесь | —S''2max| —наибольшая по абсолютному значению отрицательная вторая производная от функции положения штанги.
Построение огибающей к тарелке по точкам и определение радиуса тарелки R Т (кулачковый механизм типа I, а а с тарелкой на штанге)
На рис. 143, в показано j-е положение механизма в обращенном движении. Для штанги известны графики: первой производной от
Рис. 143. К определению точки касания профиля кулачка с тарелкой:
а— график первой производной от функции положения штанги;
б— график функции положения штанги; в — повернутый план скоростей,
построенный на схеме механизма.
функции положения (рис. 143, а) и самой функции положения (рис.143, б )
Значение первой производной от функции положения

и самой функции
Построим план |
скоростей для j-го положения по равенству |
||
где |
B 2 = S |
'2j |
ω1 — скорость точки В2 штанги, направлена |
|
υ |
|
|
параллельно линии AYj ;
в повернутом плане - перпендикулярно ей);
υ = lA B j ω1 —скорость точки В1 кулачка, направлена перпендикулярно лини bABj (в
B 1
повернутом плане параллельно ABj );
υ — скорость скольжения точки В2 по точке В1 направлена параллельно тарелке
B 1 B 2
х j х j (в повернутом плане — перпендикулярно х j х j ). Повернутый план скоростей построен непосредственно на схеме механизма в
масштабе радиуса (рис. 143, в), поэтому p b 1 = А В j . (полюс плана р совмещен с центром шарнира А). Отрезок pb1 соответствует скорости υ B 1 , pb2 — скорости υB 2 , b2 b1 —скорости υB 2 B 1 , а отрезок Kj Bj = pb2 .Расстояние lT j от линии AYj . до точки касания Вj тарелки с профилем, взятое в натуральную величину, будет
Вычислим длину
но
(рис. 143, а), а
поэтому
откуда расстояние oтоси AYjдо
точки контакта тарелки с профилем кулачка
(137)
Очевидно, что радиус тарелки следует назначить немногим более (во избежание работы тарелки ее углом) максимального значения первой производной от функции положения штанги:
 (137 a)
(137 a)
5°. Формулы для подсчета полярных координат точек профиля кулачка (рассматриваются только кулачки типа I,а с острием и тарелкой на штанге) (рис. 142, в и 143, в).
Начало координат взято в центре шарнираА, ось отсчета — AY1 .
Для кулачкового механизма с острием на штанге (рис. 142, в) полярные координаты: радиус-вектор
 (138)
(138)
S2 находят по графику S2 = S2(φ1) (рис. 142,6), полярный угол (профильный угол)

 (138 a)
(138 a)
Для кулачкового механизма с тарелкой на штанге (рис. 143, в) полярные координаты: радиус-вектор
(139)
S2 j находят по графику S2 ≠ S2 (φ1) (рис. 143, б),aS'2 j — по графику S'2 = S'2 (φ1) (рис. 143, а), полярный угол (профильный угол)
(139 a)
угол δjjопределяют из формулы
(139 б)
6°. Примеры проектирования кулачковых механизмов.
Пример 1. Требуется спроектировать кулачковый механизм, у которого штанга движется поступательно. Осевая линия штанги проходит через центр вращения кулачка. На конце штанги имеется круглый ролик.
Начальные данные:
а) угловая скорость кулачка ω1= 100 сек- 1 вторая производная от функции положения штанги S"2 = ±K (на фазе удаления) и S"2=±К (на фазе приближения); максимальный ход штанги S2max= 10 мм;фазовые углы: удаления φу = 120°, верхней остановки φво = 30°, приближения φп = 120°, нижней остановки φно = 90°
б) радиус ролика Rpoл— 10 мм, диаметр вала кулачка dφв=25 мм; кулачок отковывается заодно с валом; минимальное возвышение профиля кулачка над поверхностью вала ∆ = 1,5 мм.
Профиль кулачка должен быть построен по 9 точкам для каждой фазы его угла поворота.
Решение. 1. Определяем функцию положения штанги S2 = S2(φ1) (графическое решение). На рис. 144,а дан график второй производной от функции положения штанги: S"2=S"2(φ1). (Ввиду сим-

Рис. 144. Закон движения штанги, заданный второй производной от функции положения штанги:
а— график второй производной; б — график первой производной;
в— функция положения штанги.
метричности цикла движения штанги функцию положения S2 = S2(φ1) находим только для фазы удаления.)
График первой производной, очевидно, имеет вид, показанный на рис. 144,6, поэтому
График S'2=S2(φ1) (рис. 144,6) делим на треугольники так, как это показано на рисунке. Площадь треугольника I—II—II укладывается в площади треугольника I—V —IX 32 раза. Следовательно, «цена» площади F1-II соответствует 1/32 максимального хода штанги S2.max(вся площадь треугольника I—V—IX отвечает значению S2max). Вычисление ординат графика S2(φ1) сведется к подсчету их по формуле
Гдеnj - число площадок F1-II, заключенных между началом координат графика S'2 (φ1) и jположением кулачка.
Результаты подсчета сведены в таблицу. |
|
|
|
|||||
|
Номера |
|
S2.maxММ |
|
|
п |
|
S2мм |
|
|
|
|
|||||
|
положений |
|
|
|
|
|
|
|
|
I |
|
10/32 |
|
|
0 |
|
0,0 |
|
II |
|
То же |
|
|
1 |
|
10/32 = 0,7 |
|
III |
|
* |
|
|
4 |
|
40/32= 1,25 |
|
IV |
|
* |
|
|
9 |
|
90/32 = 2,8 |
|
V |
|
* |
|
|
16 |
|
100/32 = 5,0 |
|
VI |
|
|
|
23 |
|
230/32 = 7,2 |
|
|
|
* |
|
|
|
|||
|
VII |
|
|
|
|
28 |
|
280/32 = 8,75 |
|
VIII |
|
* |
|
|
31 |
|
310/32 = 9,3 |
|
IX |
|
|
|
32 |
|
320/32 = 10,0 |
|
|
|
* |
|
|
|
|||
По данным четвертой графы |
|
|
|
|
|
|
||
|
таблицы построен график S2(φ1) (рис. 144, в). |
|||||||
2. Определяем минимальный радиус кулачка: |
|
|
|
|||||
