Учебные пособия / Эдельштейн лекции по ТММ учебник

ЛЕКЦИЯ ПЕРВАЯ

ВВЕДЕНИЕ

Изучение курса следует начинать с объектов, которым посвящен курс, и с его содержанием (программой).

Втеории механизмов и машин предмет изучения — механизмы и машины. Механизм

—это механическая система, состоящая из подвижно соединенных твердых или упругих тел. Эта система обладает вполне определенным движением своих частей и назначена для передачи или преобразования движения. Механизмы составляют основу всякой машины. Машина — это механизм или группа их, предназначенная для передачи или преобразования работы (энергии). Поэтому механизмы не только выполняют кинематические функции, но и служат трансформаторами усилий (сил или моментов).

Машины в основном можно подразделить на двигатели и на рабочие машины. Двигатели и рабочие машины работают в едином комплексе. Выходные валы двигателей делают быстроходными (в этом случае при заданной мощности крутящий момент на валу будет меньше, нежели у тихоходного вала). Входные валы рабочих машин имеют, как правило, скорости меньшие, чем выходные валы двигателей.

Для преобразования скорости и крутящего момента на валу двигателя в желательные скорость и крутящий момент на валу рабочей машины между двигателем и рабочей машиной ставят либо редуктор, либо коробку скоростей, либо вариатор. Редуктор — механизм для преобразования угловой скорости (из большей в меньшую); отношение скоростей в редукторе постоянно. В коробке скоростей это отношение можно изменять ступенчато, а в вариаторе— плавно.

Совокупность двигателя, редуктора (коробки скоростей, вариатора) и рабочей машины называется машинным агрегатом.

Из сказанного вытекает, что первичным предметом изучения будет механизм. Теория механизмов излагается в пяти следующих разделах:

1.Структурный анализ и классификация механизмов.

2.Кинематический анализ механизмов.

3.Силовой анализ механизмов.

4.Динамический анализ механизмов.

5.Синтез (кинематическое проектирование) механизмов.

Пр и м е ч а н и е . Из методических соображений III и IV разделы иногда меняют местами, что

ибудет сделано в нашем изложении.

Программа, методические указания, порядок прохождения курса и рекомендованная литература приведены в методическом пособии: «Программа, контрольные работы и методические указания по курсу „Теория механизмов и машин”». Под ред. Эдельштейна Б. В. МАИ, 1966.

Те м а I. СТРУКТУРНЫЙ АНАЛИЗ

ИКЛАССИФИКАЦИЯ МЕХАНИЗМОВ

§ 1. Структура механизмов

1°. Здесь даны определения составных частей механизмов и указан принцип их образования. Это можно сделать потому, что все механизмы построены идентично. Ознакомимся с понятиями и определениями.

Деталь — часть механизма, изготовленная без приемов сборки.

Звено — жестко связанная группа деталей. Например, коленчатый вал или вал с жестко насаженным на него зубчатым колесом и т. д. В механизмах звенья между собою соединяются подвижно.

Подвижное соединение двух звеньев называется кинематической парой.

Подвижно соединенные звенья образуют кинематическую цепь. Если в кинематической цепи каждое звено ее входит минимум в две кинематические пары, такая цепь называется

замкнутой.

Механизмы образуются только замкнутыми кинематическими цепями.

Для того чтобы из замкнутой кинематической цепи получить механизм, т. е. — систему определенного движения, надо: одно из звеньев предполагать неподвижным, оно

На рис. 3 показаны пары пятого класса и их условные изображения на схемах механизмов, на рис. 4 — па р а третьего класса

шаровой шарнир, на рис. 5 — пара четвертого класса (цилиндрическая). Следует помнить, что в отдельных случаях класс пары может зависеть от того механизма, в котором имеется это соединение. Например, поршень в цилиндре образует пару четвертого класса, но если эта пара имеется в плоском кривошипно-ползунном (шатунном) механизме, то ее следует отнести к пятому классу и назвать поступательной (поршень не может поворачиваться относительно продольной оси цилиндра). На этом можно закончить вопрос о структуре механизмов.

§ 2. Классификация механизмов

1°. Механизмы образуют множество, в которое входят тысячи единиц различных наименований. Так, в справочнике И. И. Артоболевского «Механизмы» приведено около 4000 различных механизмов, в справочнике Н. С. Кожевникова — 3000, а у Доброгурского — 1500. Для того чтобы разработать единые приемы их анализа и синтеза, эти механизмы разделяют на плоские, т. е. такие, у которых все звенья движутся параллельно одной и той же плоскости, и пространственные. Плоские механизмы получили большее применение в технике, поэтому их теория разработана наиболее полно. Мы будем изучать только плоские механизмы. Следует указать, что с развитием техники пространственные механизмы находят все большее применение. Развитию теории этих механизмов наука в основном обязана работам отечественных ученых. Профессор Н. И. Мерцалов впервые в мире читал курс пространственных механизмов в 1921 году на инженерном факультете Московской сельскохозяйственной Академии им. К. А. Тимирязева, а И. И. Артоболевский в 1937 г. написал монографию «Пространственные механизмы». В дальнейшем над теорией пространственных

механизмов работали: проф. Г. Г. Баранов, чл.-корр. АН СССР В. В. Добровольский, проф. Вяч. А. Зиновьев и другие.

2°. Выше было сказано, что замкнутая кинематическая цепь только тогда будет механизмом, когда число ведущих звеньев будет достаточным для сообщения ведомым определенности движения. Чтобы установить это число, применяют структурные формулы, особые для пространственных и плоских механизмов.

Формула Сомова — Малышева для пространственных механизмов, у которых нет общих для всех звеньев условий связи:

p5, p4, p3, p2, p1 — число кинематических пар соответственно пятого, четвертого, третьего, второго и первого классов.

Вывод этой формулы несложен: каждое звено в свободном состоянии обладает шестью степенями свободы, следовательно, п таких звеньев имеют 6п степеней свободы. При вхождении звена в пару пятого класса на его относительное движение накладывается пять условий связи, если число таких пар будет р4, то они наложат 5р5 условий связи. Аналогично р4 пар четвертого класса наложат 4р4 условий связи и т. д.

Разность между числом степеней свободы и числом условий связи и дает нам степень подвижности механизма, т. е. число тех независимых движений, которыми мы можем задаваться. Иначе говоря: степень подвижности механизма равна числу необходимых ведущих звеньев.

Для плоских механизмов применяется формула Чебышева

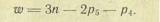(2)

Вывод этой формулы такой же, как и формулы Сомова — Малышева. Надо только иметь в виду, что в плоском движении звено имеет три степени свободы, а кинематические пары могут быть лишь пятого (вращательная или поступательная) или четвертого (высшая) классов. Пара пятого класса вносит в плоское движение звена два условия связи, пара четвертого — одно условие.

При пользовании структурными формулами предварительно надо выяснить, нет ли у всех звеньев общих для них условий связи, а затем, нет ли в механизме звеньев, вносящих пассивные связи или лишние степени свободы, эти звенья следует из расчета исключить.

Закончим лекцию чтением схем плоских механизмов и подсчетом степеней подвижности их.

На рис. 6 показано схематическое изображение звена, на рис. 7— кинематические пары. Вращательная и поступательная пары — пары пятого класса, высшая — пара четвертого класса.

Решим примеры. Условимся: звенья нумеровать арабскими цифрами, кинематические пары обозначать большими буквами латинского алфавита, число всех звеньев — k, число подвижных звеньев — п, число пар пятого класса — р5, число пар четвертого класса — р4, степень подвижности — ω.

На рис. 8 дана схема шарнирного четырехзвенного механизма, для него k =4, п =3, р5 =4, р4 =0, следовательно, ω =3 • 2—2 •4=1.

На рис. 9 дана схема кривошипно-шатунного (ползунного) механизма, для которого k = 4, п = 3, р5 = 4, р4 = 0, следовательно, ω = 3•3 — 2•4 = 1.

На рис. 10 дана схема кулисного механизма Витворта, для него k = 4, п = 3, р5 = 4, р4 = 0, следовательно, ω = 3•3 — 2•4 = 1.

На рис. 11 дана схема кулачкового механизма, для которого k = 3, п= 2, р5 = 2, р1 = l, следовательно, ω = 3•2 — 2•2 — 1 = 1.

На рис. 12 дана схема кулачкового механизма с роликом на конце штанги. Ролик в этом механизме поставлен для уменьшения трения и на кинематику штанги не влияет, поэтому его из расчета надо исключить, достаточно считать его жестко связанным со штангой.

Расчет степени подвижности для этого механизма не отличается от предыдущего примера.

На рис. 13 дана схема механизма Поселье — Липкина, для него k = 8, n = 7, р5 = 10, р4 = 0, следовательно, ω = 3•7 — 2 •1 0 = 1 . (У этого механизма в точках В, С, D, Е следует считать по две пары пятого класса, так как в них сходятся по три звена.)

ЛЕКЦИЯ ВТОРАЯ

§ 3. Классификация плоских механизмов по Ассуру — Артоболевскому

1˚. Плоские механизмы можно классифицировать по различным признакам. Поэтому для них имеется ряд классификаций. Назовем некоторые из них.

1.Разделение механизмов на механизмы с низшими парами и на механизмы с высшими и низшими парами.

2.Разделение по конструктивным признакам: шарнирно-рычажные, зубчатые, кулачковые, зубчато-рычажные и т. д.

3.По характеру воспроизводимого движения: передачи — механизмы для передачи и воспроизведения только вращательного движения и остальные (этому признаку не отвечающие).

Внашем курсе будем пользоваться в основном классификацией Ассура. Работа Петроградского профессора Л. В. Ассура относится к 1918 г. Она была продолжена в тридцатых годах академиков И. И. Артоболевским и получила свое окончательное завершение.

2°. По Ассуру — Артоболевскому класс механизма определяется строением его ведомой части. Механизмы, отнесенные к одной и той же категории (классу), имеют

общие методы кинематического и силового анализов. В этом состоит ее рациональный смысл, кроме того, как это будет показано в дальнейшем, она позволяет правильно

синтезировать новые механизмы.

По классификации Ассура — Артоболевского все механизмы образуются присоединением к системе определенного движения (ведущим звеньям и стойке) особых кинематических цепей, носящих название групп Ассура или структурных групп. Эти группы различаются своими классами: первому—присвоен номер два, последующие имеют номера три, четыре, пять и т. д. Класс механизма определяется наивысшим классом присоединенной группы. Методы кинематического и силового анализов усложняются с повышением класса механизма. В некоторых случаях удачным выбором ведущего звена класс механизма можно понизить.

Классифицировать механизмы по Ассуру — Артоболевскому можно, если соблюдены следующие условия:

1.Число ведущих звеньев равно степени подвижности механизма, это показывает, что мы имеем дело с кинематической цепью определенного движения.

2.Ведущее звено (ведущие звенья) входит в кинематическую пару пятого класса со стойкой.

3.В механизме имеются только кинематические пары пятого класса.

При наличии кинематических пар четвертого класса их следует предварительно заменить двумя парами пятого класса и одним звеном. Такая замена правомочна, так как в этом случае степень подвижности нового (заменяющего) механизма сохраняет свое значение, найденное для основного механизма, и кинематика звеньев заменяющего и основного механизмов остается одинаковой. Такая замена справедлива для трех бесконечно близких положений механизма, поэтому скорости и ускорения (первого порядка) в основном и заменяющем механизме совпадают.

Замена пар четвертого класса осуществляется так (рис. 14). В точке А контакта элементов аа и ββ пары четвертого класса проводят нормаль NN. Отмечают на этой нормали положения центров кривизны o1 и o2 элементов аа и ββ. В точках o1 и o2 помещают вращательные кинематические пары O1 и O2 и соединяют их дополнительным звеном 3. На рис. 15, а показана замена для случая, когда элементом кинематической пары четвертого класса на звене 2 будет прямая на рис. 15,6 — кривая ββ, выродившаяся в точку β, а на рис. 15, в — замена для случая, когда элементами пары, будут прямая аа и точка β.