
TM_Lectures_part_I_16
.pdf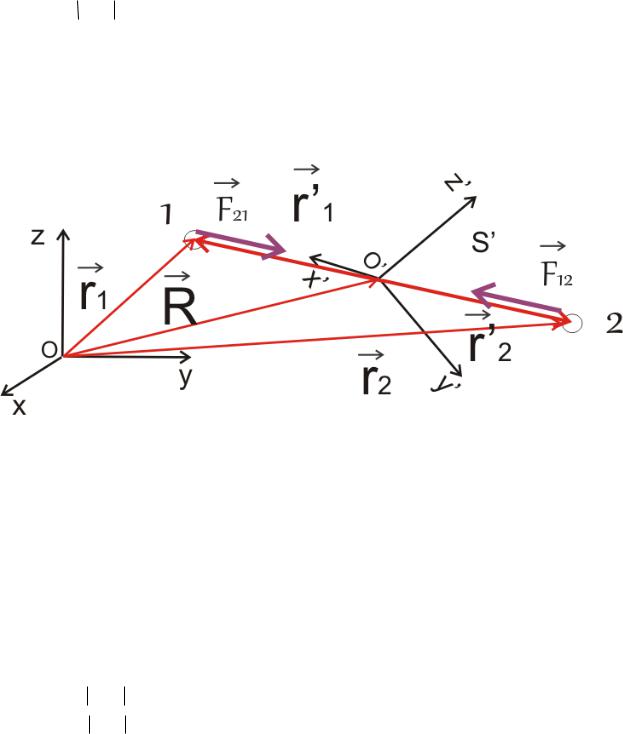
Лекция 16 (ТМ, часть I)
Задача двух тел
Рассмотрим движение двух материальных точек под действием центральной силы (при заданном потенциале взаимодействия v(r) ), то есть
|
|
|
|
-grad v r |
r |
И.С.О. F |
r |
1 |
2 |
i, j |
1 |
Поставим задачу, по заданной
, r1 t ? . r2 t ?
F
|
|
|
r |
. |
|
2 |
|
|
|
|
найти законы движения этих тел, а именно
См. рисунок
Движение этой системы подчиняется системе уравнений движения
|
|
|
|
|
F |
m r |
||
|
1 1 |
2,1 |
|
|
|
|
|
F |
m r |
||
|
2 2 |
1,2 |
(1)
Учтем, что по третьему закону Ньютона
|
|
F2,1 |
F1,2 |
Так как действующая сила потенциальная
|
|
|
|
|
|
F2,1 |
r1U r1 |
r2 |
. |
||
|
|
|
|
||
F1,2 |
r2U r1 |
r2 |
|
|
|

В данном случае, все расстояния удобно производить относительно центра
масс
|
|
r |
R |
1 |
|
R системы.
|
|
, |
|
|
|
|
|
r2 |
|
|
|||
r1 |
R r2 |
|||||
Так как система консервативна и замкнута, равнодействующая сила приложенная к центру масс равна нулю и скорость движения центра масс сохраняется
Fкул 0 VR |
const . |
Перейдем в систему центра масс, его движения в силу условий описанных выше является поступательным
|
|
(2) |
R VRt R0 |
||
Система (1) в системе центра масс приобретет следующий вид
|
|
|
|
|
|
m r F |
||
|
1 1 |
2,1 |
|
|
|
|
|
|
m r F |
||
|
2 2 |
1,2 |
(3)
При этом условие перехода к системе с центром в центре масс подразумевает выполнение следующих взаимосвязей между радиус векторами
|
|
|
|
|
, |
||
|
|
|
|
|
0 |
||
m1r1 m2r2 |
|||||||
|
|
|
|
|
|
|
|
r |
r r |
r |
r |
||||
2 |
1 |
2 |
|
1 |
|
|
|
|
|
m |
|
, |
|
|
|
r |
|
1 |
|
r |
|
|
|
|
|
|
|
||||
2 |
|
m2 |
1 |
|
|
|
|
|
|
|
|
|
|
||
m1 . m2 r1 r1 r
,
В результате получим:
|
|
|
m2 |
|
|
r1 |
|
|
|
r |
|
m1 |
m2 |
||||
|
|
(4) |
|||
|
|
m |
|||
r2 |
1 |
r |
|||
|
|
|
|
||
m1 m2
Полученная взаимосвязь позволяет перейти от систем 2х двух равнений к одному уравнению, а именно
|
|
|
|
|
|
|
|
m1m2 |
|
||||
|
|
|
|
r |
F2,1 |
|
|
|
|
||||
|
|
m1 m2 |
. |
|||
|
|
m m |
|
|
||
|
|
1 2 |
|
|
|
|
|
|
|
r F1,2 |
|||
m m |
|
|||||
|
2 |
|
|
|
||
|
|
1 |
|
|
|
|

Введем обозначение
|
m m |
||
1 |
2 |
||
|
|||
|
m m |
||
|
1 |
2 |
|
,
Которое определяет так называемую приведенную массу. С его учетом уравнение движения приобретает следующий вид
|
|
|
F |
r |
здесь
|
|
F |
|
(5),
|
|
rU |
r |
,
Если мы знаем решение уравнения (5), в лабораторной системе отсчета решение задачи приобретает следующий вид:
|
|
|
|
m |
|
t |
|
r |
t R |
2 |
r |
||
|
|
|
|
|
||
1 |
|
|
m m |
|
||
|
|
|
|
|
||
|
|
|
|
1 |
2 |
|
|
|
|
||||
|
|
m |
|
t |
||
r |
t R |
1 |
r |
|||
|
|
|
|
|
|
|
|
2 |
|
|
m m |
|
|
|
|
|
|
|||
|
|
|
|
1 |
2 |
|
. (6)
Далее решение задачи проводится в соответствии с теорией предыдущих параграфов, а именно момент импульса и энергия могут использоваться как интегралы движения.
|
|
|
|
|
|
|
|
|
|
M0 |
r 0 0 , |
|
|
||||||
|
|
|
|
|
|
|
, |
||
M0 |
r |
0 P0 |
|||||||
здесь |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
r |
0 r2,0 |
r1,0 |
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
v |
0 v2,0 |
v1,0 |
, |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
P r2 |
r1 , |
|
|
||||||
|
|
|
|
|
|
|
|||
P m r |
m r . |
||||||||
|
|
2 |
2 |
|
|
1 1 |
|
|
|
(7)
Используя законы сохранения полной энергии и момента импульса, запишем
|
|
|
V |
2 |
0 |
|
|
|
E0 |
|
|
2 |
|
V r 0 , |
|
||
|
|
|
|
|
|
|
||
|
|
2 |
|
|
2 |
V E0 |
|
|
|
2 |
|
|
(9) |
||||
|
|
|
M 0 |
|||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|

здесь
. r t t
Решение (9) нами уже было получено ранее. Выпишем решение уравнений
(9) с учетом того, что у нас тело, движение которого мы описываем имеет приведенную массу - . Для этого мы используем интегралы движения для задачи о движении тела в центрально-симметричном поле:
t |
|
|
|
|
|
d |
|
|
|
|
|
|
|
1 |
|||
|
2 |
|
|
E |
|
U |
|
|
|
C |
|||||||
|
|
|
|
|
|
eff |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
0 |
|
|
|
d |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
E |
U |
eff |
|
C2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U |
|
|
|
|
|
2 |
|
U |
|
||||||||
eff |
|
|
|
0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (10)
В заключении можно сделать следующие выводы:
1. Задача двух тел относится к точно решаемым задачам в теоретической механике.
2. Выражения (10) дают закон движения материальной точки массы в
центрально-симметричном поле.
3. Это значит, что задача двух тел сводится к задаче одного тела с массой m
в центрально-симметричном поле.
4. В системе отсчета связанной с центром масс движение тел происходит в плоскости проходящей через центр масс, а траектории движения тел подобны друг другу с центром подобия в центре масс и с коэффициентом подобия равным отношению их масс.
5. При этом движение центра масс относительно лабораторной (неподвижной)
системы отсчета происходит равномерно и поступательно.
