3. Метод средней точки

Схема алгоритма метода средней точки, представленная на рис. 2.6-3, требует дополнения процедуры-функции f(x), в которой вычисляется значение целевой функции.

Рис. 2.6-3. Алгоритм метода средней точки

Алгоритм метода средней точки [2] основан на сокращении длины текущего отрезка неопределенности [a;b], путем отбрасывания той половины отрезка, которая не содержит точки минимума. В основу метода положено основное свойство унимодальности функции, то есть, для того чтобы на отрезке [a;b] существовал минимум, необходимо, чтобы первая производная на нем была неубывающей. Выбрав середину текущего отрезка c=(a_i+b_i)/2), принимается решение: если , то в следствии унимодальности функции, точка минимума не может лежать левее точки с, переопределяется левая граница отрезка(a_i+1=с), а если , то минимум не может лежать правее точки с и переопределяется правая граница отрезка (b_i+1=c). В случае если за точку минимума принимают значение с.

Сокращение отрезка проводятся до тех пор, пока не выполнится неравенствоΔ_n=|b_n-a_n|≤ε.

После каждой итерации длина отрезка неопределенности сокращается в 2 раза, однако метод имеет существенный недостаток –необходимость вычисление производной от целевой функции.

7. Алгоритмы методов многомерной оптимизации

Итерационные методы, применяемые для решения задач минимизации функции нескольких переменных, относятся к классу методов спуска[3]. В них каждая итерация(k) приводит к уменьшению значения целевой функции: Q(x_k+1,y_k+1)<Q(x_k,y_k), для всех k³0.

В качестве начальной точка (x₀, y₀)выбирается точка, принадлежащая области допустимых значений функции.

Поскольку направление спуска совпадает с направлением вектора антиградиента, то координаты очередной точки траектории спуска вычисляются по формулам:

где l_k - шаг спуска. Способ задания шага спуска l_k определяется конкретным методом.

Итерации повторяются до тех пор пока не выполняется условие окончания цикла:

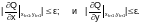
Схема алгоритма метода градиентного спуска, представленная на рис. 2.7-1, требует дополнения следующих процедур-функций:

• Q(x,y) – целевая функции;

• g1(x,y) – частная производная по х;

• g2(x,y)– частная производная по y.

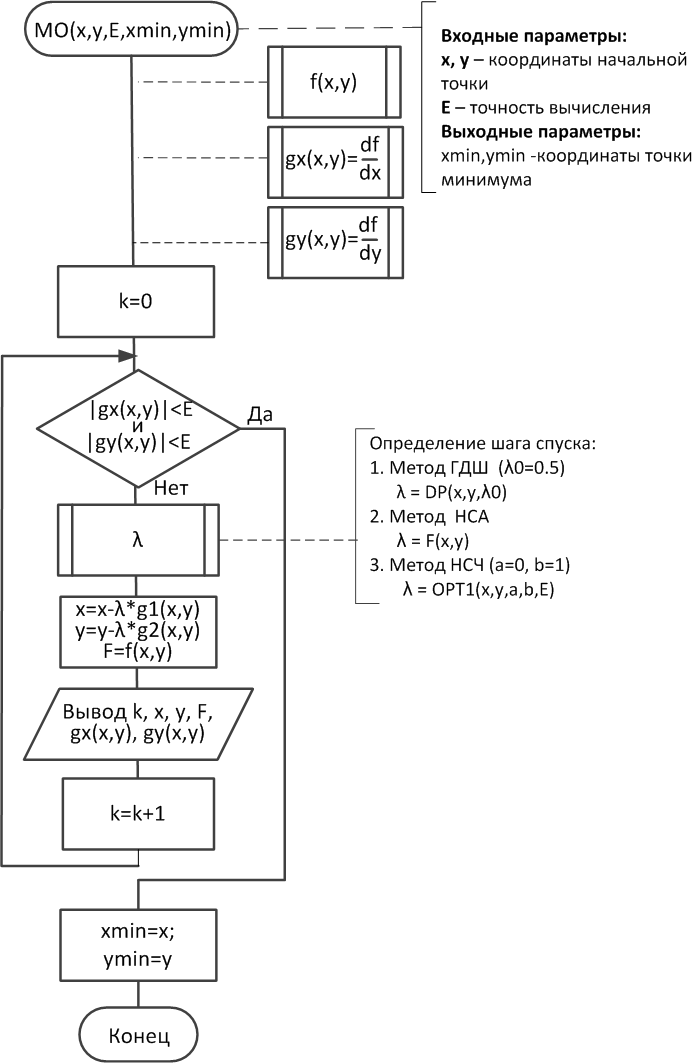
Рис.2.7-1. Алгоритм методов наискорейшего спуска

Схемы алгоритмов выбора шага спуска(λ) выбирается в зависимости от используемого метода (рис.2.7-2, рис.2.7-3).

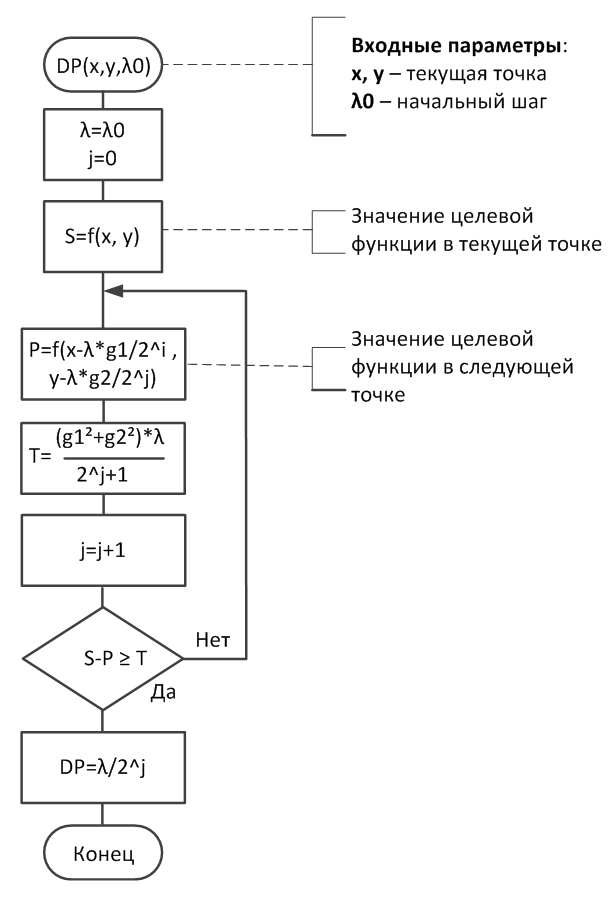
Рис. 2.7-2. Выбор шага в методе ГДШ

В методе градиентного спуска с дроблением шага выбор шага спуска осуществляется следующим образом.

Начальный шаг спуска l₀, как правило, задается равным 0,5. На каждой k-й итерации для выбора шага l_kпроизводится проверка условия:

где

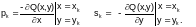
Если условие выбора шага не выполняется, то шаг полагается равным lk = lk/2 и проверка условия возобновляется. При выполнении условия выбора шага его значение передается в процедуру вычисления координат очередной точки спуска.

В методах наискорейшего спуска из выбранной точки (x₀,y₀) спуск осуществляют в направлении антиградиента до тех пор, пока не будет достигнуто минимальное значение целевой функции Q(x, y) вдоль луча, направление которого определяет вектор антиградиент.

Если выразить целевую функцию Q(x, y) через шаг l, то на определенном шаге, при фиксированных значенияхxи y, целевую функцию можно представить как функцию одной переменной:

Величина шага на каждой итерации определяется из условия минимума функции :

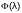= min( (l)) l_k = l*(x_k, y_k), l>0.

Таким образом, выбор шага l_k на каждой итерации предполагает решение задачи одномерной оптимизации. По способу решения этой задачи различают два метода наискорейшего спуска [3]:

• аналитический метод (НСА);

• численный метод (НСЧ).

В методе НСА[3] формулу для вычисления значения текущего шага спуска получают аналитически перед компьютерной реализацией алгоритма из условия .

В методе НСЧ величину l_k находят на отрезке [0;1] c заданной точностью, используя один из методов одномерной оптимизации, например, метода золотого сечения (рис. 2.7-3). В качестве целевой функции используется .

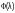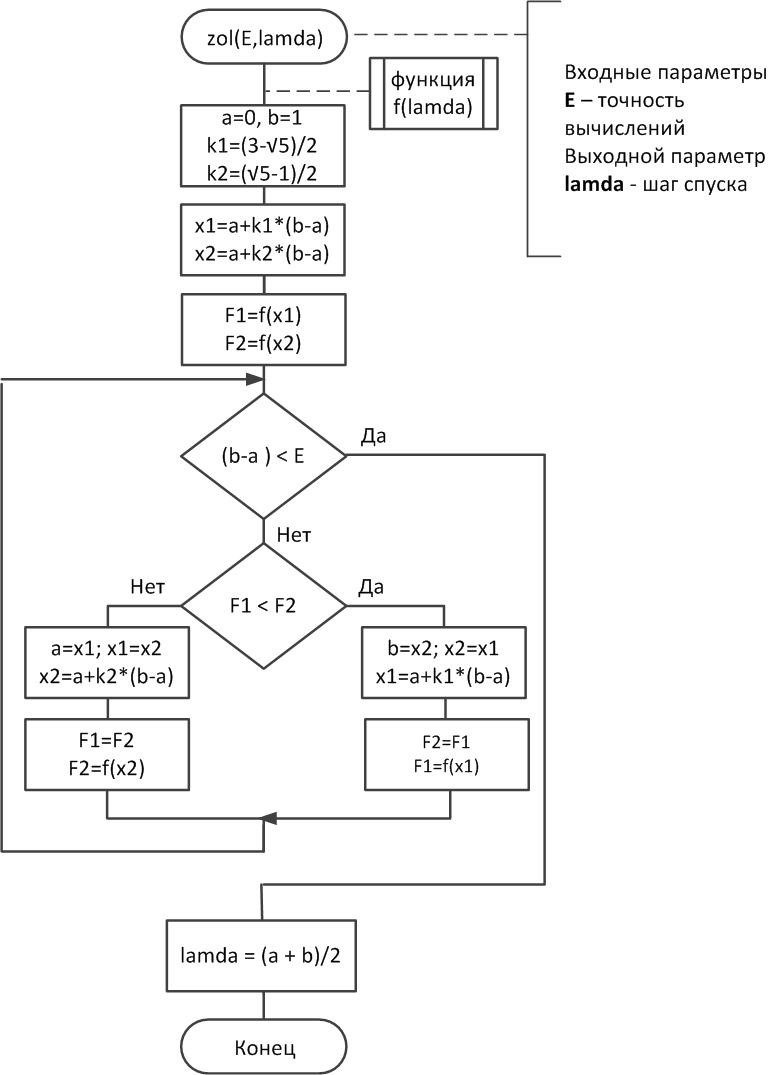
Рис. 2.7-3. Выбор шага в методе НСЧ методом золотого сечения