
- •Введение
- •Основы алгоритмизации
- •Алгоритм, его свойства
- •Базовые алгоритмические структуры
- •Алгоритмы численных методов
- •Алгоритмы методов решения нелинейных уравнений
- •Метод половинного деления
- •Метод итераций
- •Метод Ньютона
- •Метод хорд
- •Алгоритмы методов интерполяции функции
- •Метод Лагранжа
- •Первая интерполяционная формула Ньютона
- •Вторая интерполяционная формула Ньютона
- •Алгоритм аппроксимации функции методом наименьших квадратов
- •Алгоритмы методов численного интегрирования
- •Метод средних прямоугольников
- •Метод трапеций
- •Метод Симпсона
- •Алгоритмы методов решения обыкновенных дифференциальных уравнений
- •Алгоритмы методов одномерной оптимизации
- •Метод дихотомии
- •Метод золотого сечения
- •Метод средней точки
- •Алгоритмы методов многомерной оптимизации
- •Создание схем алгоритмов с использованием графического редактора ms Visio
- •Назначение ms Visio
- •Создание документа, открытие и сохранение файлов
- •Создание простых схем
- •3.4.Настройка внешнего вида блоков схемы алгоритма
- •3.5. Работа с текстом
- •Список литературы
Базовые алгоритмические структуры
Базовыми алгоритмическими структурами принято называть подмножество алгоритмических структур, которые позволяют составить алгоритм решения сколь угодно сложной задачи[2]. Эти структуры могут быть использованы в качестве составляющих разработчиком программы в зависимости от специфики решаемой задачи. К базовым алгоритмическим структурам относятся:
последовательные структуры;
разветвляющиеся структуры;
циклические структуры регулярного типа;
циклические структуры итеративного типа.
Последовательными называются такие алгоритмические структуры, в которых функциональные блоки выполняются в порядке их изображения на схеме алгоритма (рис.1.2-1).

Рис. 1.2-1. Последовательная алгоритмическая структура
Разветвляющимися называются такие алгоритмические структуры, в которых порядок выполнения функциональных блоков определяется значениями логических выражений. Если логическое выражение принимает значение «Истина», то выполняется часть алгоритма, расположенная по ветви «Да», если принимает значение «Ложь», то – часть алгоритма по ветви «Нет».Разветвляющиеся структуры могут быть достаточно сложными, но среди них можно выявить три основных типа разветвлений: стандартное, усеченное и вложенное.
Стандартное разветвлениесодержит функциональные блоки как в ветви «Да», так и в ветви «Нет» (рис.1.2-2).

Рис.1.2-2. Стандартное разветвление
Усеченное разветвление содержит функциональные блоки только в ветви «Да» или только в ветви «Нет» (рис.1.2-3).


Рис. 1.2-3. Типы усеченных разветвлений
Вложенное разветвление содержит одно или несколько дополнительных разветвлений (рис.1.2-4).

Рис. 1.2-4. Вложенное разветвление
В соответствии с основным принципом структурного программирования, все разветвляющиеся структуры, как и все другие алгоритмические структуры, должны иметь один вход и один выход.
Циклическими называются структуры, в которых предусмотрена возможность многократного повторения выполнения участка алгоритма. Этот участок называется телом цикла. Различают циклические структуры двух видов:
-регулярные циклические структуры– это циклические структуры с заранее известным числом повторений;
- итеративной циклической структурой– это циклические структуры с заранее неизвестным числом повторений цикла.
Общий вид алгоритма регулярной циклической структуры приведен нарис.1.2-5.
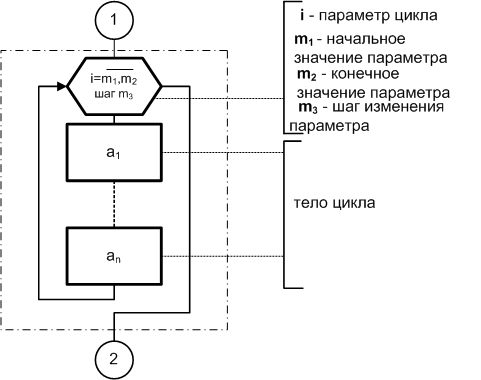
Рис.1.2-5. Регулярная циклическая структура
Здесь в блоке организации цикла используется специальная переменная, которая предназначена для определения условия останова цикла (i). Эта переменная называется параметром цикла. Блоки, следующие за заголовком цикла, составляют тело цикла. Тело цикла выполняется для всех значений параметра цикла i, начинающегося со значения m1и изменяющегося с шагом m3 до значения m2.
Циклическая структура, в которой число повторений цикла заранее неизвестно, а определяется только в процессе выполнения алгоритма, называется итеративной циклической структурой. Важно, чтобы в условие выхода из цикла входила переменная, значение которой изменялось бы в теле цикла, иначе выполнение цикла будет бесконечным.
В зависимости от места расположения условия продолжения цикла (или выхода из цикла) итеративные циклические алгоритмы подразделяются на два вида: с предусловием и с постусловием.
При организации цикла с предусловием (рис.1.2-6) условие выхода из цикла (или выполнения) предшествуют блокам тела цикла, и они выполняются только, если условие L принимает значение «Истина». Выход из цикла происходит при первом невыполнении этого условия. Таким образом, возможен случай, когда тело цикла не будет выполнено ни разу.

Рис. 1.2-6. Итеративная циклическая структура с предусловием
При организации циклов с постусловием, для которых условие выхода из цикла (или повторения тела цикла) проверяется после выполнения цикла (рис.1.2-7). То есть цикл всегда выполняется хотя бы один раз, независимо от значения L, и только после его выполнения принимается решение о продолжении выполнения цикла или выходе из него.

Рис.1.2-7. Итеративная циклическая структура с постусловием
В укрупненных схемах алгоритмов некоторые фрагменты алгоритмов могут быть заменены одним блоком. Простейшим примером такого укрупнения может служить ввод исходных данных, в частности ввод двумерного массива (рис.1.2-8).

(а) (б)
Рис. 1.2-8. Ввод двумерного массива в укрупненном (а) и
детализированном (б) алгоритмах
Из описанных выше базовых алгоритмических структур как из кирпичиков строятся алгоритмы для решения реальных вычислительных задач. В следующем разделе будут приведены вычислительные алгоритмы наиболее распространенных вычислительных методов, которые используются в учебном процессе при изучении вычислительных методов [3] и выполнении курсовых работ.
