
лекции
.pdf
Типовые звенья и их передаточные функции.
Таблица 3.1
21

|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||
|
|
Т1p+1 |
|
|
|
|
|
|
Т2p+1 |
|
|
|
|
1+Т1p+T22p |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
× |
|
= |
|
|
||||||||||||
|
+ 1 |
+ 1 |
1 + + 2 |
|||||||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
2 |
|
|
||||||
1. Безынерционное звено (пропорциональное, усилительное)
( ) = ( ) (3.7)
K – коэффициент передачи (усиления), который является постоянным для линейного звена.
Передаточная функция имеет вид : ( ) = (( )) = ;
Переходная характеристика звена:
( ) = −1[ ( )/ ] = −1[ / ] = × 1( )
Весовая функция пропорционального звена:
( ) = −1[ ( )] = × ( )
Частотные характеристики (АФЧХ, АЧХ, ФЧХ, и ЛАЧХ) звена:
( ) = = +
( ) = √ 2 + 2 =( ) = ( ⁄ ) = 0
( ) = 20lg[ ( )] = 20 lg[ ( )] = 20 lg( )
|
|
X(t) |
|
|
|
|
|
|
W(t)=K*δ(t) |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
K |
|
h(t)=K*1(t) |
|
|
δ(t) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
t |
|
0 |
t |
|
|||
|
|
|
|
|||||||||
|
|
Im |
|
|
|
|
|
A(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[W(jω)] |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
0 |
Re |
|
|
0 |
|
ω |
||
|
|
|
|
|
[W(jω)] |
|
|
|
|
|
|
|
Рисунок 3.2 – Переходная функция, весовая функция, АФЧХ и АЧХ пропорционального звена
Пример физической реализации – жесткий механический рычаг, механический редуктор, потенциометр, усилитель, если уравнения их динамики можно представить уравнениями вида (3.7).
22
ω2=y(t) |
|
= ( 2⁄ |
) |
|
|
1 |
1 |
= 2⁄ 1
( ) = × ( )
ω1=X(t)
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
1 = ( 1 + 2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
2 |
) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U1=x(t) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 + 2 |
1 |
|||||
|
|
|
R |
|
|
U |
|
=y(t) |
|
|
|
|
||||||||
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) = × ( ) |
||||||
Ф( ) = 1( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
07.04.2014 |
|||||
∆(1, ) = ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Апериодическое звено первого порядка |
|
|
|
|
|
|
||||||||||||||
Динамика процесса описывается следующим уравнением: |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
+ ( ) = ( ) (3.8) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где k - передаточный коэффициент или коэффициент усиления, Т - постоянная времени, характеризующая инерционность звена. Применим преобразование Лапласа при нулевых начальных условиях, получим уравнение в операторной форме:
( + 1) × = ( )
Из этого уравнения находится передаточная функция:
TpY p Y p kX p
Y p Tp 1 kX p W p k
Tp 1
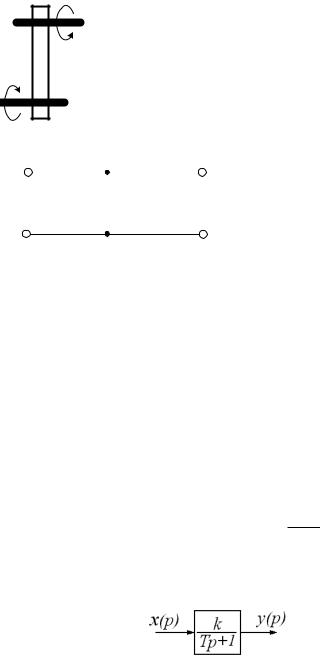
Структурная схема звена при этом будет выглядеть следующим образом:
23
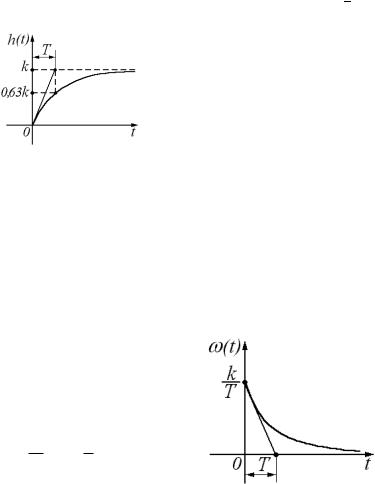
Переходная функция апериодического звена первого порядка:
( ) = −1[ ( ) × 1( )] = −1 [ ( ( + 1))] = ( − − )
= 0; ( ) = 0
= ; ( ) = (1 − 1) ≈ 0,63
= ∞; |
( ) = |
Рисунок 3.3 – переходная характеристика апериодического звена первого порядка
1)→ 0,63
2)в точке ноль строят касательную переходной характеристики, определяют точку пересечения с линией k. Абсцисса этой точки и есть постоянная времени.
Импульсная переходная характеристика, или функция веса,
звена может быть получена путем дифференцирования функции h(t):
|
|
|
t |
|
|
|
t |
|||
|
|
|
|
|
||||||
|
|
|
|
|
k |
|
||||
|
|
|
|
|||||||
t h t k ke |
T |
|
e |
T |
||||||
|
||||||||||
|
|
|
|
|
|
T |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
t 0 |
0 |
k |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
t T T Tek 0,27 Tk t 0
Рисунок 3.4 – весовая функция апериодического звена 1-го порядка
АФХ
Подставляя в передаточную функцию p=j , получим амплитуднофазовую функцию:
W ( j ) |
k |
|
k (1 jT ) |
|
|
k jkT |
|
||||||
|
|
|
|
|
|
|
|
||||||
|
Tj 1 |
|
(1 jT )(1 jT ) |
|
1 T 2 2 |
|
|||||||
Re Im |
k |
j |
|
kT |
|
||||||||
|
|
|
|
|
|
|
|||||||
1 T |
2 2 |
1 T |
2 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
24
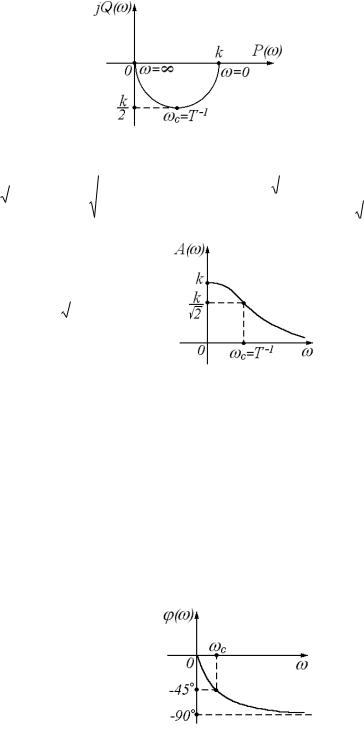
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.5а – АФХ |
|
|
|
|
|
||||
|
АЧХ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
|
|
|
|
|
|
k 2 |
k 2T 2 2 |
k 1 T 2 2 |
|
|
k |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
Re2 Im2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 T 2 2 |
1 T 2 2 |
1 T 2 2 |
|
|
|||||||||||||||
|
|
1 T 2 2 |
||||||||||||||||||
График АЧХ строится по точкам: |
|
|
|
|
|
|
|
|
||||||||||||
0 |
A k |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
A |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
A 0 |
|
|
|
|
|
|
|
|
|
|
||||||||
Здесь с – частота среза.
Гармонические сигналы малой частоты ( < с) пропускаются звеном хорошо – с отношением амплитуд выходной и входной величин, близким к передаточному коэффициенту k. Сигналы большой частоты ( > с) плохо пропускаются звеном: отношение амплитуд существенно больше коэффициента k. Чем больше постоянная времени Т, т.е. чем больше инерционность звена, тем меньше АЧХ вытянута вдоль оси частот, или, тем уже полоса пропускания частот. Т.о. инерционное звено первого порядка по своим частотным свойствам является фильтром низкой частоты.
ФЧХ
ФЧХ инерционного звена первого порядка равна:
|
|
arctg |
Im |
arctg |
kT |
arctg T arctg T |
||||
|
|
Re |
k |
|||||||
|
|
|
|
|
|
|
|
|
||
0 |
0 0 |
|
|
|
|
|
||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
T |
T |
|
|
4 |
|
|
|
|
|
2
Рисунок 3.5в - ФЧХ
25
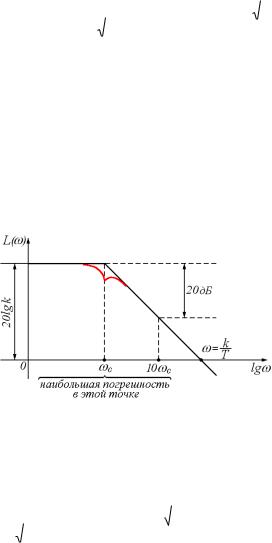
Чем больше частота входного сигнала, тем больше отставание по фазе выходной величины от входной. Максимально возможное отставание равно 900. При частоте с=1/Т сдвиг фаз равен –450.
ЛАЧХ
Рассмотрим теперь ЛАЧХ звена. Точная ЛАЧХ описывается выражением:
|
|
k |
|
|
|
|
|
|
|
|
|
|
|||
L 20lg A 20lg |
|
|
|
|
20lg k 20lg 1 T 2 2 |
||
|
|
|
|
||||
|
|
|
|
||||
|
1 T |
2 2 |
|
|
|
|
|
|
|
|
|
|
|
||
При построении ЛАЧХ апериодического звена прибегают к асимптотическим методам или, другими словами, строят асимптотический график ЛАЧХ.
а) |
1 |
|
L 20lg k |
|
T |
||||
|
|
|
||
б) |
1 |
|
L 20lg k 20lg |
|
T |
|
|||
|
|
|
L 10 20lg k 20lg 102 20lg k 20lg T 20 L L 10 L 20дБ
На втором участке наклон асимптотической ЛАЧХ составляет 20 дБ/дек.
|
|
|
|
|
Рисунок 3.5г - ЛАЧХ |
|
||
a) |
1 |
L 20lg k |
|
|
|
|
||
|
|
|
|
|
||||
c |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
1 |
L 20lg k 20lg 1 20lg k |
|
|
||||
|
|
|
||||||
c |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L 20lg k 20lg |
1 |
|
|
|
|
|||
|
20lg k 20lg |
1 T 2 2 |
20lg k 10lg 2 |
|||||
|
|
|
||||||
|
|
|
1 T 2 2 |
|
|
|
|
|
|
|
|
|
|
|
3дБ |
||
От первых двух точек эта характеристика ЛАЧХ в точке среза будет меньше асимптотической ЛАЧХ на величину 10 lg2 ≈ 3Дб.
26
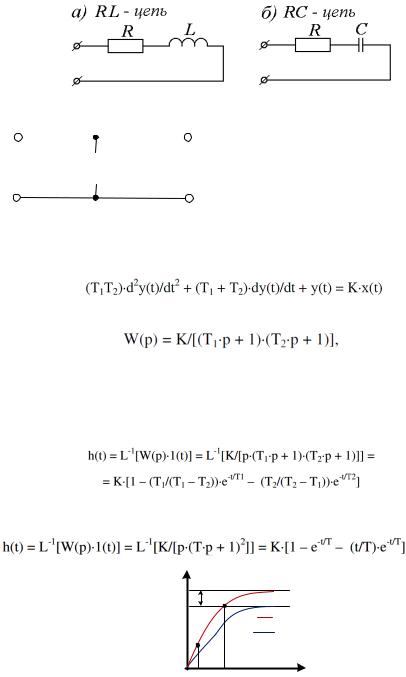
Примеры апериодических звеньев
|
|
R |
|
|
|
|
|
|
|
|
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
= 2 |
+ = 2 + × |
||||||
|
|
|
|
|
|
|
|||||||||
U1=x(t) |
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
С U2=y(t) |
|
( ) |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ ( ) = ( ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
=
3. Апериодическое звено второго порядка
Апериодическое звено второго порядка описывается ДУ II-го порядка:
Передаточная функция апериодического звена II-ого порядка имеет вид:
где K – коэффициент усиления; T1 и T2 – постоянные времени, также характеризующие инерционность системы, т.е. продолжительность переходного процесса в ней. (T1 > 0 и T2 > 0).
Переходная характеристика апериодического звена II-ого порядка имеет вид:
Вчастном случае, когда T1 = T2 = T аналитическое выражение для переходной характеристики имеет несколько иной вид:
h(t) |
|
|
k |
|
|
|
|
T1=Т2 |
|
|
T1<Т2 |
T1 |
Tу |
t |
Рисунок 3.6 – переходная характеристика апериодического звена 2-го порядка
27
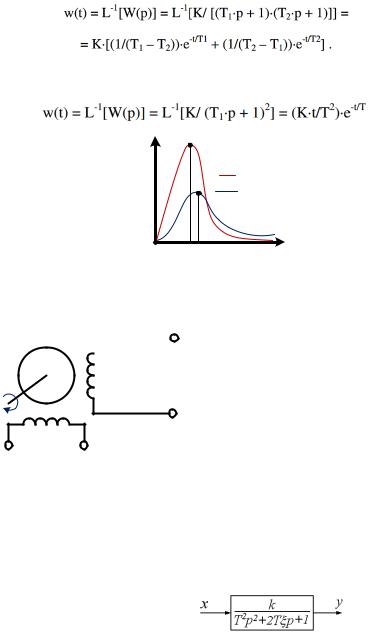
Время регулирования установившегося процесса у ≈ (3 − 5)Т2
Весовая функция апериодического звена II-ого порядка имеет вид:
Вчастном случае, когда T1 = T2 = T аналитическое выражение для весовой функции имеет несколько иной вид:
w(t)
T1=Т2
T1<Т2
0 T1 Tп |
Tу t |
Рисунок 3.7 – весовая функция апериодического звена 2-го порядка
Физическая реализация: центробежный маятник, электродвигатель постоянного тока, двух фазный асинхронный двигатель.
|
|
|
|
|
|
× |
2 |
+ (Т + Т |
) |
|
+ = |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
2 2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||
|
WB |
UB |
|
|
|
1 |
1 |
|
|
|||
ω=y(t) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = 1
2 = /
Uy=x(t)
4. Колебательное звено
Колебательное звено описывается дифференциальным уравнением второго порядка:
T 2 |
d 2 y t |
|
2T |
dy t |
|
y t kx t |
|
dt 2 |
dt |
||||||
|
|
|
|||||
Передаточная функция колебательного звена имеет вид:
W p |
k |
|
|
||
T 2 p2 2T p 1 |
||
|
где k
коэффициент усиления звена; Т постоянная времени колебательного
28
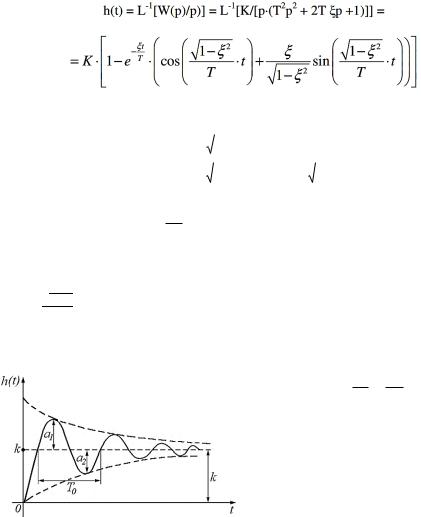
звена; коэффициент демпфирования звена (или коэффициент затухания).
В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:
а) колебательное 0< <1;
б) апериодическое звено II порядка >1;
в) консервативное звено =0;
г) неустойчивое колебательное звено <0.
Переходная характеристика колебательного звена имеет вид:
Или:
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
h t k |
1 |
|
e |
|
|
sin t , где |
|
|
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 2 |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
1 2 |
|
; arctg |
1 2 |
|
; |
||||
|
|
|
|
|
|
|
|
|
||||||
|
T |
|
0 |
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
T0 2 0
Переходная функция имеет достаточно сложный вид, но наиболее характерно то, что имеется экспоненциальное затухание переходного процесса с коэффициентом - ξ/T, а также колебательность с частотой
= √1−2.
Здесь важно отметить, что частота зависит от коэффициента затухания. При ξ → 0 ωк → 1/T; при ξ → 1 ωк → 0.
Амплитуды первых двух колебаний определяют величину -
1 ln a1
T0 a0 .
Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, тем меньше Т, тем быстрее устанавливаются переходные процессы.
29
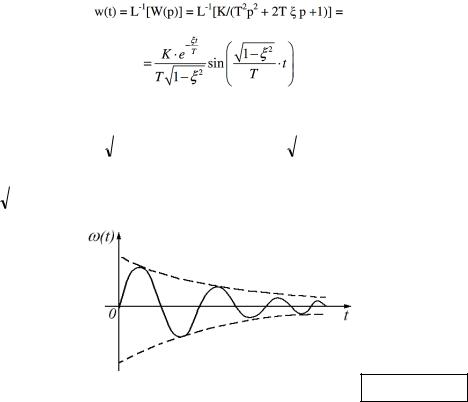
Весовая функция колебательного звена имеет вид:
Или: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
|
|
|
|||||
t h t k |
|
|
|
|
et sin |
t |
e |
|
|
cos |
t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ket |
|
sin |
t |
cos t |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 2 |
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
14.04.2014
Структурные схемы САУ
Для оценки точности, устойчивости и качества управления замкнутых систем необходимо знать их уравнения статики и динамики. Уравнение динамики замкнутой системы можно получить на основе совокупности уравнений отдельных элементов, образующих систему, путем последовательного исключения промежуточных переменных. Наиболее удобным для решения этой задачи объединения математических моделей элементов является
метод структурных преобразований, согласно которому по структуре схемы с помощью нескольких простых правил находят ее общую (эквивалентную) передаточную функцию, а затем – соответствующее уравнение динамики.
Структурные схемы САУ - это графическое изображение САУ, где динамика процессов представлена в операторной форме в виде передаточных функций.
30
