
лекции
.pdf
Адаптивные системы
Если параметры объекта или возмущений известны неточно или могут изменяться со временем (в нестационарных системах),
применяют адаптивные или самонастраивающиеся регуляторы, в
которых закон управления меняется при изменении условий. В простейшем случае (когда есть несколько заранее известных режимов работы) происходит простое переключение между несколькими законами управления. Часто в адаптивных системах регулятор оценивает параметры объекта в реальном времени и соответственно изменяет закон управления по заданному правилу.
Самонастраивающаяся система, которая пытается настроить регулятор так, чтобы «найти» максимум или минимум какого-то критерия качества, называется экстремальной (от слова экстремум, обозначающего максимум или минимум).
03.03.2014
Математическое описание линейных САУ.
Описание звеньев во временной (t) и частотных ( ) областях, а также комплексной переменной (s).
a) |
б) |
||||||||||||||
|
x(t) |
|
|
|
y(t) |
|
|
x(ω) |
|
|
|
y(ω) |
|||
|
|
W(p) |
|
|
|
W(jω) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
в) x(s) |
|
|
y(s) |
|
||||||||
|
|
|
|
W(s) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
а) во временной области; б) в частотной области; в) в области комплексной переменной
Рисунок 12 – динамическое звено
X(s) – изображение по Лапласу.
= +≡ ≡
p – оператор дифференцирования= – частотная область
В общем случае система с одной входной переменной x(t) и одной выходной y(t) во временной области может быть записана в виде
дифференциальных уравнений. |
|
|
|
|
|
|
||||||||
|
|
|
−1 |
|
|
|
|
|||||||
0 ( |
|
) + 1 ( |
|
) + + −1 |
|
|
+ |
|||||||
|
−1 |
|
||||||||||||
= ( |
|
) + ( |
−1 |
) + |
|
|
+ |
|||||||
|
−1 |
|
||||||||||||
0 |
1 |
−1 |
|
|
||||||||||
Для физически реализуемых систем . |
|
|
|
|
|
|||||||||
Если ввести оператор |
дифференцирования |
|
= ⁄ , то можно |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записать в виде алгебраического уравнения |
во временной области. |
|||||||||||||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
||
( 0 + 1 −1 + + −1 + ) ( )
= ( 0 + 1 −1 + + −1 + ) ( ) (2.2)
Для s-области входные и выходные значения переменных звеньев записываются в виде преобразования Лапласа – L. Основным описанием звена в этом случае является передаточная функция - отношение преобразования Лапласа (изображение) выходной величины к изображению входной величины при нулевых начальных условиях : ( ) = ( )/( ),
где s – комплексная переменная = + .
Для обозначения сигналов и переменных в комплексной форме будем использовать прописные буквы.
Связь между оригиналом сигнала x(t) и его изображением X(s) в преобразовании Лапласа для входной переменной имеет вид:
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
( ) = [( )] = ∫ ( ) − |
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
( |
) |
−1{ |
( ) |
} |
1 |
( ) |
|
|
|
|
|
= |
|
= ( ⁄2) ∫ |
|
|||
|
|
|
|
|
|
− |
|
|
|
Таблица преобразований Лапласа |
|
|
|
||||||
х(t) (t > 0) |
|
|
|
|
Х(s) = L[х(t)] |
|
|
|
|
1(t) |
|
|
|
|
|
1/s |
|
|
|
δ(t) |
|
|
|
|
|
1 |
|
|
|
t |
|
|
|
|
|
1/s2 |
|
|
|
tn |
|
|
|
|
|
n!/sn+1 |
|
|
|
eat |
|
|
|
|
|
1/(s – a) |
|
|
|
e-at |
|
|
|
|
|
1/(s + a) |
|
|
|
t·eat |
|
|
|
|
|
1/(s – a)2 |
|
|
|
tn·eat |
|
|
|
|
|
n!/(s – a)n+1 |
|
|
|
sin(ωt) |
|
|
|
|
|
ω/(s2 + ω2) |
|
|
|
cos(ωt) |
|
|
|
|
|
s/(s2 + ω2) |
|
|
|
sin(ωt + φ) |
|
|
[sin(φ) ·s + cos(φ) ·ω]/(s2 + ω2) |
|
|
||||
cos(ωt + φ) |
|
|
[cos(φ) ·s – sin(φ) ·ω]/(s2 + ω2) |
|
|
||||
eat·sin(ωt) |
|
|
|
ω/[(s – a)2 + ω2] |
|
|
|
||
eat·cos(ωt) |
|
|
|
(s – a)/[(s – a)2 + ω2] |
|
|
|
||
eat·sin(ωt + φ) |
[sin(φ) ·(s – a) + cos(φ) ·ω]/[(s – a)2 + ω2] |
||||||||
eat·cos(ωt + φ) |
[cos(φ) ·(s – a) – sin(φ) ·ω]/[(s – a)2 + ω2] |
||||||||
Таким образом в s-области запись уравнения в операторной форме изображений по Лапласу входной X(s) и выходной Y(s) переменных по структуре совпадает с (2.2), но при использовании комплексной переменной = + :
( 0 + 1 −1 + + −1 + ) ( )
= ( 0 + 1 −1 + + −1 + ) ( )
Или в виде передаточной функции:
12
( )( ) = ( ) ( . )
Для частотной области: ( ) = ( )/ ( )
|
∞ |
|
|
( ) = {( )} = ∫ |
|
( ) − |
|
−∞ |
|
||
( ) = −1{( )} = (1⁄ |
|
∞ |
|
|
)∫ |
( ) |
|
2 |
−∞ |
|
|
Так частотную передаточную функцию можно получить из (2.4) путем подстановки = , при = 0
Изображение Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
( ) + ( ) −1 |
+ + |
|
|
( ) + |
|
||
( ) = |
|
= |
0 |
|
1 |
−1 |
|
|
= |
||
( ) |
|
|
( ) + ( ) −1 |
+ + |
−1 |
( ) + |
|
||||
|
|
|
|
||||||||
|
|
|
0 |
1 |
|
|
|
|
|||
= ( ) + ( ) (2.5)
Любое динамическое звено в автоматике можно записать в виде типового воздействия.
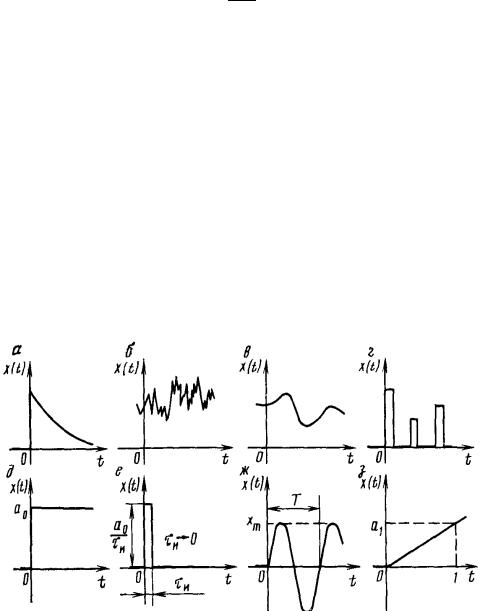
а) регулярное воздействие, б) случайное, в) непрерывное, г) дискретное, д) ступенчатое, е) импульсное, ж) гармоническое, з) линейно возрастающее.
13

1.Ступенчатое воздействие - воздействие, которое мгновенно возрастает от 0 до некоторого значения и далее остается постоянным.
Ступенчатому воздействию соответствуют функции:
0, при < 0( ) = { 0, при ≥ 0
При 0 = 1 (единичное воздействие) – функция Хевисайда.
2.Импульсное воздействие – одиночный импульс прямоугольной формы, имеющий достаточно большую высоту и весьма малую продолжительность.
Единичное импульсное воздействие, которое описывается дельтафункцией (функцией Дирака):
0, при ≠ 0( ) = {∞, при = 0
Причем, ∫−∞∞ ( ) = 1
Дельта-функцию можно рассматривать как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь.
Дельта-функция определяется как производная единичного скачка.
1( )( ) =
3. Гармоническое воздействие – сигнал синусоидальной формы.
( ) = (−∞ < 1 < ∞)
A – амплитуда сигнала
= 2 / – круговая частота, рад/с
Т– период сигнала, с.
4.Линейное воздействие
( ) = 1( ) 1 (0 ≤ < ∞)
а1 характеризует скорость нарастания воздействия x(t).
Временные характеристики. |
17.03.2014 |
|
|
|
Переходные характеристики H(t) (кривые разгона).
Весовые (импульсные переходные) функции (t).
Частотные характеристики.
АФХ (АФЧХ) или частотная передаточная функция.
АЧХ
Фазо-частотная характеристика ФЧХ (ЛФЧХ)
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ либо ЛАХ)
Логарифмическая фазо-частотная характеристика (ЛФЧХ/ЛФХ).
14
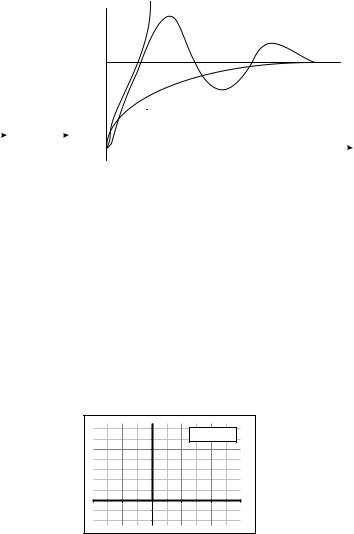
Переходные характеристики.
Переходная, или временная характеристика (функция) звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция) –
это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным. Сказанное иллюстрируется на рис.2.6,а и б. На рис. 2.6,б показаны три различных вида переходных характеристик, соответствующих различным типам звеньев.
y 
|
|
|
|
|
|
x 1(t) |
||
|
|
|
y |
|
|
|
||
x |
|
|
|
|
t |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
0 |
|
|
|||
|
|
б) |
||||||
|
|
|
|
|
||||
Рис. 2.6. Переходные характеристики.
Таким образом, h(t) – это выражение для y(t) при x(t) = 1(t).
Наряду с переходной характеристикой применяется импульсная переходная (временная) характеристика или функция, называемая еще весовой функцией (функцией веса) – отклик на дельта-функцию (функцию Дирака). Эта характеристика представляет собой реакцию звена на единичный импульс.
Единичный импульс (единичная импульсная функция, или
дельта-функция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности. На рисунке б) он условно показан в виде утолщения на оси ординат.
x(t) = (t)
1
-2 |
-1 |
0 |
1 |
2 |
3 |
Рисунок б
15
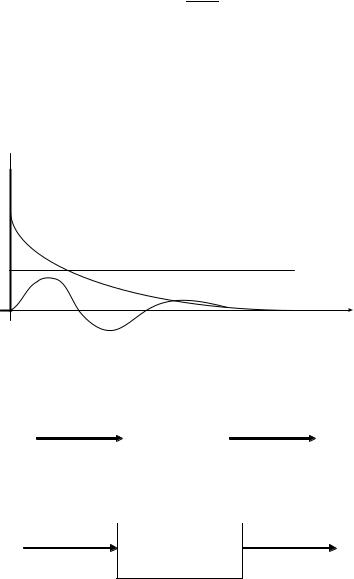
Импульсная переходная функция w(t) равна производной от переходной функции h(t).
( )( ) =
И наоборот, переходная функция равна интегралу от импульсной переходной функции:
( ) = ∫ ( )
0
На рис. 2.7 изображены типичные формы самих импульсных переходных характеристик.
y 
x (t)
t
0
Рис. 2.7. Импульсная переходная (весовая) характеристика.
Функции 1(t) и δ(t) можно использовать для экспериментального определения передаточной функции элемента системы управления:
y(t) = δ(t) |
|
|
x(t) = w(t) |
|
|
|
W(s) |
|
|
|
|
|
|
|
|
|
|
Первый подход: подадим на вход *(t). |
Пусть *(t) ≈ |
(t) (т.к. |
(t) |
||
физически не реализуема), измерим w*(t) ≈ w(t). Теперь можно вычислить L[w*(t)] = W*(s) ≈ W(s), т.е. ( ) = −1[( )] (2.6)
y(t) = 1(t) |
|
x(t) = h(t) |
|
W(s)
Второй подход: На вход подаем 1(t). Измеряем h(t) и вычисляем передаточную функцию. W(s) = L[d/dt(h(t)].
В случае, когда x(t) = 1(t), учитывая, что L(1(t))=1/s, получаем выражение для изображения переходной характеристики:
16
( )
Соответственно переходная характеристика звена:
( ) = −1 [ ( )]
Выражение 2.6 можно трактовать как определение передаточной функции – изображение Лапласа весовой функции.
Зная переходную функцию можно определить реакцию звена и другим способом – с помощью интеграла Дюамеля (свертка).
t |
|
y(t) h(t)x(0) h(t )x' ( )d , |
(2.7) |
0
где х(0) – значение х(t) при t = 0;
t |
|
|
y(t) h(0)x(t) w(t )x( )d |
(2.8) |
|
0 |
||
|
Эти формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки.
Частотные характеристики.
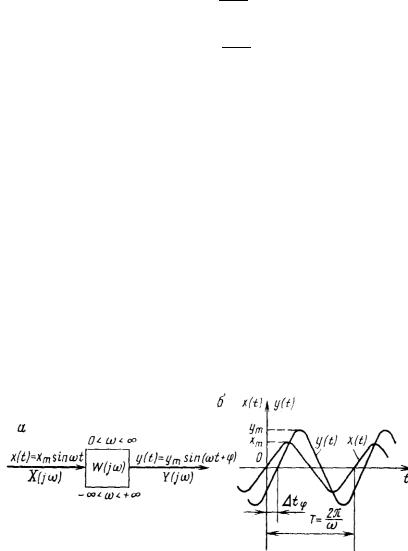
Частотная характеристика – отношение реакции (отклика) звена y(t) к синусоидальному входному воздействию ( ) = . Реакция в этом случае так же будет представлять гармонический сигнал, но с другой амплитудой и фазовым сдвигом ( ) = sin( + ).
Рисунок 2.5 - реакция звена на гармоническое воздействие
Частотная характеристика w(j ) может быть определена по (2.5) На рисунке 2.8 в АФХ P(j ) – четная, Q(j ) – нечетная функция. АФЧХ W(j ) в показательной форме:
( ) = ( ) ( )
A(ω) – модуль АФХ, а φ( ) – угол сдвига по фазе. Алгебраическая форма:
( ) = ( ) + ( )
Тригонометрическая форма:
17
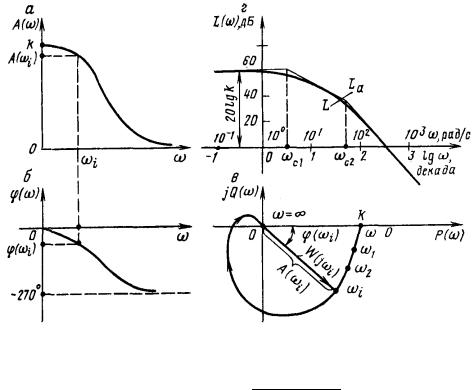
( ) = А( ) ( ) + ( ) sin ( )
Рисунок 2.8
Связь между различными частотными функциями:
( ) = |( )| = √2( ) + 2( )
|
|
|
( ) = arg ( ) = |
( ) |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
( ) |
|
|
|
|||||||
На рисунке 2.8 (г) показана ЛАЧХ L( и соответствующая ей |
|||||||||||||
приближенная характеристика L0( ). |
|
|
|
|
|
|
|
||||||
Обычно в расчетах используют ЛАЧХ. |
|
|
|
|
|
|
|
||||||
|
|
|
|
( ) = 20 log ( ) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
0,01 |
0,01 |
|
0,316 |
0,89 |
|
1 |
|
1,12 |
3,16 |
10 |
100 |
|
L,дБ |
-60 |
-40 |
|
-10 |
-1 |
|
0 |
|
1 |
10 |
20 |
40 |
|
За единицу длины по оси частот логарифмических характеристик принимают декаду.
Декада – интервал частот, заключенный между произвольным значением частоты i и его десятикратным значением 10 i . Рассмотренные выше временные, передаточные и частотные характеристики однозначно связаны меду собой прямым и обратным преобразованиями Лапласа и Фурье. Это отражено в таблице.
18
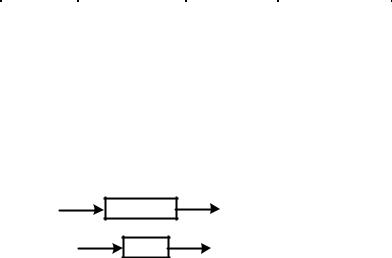
Таблица - Взаимные соответствия динамических характеристик.
Характер-ки |
h(t) |
w(t) |
W(p) |
|
W(j ) |
|
|
|
|
||||
|
|
|
|
|
|
|
Переходная |
|
t |
|
|
|
|
1 |
w( )d |
L-1{W(s)/s} |
F-1{W(j )/ j } |
|
||
h(t)= |
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Импульсная |
dh(t)/dt |
1 |
L-1{W(s)} |
|
F-1{W(j )} |
|
w(t)= |
|
|
||||
|
|
|
|
|
|
|
Передаточная |
sL{h(t)} |
L{w(t)} |
1 |
|
W(j ) s=j |
|
W(s)= |
|
|
||||
|
|
|
|
|
|
|
Частотная |
j F{h(t)} |
F{w(t)} |
W(s) s=j |
|
|
|
W(j )= |
1 |
|
||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
31.03.2014 |
|
|
|
|
|
|
|
|
Типовые динамические звенья САУ и их характеристики.
a)
x(t) Элемент y(t)
б) x(t) W(s) y(t)
Рисунок 3.1 – а) элемент и б) динамическое звено САУ
В изображениях Лапласа (см. формулу 2.4) при обозначении s=p:
|
( ) |
+ −1 |
+ + |
|
|
+ |
|
|||
= |
|
= |
0 |
1 |
−1 |
|
|
(3.1) |
||
( ) |
|
+ −1 |
+ + |
−1 |
+ |
|
||||
|
|
|
0 |
1 |
|
|
|
|
||
Передаточную функцию системы можно представить в виде произведения простых множителей и дробей.
; ; 1⁄ ; ± 1; 1⁄( ± 1)
2 2 ± 2 + 1; 1/( 2 2 ± 2 + 1) (3.2)
K – коэффициент передачи или коэффициент усиления,
Т – инерционность или постоянная времени инерционного звена,– коэффициент затухания (демпфирования)
Сомножители представляющие звенья: пропорциональные K, дифференцирующие - ± 1, апериодические первого порядка,
1⁄( ± 1), форсирующее первого порядка ± 1, интегрирующее -
1⁄ , форсирующее второго порядка - 2 2 ± 2 + 1, апериодическое
19
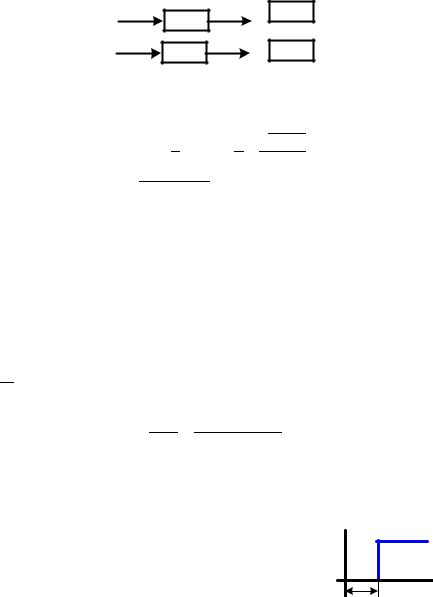
второго порядка - 1/( 2 2 |
± 2 + 1), |
|
при |
|
1 ≤ , |
колебательное - |
|||||||||||||||||
1/( 2 2 ± 2 + 1) при 0 < < 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x(t) |
W(p) |
y(t) |
1/Tp |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W(s) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
Tp |
|
||
Для каждого из звеньев могут быть найдены корни для уравнений, |
|||||||||||||||||||||||
записанных в числителе или знаменателе, представляющих их |
|||||||||||||||||||||||
формулу. Корни числителя – нули 0, |
для знаменателя - полюса . |
||||||||||||||||||||||
Для отдельных звеньев корни будут иметь вид: |
|
||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
= − |
1 |
; 0 |
|
= − |
|
|
√ 2 |
− 1 |
|
|||||
|
|
|
|
|
= 0; 0 |
|
|
|
|
± |
|
, = 1 |
|||||||||||
|
|
|
|
|
|
0 = |
− ± cos ; 0 < < 1 |
|
|
(3.3) |
|
||||||||||||
- полюса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0- нули |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Динамическое звено – звено, описываемое дифференциальными |
|||||||||||||||||||||||
уравнениями не выше второго порядка. |
|
|
|
|
|
||||||||||||||||||
Таким образом, типовые звенья описываются уравнениями: |
|||||||||||||||||||||||
|
|
|
′′( ) + |
′( ) + |
( ) = ′( ) + ( ) |
(3.4) |
|||||||||||||||||
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
1 |
|
Принято так же приводить уравнение звена к стандартному виду в |
|||||||||||||||||||||||
операторной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
( |
2 2 + + 1) = ( |
|
+ 1) |
|
|
(3.5) |
|
||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
0 |
; 1 |
= |
1 |
; = |
|
0 |
|
– постоянные времени. |
|
|||||||||||||
2 = |
⁄ 2 |
|
⁄ 2 |
|
|
⁄ |
|
|
|||||||||||||||
= 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или в виде передаточной характеристики: |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
( ) = |
( ) |
|
|
|
( + 1) |
|
|
|
|
||||||||
|
|
|
|
|
|
( ) |
= 2 2 + + 1 (3.6) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
Если |
а2 |
и |
|
|
b1≠0, |
то |
|
|
такие |
звенья |
называют |
позиционными |
|||||||||||
(статическими). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если |
а2 |
и b1=0, то такие звенья называют астатические (в |
|||||||||||||||||||||
переходном процессе характеристика выходит на ноль, т.е. |
|||||||||||||||||||||||
статическая ошибка равна 0). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Звенья |
делятся |
|
на |
|
|
|
инерционные |
|
и |
|
|||||||||||||
безынерционные. Безынерционное – усилительное |
|
||||||||||||||||||||||
(пропорциональное) звено К., инерционные – звено, |
|
||||||||||||||||||||||
где есть знаменатель + 1 (замедление).Звенья с |
|
||||||||||||||||||||||
чистым запаздыванием. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
