20.Моделирование двухуровневой организационной системы (детерминированный вариант).

Рассмотрим организационную систему, состоящую из Центра и «л» производственных элементов (ПЭ).

Каждый производственный элемент характеризуется показателем эффективности r_i, и функцией затрат z_i. Показатель r_i характеризует эффективность работы i — го производствен­ного элемента. Он определяется условием автоматизации, механизации, применением ресур­сосберегающих технологий, организации производства и т.д. Примем далее, что затраты i - го производственного элемента описываются следующей моделью:

z_i=x²_i/2r_i, где х, - объем работ, выполненный i - ым производственным элементом.

Перед Центром стоит задача распределения между производственными элементами работ в объемеR таким образом, чтобы затраты всей системы были минимальны. То есть центр решает следующую оптимизационную задачу:

Если Центру известны реальные значения показателей эффективности r_i(случай определенности), то решением задачи является закон пропорционального распределения:

21.Методы снятия неопределенности (принципы гарантированного результата).

В задачах существуют параметры. ЛПР должно обладать информацией о значениях этих параметров.

a_ij – значения этих параметров,

c_j – коэффициент целевой функции.

С точки зрения формализованного описания можем сказать, что ЛПР имеет представление об области допустимых значений параметров (а А).

Чем больше ОДЗ, тем больше неопределенность.

Решаем задачу «снятия неопределенности».

Приемы:

Принцип гарантированного результата. Этот принцип предполагает, что лицо, принимающее решение, исходит из наихудшей гипотезы о значениях параметров.

Для определенности допустим, что рассматривается некоторый параметр аi, который имеет положительный смысл (цена на продукцию, спрос на нашу продукцию)

-ОДЗ

22.Методы снятия неопределенности (метод регрессионного прогнозирования).

В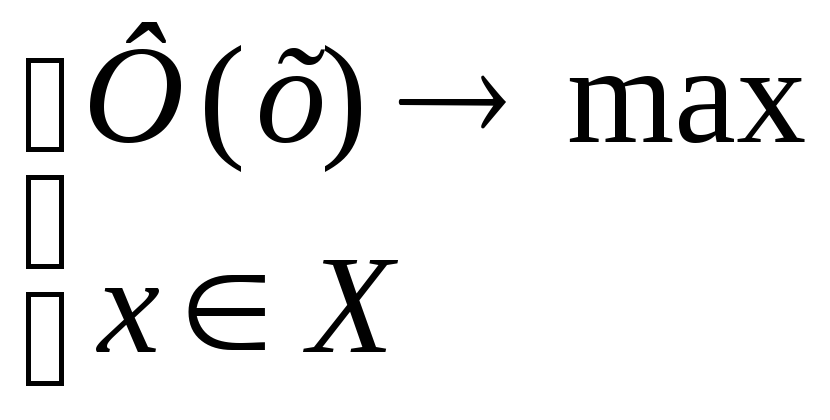задачах существуют параметры. ЛПР должно обладать информацией о значениях этих параметров.

a_ij – значения этих параметров,

c_j – коэффициент целевой функции.

С точки зрения формализованного описания можем сказать, что ЛПР имеет представление об области допус. значений параметров (аА).

Чем больше ОДЗ, тем больше неопределенность.

Р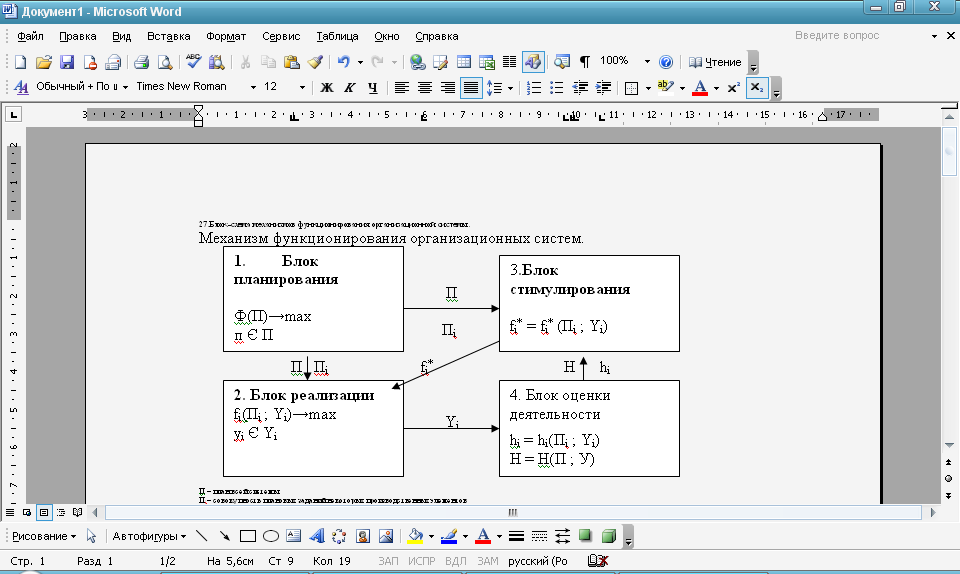ешаем задачу «снятия неопределенности».

Метод статистического моделирования. Идея метода заключается в следующем: ЛПР не имеет достоверной информации о значениях параметров на будущие периоды. Однако, он располагает ретро информацией о значениях этих параметров.

Бывают ситуации, когда изменение параметров характеризуется некоторой тенденцией. Если такое имеет место, то возникает идея построить некоторую функцию, которая описывает эти закономерности а = а(t) Возьмем некоторую линейную матрицу: а = α + βt

Есть некоторая статистика. Имея некоторые прочие данные, используя МНК рассчитываются параметры α и β. Тогда модельное значение параметров а^м = α + βt.

Рассчитывается погрешность:

Эти методы применимы только в случаях, когда медленно развиваются процессы.

23-24.Методы снятия неопределенности (метод формирования данных).

В задачах существуют параметры. ЛПР должно обладать информацией о значениях этих параметров.

a_ij – значения этих параметров,

c_j – коэффициент целевой функции.

С точки зрения формализованного описания можем сказать, что ЛПР имеет представление об области допустимых значений параметров (а А).

Чем больше ОДЗ, тем больше неопределенность.

Решаем задачу «снятия неопределенности».

Метод формирования данных.

ЛПР просит сообщить элемента значение параметра а.

S – та оценка, которую элемент сообщит наверх в качестве значения параметра.

Поскольку ЛПР имеет представление об ОДЗ, то сообщаемая оценка может колебаться в диапазоне:

Есть серьезные недостатки в этом методе: ЛПР должен понимать, что у элементов есть свое представление что сообщать и как сообщать. Элементы могут сознательно искажать информацию.