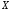- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
10. Дискретные св. Закон распределения дискретной св.
Определение.
Случайная величина
 ,
заданная на вероятностном пространстве
,
заданная на вероятностном пространстве ,
называетсядискретной,
если множество ее возможных значений
,
называетсядискретной,
если множество ее возможных значений конечно
или счетно:
конечно
или счетно:
 или
или
 .
.
Для
полной вероятностной характеристики
дискретной случайной величины
 достаточно указать все ее возможное
значения
достаточно указать все ее возможное
значения и вероятности
и вероятности ,
с которыми эти значения принимаются,
,
с которыми эти значения принимаются, .
При этом, поскольку события
.
При этом, поскольку события ,
, ,
образуют полную группу событий, то
,
образуют полную группу событий, то
 (условие
нормировки).
(условие
нормировки).
Подобную информацию о дискретной случайной величине записывают в виде таблицы:
|
|
|
|
|
|
|
(2.1) |
|
|
|
|
|
|
|
которую
называют законом
распределения
дискретной случайной величины
 илирядом
распределения.
илирядом
распределения.
Функция
распределения дискретной случайной
величины определяется по закону
распределения (2.1) с помощью формулы:
 .
(2.2)
.
(2.2)
Подробнее в случае конечного числа значений дискретной случайной величины формула (2.2) выглядит следующим образом:

График
функции распределения дискретной
случайной величины является
кусочно-постоянным со скачками в точках
 равными
равными ,
,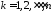 .
Это означает, что закон распределения
(2.1) по функции распределения (2.2) всегда
можно однозначно восстановить.
.
Это означает, что закон распределения
(2.1) по функции распределения (2.2) всегда
можно однозначно восстановить.

Вероятность
попадания дискретной случайной величины
 в любое борелевское множество на числовой
прямой
в любое борелевское множество на числовой
прямой определяется по формуле:
определяется по формуле: .
.
Отметим,
что через функцию распределения
вероятность
 в явном виде может и не выражаться.
в явном виде может и не выражаться.
11. Важнейшие дискретные св.
Вырожденная случайная величина.
Любую
константу С
можно рассматривать как случайную
величину, принимающую одно значение:
 для любого
для любого .
.
Закон распределения вырожденной случайной величины имеет вид:
|
|
С |
|
|
1 |
Выражение для функции распределения вырожденной случайной величины и ее график также имеют вырожденный вид:

С
x
F(x)
1
0





2. Индикаторная случайная величина.
С любым случайным событием А можно связать случайную величину вида:
 .
.
Случайная
величина
 называетсяиндикатором
случайного события А
или индикаторной
случайной величиной.
Она принимает только два значения
называетсяиндикатором
случайного события А
или индикаторной
случайной величиной.
Она принимает только два значения
 и
и ,
при этом
,
при этом
 ,
,
 .
.
Закон распределения индикаторной случайной величины имеет вид:
|
|
0 |
1 |
|
|
q |
p |
Аналитическое выражение и график функции распределения имеют вид:
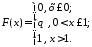

3. Биномиальная случайная величина.
Биномиальной
называется дискретная случайная величина
 ,
представляющая собойчисло
успехов
в n
независимых испытаниях, проводимых по
схеме Бернулли, с вероятностью успеха
в одном испытании равной р.
,
представляющая собойчисло
успехов
в n
независимых испытаниях, проводимых по
схеме Бернулли, с вероятностью успеха
в одном испытании равной р.
Множество возможных значений биномиальной случайной величины:
 .
.
Вероятности, с которыми значения принимаются, определяются по формуле Бернулли:
 .
.
Закон распределения имеет вид:
|
|
0 |
1 |
|
n |
|
|
|
|
|
|
и называется биномиальным законом распределения.
Условие
нормировки при этом следует из формулы
Бернулли или непосредственно из бинома
Ньютона:
 .
.
(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).
Сокращенное
обозначение для биномиальной случайной
величины:
 .
.
4. Геометрическая случайная величина.
Геометрической
называется дискретная случайная величина
 ,
представляющая собойчисло
испытаний,
проводимых по схеме Бернулли, до появления
первого успеха с вероятностью успеха
в одном испытании равной р.
,
представляющая собойчисло
испытаний,
проводимых по схеме Бернулли, до появления
первого успеха с вероятностью успеха
в одном испытании равной р.
Геометрическая случайная величина имеет счетное множество возможных значений:
 .
.
Вероятности значений определяются по формуле:
 .
.
Закон распределения имеет вид:
|
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
и называется геометрическим законом распределения.
Условие
нормировки при этом следует из формулы
для суммы бесконечно убывающей
геометрической прогрессии:
 .
.
(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).
Сокращенное
обозначение для геометрической случайной
величины:
 .
.
5. Пуассоновская случайная величина.
Пуассоновской
называется целочисленная случайная
величина, множество возможных значений
которой
 ,
,
а
вероятности, с которыми значения
принимаются, задаются формулой: .
.
Число
 называется параметром пуассоновской
случайной величины.
называется параметром пуассоновской
случайной величины.
Закон распределения имеет вид:
|
|
0 |
1 |
|
n |
|
|
|
|
|
|
|
|
и называется пуассоновским законом распределения.
Условие нормировки при этом следует из разложения экспоненты в ряд Тейлора:
 .
.
(Записать аналитическое выражение для функции распределения и построить ее график самостоятельно).
Сокращенное
обозначение для пуассоновской случайной
величины: .
.