37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.

Пусть - последовательность независимых одинаково распределенных случайных величин с конечными математическим ожиданиеми дисперсией,- сумма первыхслучайных величин.

В соответствии с законом больших чисел для независимых одинаково распределенных случайных величин (Теорема 3)

или, после приведения к общему знаменателю, .

Возникает вопрос: если при делении на мы получили в пределе 0 (в смысле некоторой, все равно какой, сходимости), то не слишком ли на «много» мы поделили? Нельзя ли поделить на что-нибудь, растущее кмедленнее, чем, чтобы получить в пределе не 0 (и не, естественно)? Оказывается, что уже последовательность случайных величинсходится не к 0, а к случайной величине,причем имеющей нормальный закон распределения!!!

Теоремы, которые устанавливают нормальность предельного (в смысле слабой сходимости) закона распределения суммы случайных величин называются центральными предельными теоремами (ЦПТ).

Теорема 1 (ЦПТ для независимых одинаково распределенных случайных величин).

Пусть - последовательность независимых одинаково распределенных случайных величин, имеющих конечные математическое ожидание и дисперсию ,- сумма первыхслучайных величин.

Тогда при последовательность случайных величинслабо сходится к стандартному нормальному закону распределения:

или, что эквивалентно, последовательность функций распределения сходится к функции распределениястандартного нормального закона распределения (функции Лапласа) равномерно по всем:.

Замечание. Учитывая, что 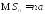, аи согласно определениям функции распределения и функции Лапласа, утверждение Теоремы 1 можно переписать в следующем виде.

Последовательность центрированных и нормированных сумм независимых случайных величин 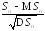слабо сходится прик стандартному нормальному закону распределения:

или, что эквивалентно, равномерно по всем

▲ Обозначим 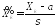независимые случайные величины, имеющиеи,(стандартизованные случайные величины) и пусть. Так как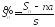, то требуется доказать, что.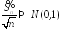

Вычислим характеристическую функцию случайной величины .

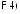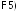Применяя свойства и, имеем:.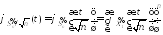

В соответствии со свойством 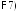характеристическую функциюслучайной величиныможно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты:,:.

Подставляя полученное разложение, взятое в точке 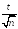, в выражение для, получаем:

.

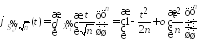Устремляя и воспользовавшись вторым замечательным пределом, имеем:.

В пределе мы получили характеристическую функцию стандартного нормального закона распределения . По теореме непрерывности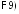можно сделать вывод о слабой сходимости припоследовательности функций распределенияк функции распределения стандартного нормального закона распределения:. При этом, поскольку предельная функция распределенияявляется непрерывной на всей числовой прямой, то сходимость функций распределения является равномерной по■.

Следствие (Интегральная предельная теорема Муавра-Лапласа).

Обозначим - число успехов внезависимых испытаниях по схеме Бернулли с вероятностью успеха в каждом испытании равной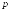,(то есть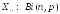). Тогда при

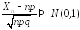
или, что эквивалентно, при равномерно по всем:.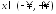

В частности, при больших и любых неотрицательных целыхи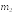

.

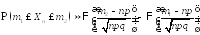▲ Доказательство первого утверждения непосредственно следует из Теоремы 1, поскольку случайная величина является суммой независимых одинаково распределенных случайных величин: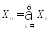, где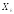- число успехов в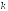-ом испытании,,,(см. доказательство теоремы Бернулли).

Второе утверждение следует из первого и свойств функции распределения:

■.

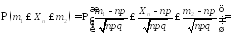
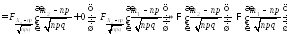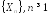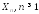Если - последовательность независимых, разно-распределенных случайных величин, то для справедливости ЦПТ уже необходимо накладывать на случайные величинынекоторые ограничения. Наиболее общим результатом в этом направлении является следующая теорема.