16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.

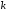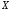Определение. Начальным моментом -го порядка случайной величиныназывается математическое ожидание-ой степени этой случайной величины: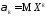, (2.9)

если математическое ожидание существует.

Как правило, используют начальные моменты целого положительного порядка. В частности, приимеем, а при.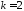

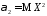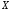Определение. Центральным моментом -го порядка случайной величиныназывается математическое ожидание-ой степени отклонения этой случайной величины от ее математического ожидания: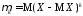, (2.10)

если математическое ожидание существует.

Случайная величина 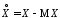называется центрированной случайной величиной. Очевидно,. Таким образом, центральный момент – это начальный момент для центрированной случайной величины:.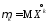

Аналогично начальным моментам, используются центральные моменты , как правило, целого положительного порядка. В частности, приимеем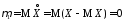для всех случайных величин.

Особое значение для практики имеет второй центральный момент 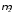, который называется дисперсией случайной величины и обозначается.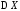

Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: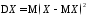. (2.11)

Для дисперсии 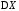справедливо также следующее выражение:

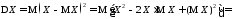
Таким образом, наряду с (2.11), имеем эквивалентное определение дисперсии 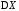: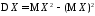. (2.12)

Дисперсия 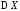характеризует степень разброса (рассеивания) значений случайной величины относительно ее среднего значения (математического ожидания).

Механическая интерпретация дисперсии. Дисперсия представляет собой момент инерции распределения масс относительно центра масс (центра тяжести, математического ожидания).

Вычисляются начальные моменты 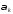по формулам, вытекающим из основной теоремы о математическом ожидании для функции:

если Х – дискретная случайная величина, то ;

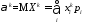если Х – непрерывная случайная величина, то .

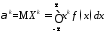Центральные моменты вычисляются по формулам, вытекающим из основной теоремы о математическом ожидании для функции:

если Х – дискретная случайная величина, то ;

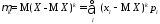если Х – непрерывная случайная величина, то .

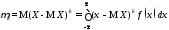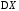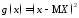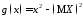Формулы для вычисления дисперсии вытекают из основной теоремы о математическом ожидании для функции, если используется формула (2.11), или для функции, если используется формула (2.12):

если Х – дискретная случайная величина, то

если Х – непрерывная случайная величина, то

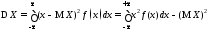
Свойства дисперсии

D1). 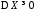,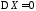тогда и только тогда, когда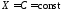п.н.

▲ Поскольку 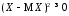для любого, тов соответствии со свойством М4) математического ожидания

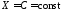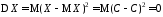Предположим, что п.н. Тогдаи. Обратно, если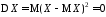, то в соответствии со свойством М4) математического ожидания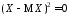п.н., а значит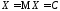п.н. ■.

D2). Дисперсия не изменяется при прибавлении к случайной величине константы: .

▲ ■.

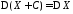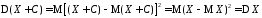D3). Константа из-под знака дисперсии выносится с квадратом: .

▲ ■.

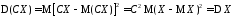Дисперсия имеет размерность квадрата случайной величины. Характеристикой рассеивания, размерность которой совпадает с размерность случайной величины, является среднее квадратическое отклонение (стандартное отклонение), определяемое как корень арифметический из дисперсии:.

Поэтому часто пишут: .

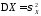Другие используемые на практике числовые характеристики положения.

Величина , определяемая равенством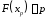, называется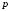 - квантилем распределения случайной величины .

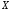Квантиль называетсямедианой распределения случайной величины 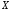. Другими словами, медиана – это значениена числовой прямой, для которого

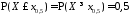
Модой распределения непрерывной случайной величины называется число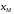, при котором плотность вероятностейдостигает максимального значения. Распределения с одной модой называютсяунимодальными, а распределения с несколькими модами – мультимодальными.

Для симметричных распределений медиана, мода и математическое ожидание совпадают.