
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
7. Формулы полной вероятности и Байеса. Пример.
Предположим,
что с данным случайным экспериментом
связана полная группа событий
 ,
вероятности которых
,
вероятности которых известны. Нас интересует некоторое
событиеА,
которое может наступить одновременно
с одним из
известны. Нас интересует некоторое
событиеА,
которое может наступить одновременно
с одним из
 .
При этом условные вероятности
.
При этом условные вероятности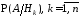 наступления событияА
при каждом
наступления событияА
при каждом
 известны. Требуется определить безусловную
вероятность
известны. Требуется определить безусловную
вероятность .
.
Представим
событие А в
виде:
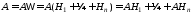 .
.
В
полученной сумме слагаемые являются
попарно несовместными:
 ,
, .
Поэтому, используя аксиому аддитивности
и правило умножения вероятностей,
получаем:
.
Поэтому, используя аксиому аддитивности
и правило умножения вероятностей,
получаем:
 .
.
Формула
 называется
формулой
полной вероятности.
В ней события
называется
формулой
полной вероятности.
В ней события
 называютсягипотезами
(так как одно из
называютсягипотезами
(так как одно из
 обязательно происходит), а вероятности
обязательно происходит), а вероятности -вероятностями
гипотез.
-вероятностями
гипотез.
Пусть,
по-прежнему, со случайным экспериментом
связано n
гипотез
 ,
вероятности которых
,
вероятности которых известны. Известно также, что гипотеза
известны. Известно также, что гипотеза сообщает событиюА
вероятность
сообщает событиюА
вероятность
 .
Предположим, что эксперимент был
произведён, и в результате событиеА
произошло. Этот факт приводит к переоценке
вероятностей гипотез
.
Предположим, что эксперимент был
произведён, и в результате событиеА
произошло. Этот факт приводит к переоценке
вероятностей гипотез
 .
Количественно этот вопрос решает
следующая формула:
.
Количественно этот вопрос решает
следующая формула: .
.
Полученная
формула называется формулой
Байеса (или
формулой гипотез). В ней
 называютсяаприорными
вероятностями гипотез (они
определяются a
priori
– до проведения опыта). Условные
вероятности
называютсяаприорными
вероятностями гипотез (они
определяются a
priori
– до проведения опыта). Условные
вероятности
 называютсяапостериорными
вероятностями гипотез
(они вычисляются a
posteriori
– после проведения опыта, когда стало
известно, что событие А
произошло).
называютсяапостериорными
вероятностями гипотез
(они вычисляются a
posteriori
– после проведения опыта, когда стало
известно, что событие А
произошло).
Пример.
По каналу связи с помехами передаются
двоичные символы {0,1}. Вероятности
искажения символов в канале (0 1,
1
1,
1 0)
одинаковы и равны0.2.
Вероятность символа 0 на входе канала
равна 0,9, а вероятность символа 1 - 0,1. На
выходе канала принят сигнал, соответствующий
1. Определить вероятность того, что на
вход канала
подавалась
также 1.
0)
одинаковы и равны0.2.
Вероятность символа 0 на входе канала
равна 0,9, а вероятность символа 1 - 0,1. На
выходе канала принят сигнал, соответствующий
1. Определить вероятность того, что на
вход канала
подавалась
также 1.
Решение.
Рассмотрим гипотезы
 =
{На входе канала связи символ 0},
=
{На входе канала связи символ 0},
 =
{На входе канала связи символ 1}.
=
{На входе канала связи символ 1}.
Очевидно,
 и по условию
и по условию ,
то есть события
,
то есть события и
и образуют полную группу событий.
образуют полную группу событий.
Пусть событие А = {На выходе канала принят символ 1}.
Тогда
по условию задачи вероятность искажения
символа 0 в канале суть условная
вероятность
 ,
а условная вероятность
,
а условная вероятность является
вероятностью неискажения в канале
символа 1. В терминах введенных обозначений
требуется найти условную (апостериорную)
вероятность
является
вероятностью неискажения в канале
символа 1. В терминах введенных обозначений
требуется найти условную (апостериорную)
вероятность .
.
Найдем вначале по формуле полной вероятности безусловную вероятность события А:
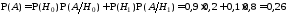 .
.
Затем,
в соответствии с формулой Байеса, находим
апостериорную вероятность
 :
:

(при
априорной вероятности
 ).
).
Очевидно,
что при этом апостериорная вероятность

(при
априорной вероятности
 ).
).
Замечание. Таким образом, даже при приеме на выходе канала связи 1 мы отдаем предпочтение в пользу 0 на входе. Это объясняется тем, что априорная вероятность 0 на входе канала существенно больше априорной вероятности 1.
8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
Предположим, что некоторый эксперимент может повторяться при неизменных условиях сколько угодно раз, и эти повторения не зависят друг от друга. В этом случае говорят о проведении последовательности независимых испытаний. Независимость испытаний при этом следует понимать в том смысле, что любые события, которые могут произойти в результате, являются независимыми в совокупности.
Простейшей является последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: успех – У (1) и неуспех – Н (0). Последовательность независимых испытаний с двумя исходами называется схемой независимых испытаний Бернулли.
Обозначим
вероятность успеха
 ,
а вероятность неуспеха
,
а вероятность неуспеха .
.
При
проведении n
независимых испытаний по схеме Бернулли
пространство элементарных событий
имеет вид:
 ,
,
а вероятности элементарных событий в силу независимости вычисляются по формуле:
 ,
,
то
есть
 .
.
В
связи с рассмотрением схемы независимых
испытаний Бернулли обычно представляют
интерес события
 ={Вn
испытаниях наступило ровно m
успехов} = =
={Вn
испытаниях наступило ровно m
успехов} = =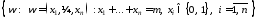 .
.
Обозначим
вероятность
 и вычислим ее. Для любого
и вычислим ее. Для любого вероятность
вероятность ,
а общее количество исходов, содержащихся
в
,
а общее количество исходов, содержащихся
в ,
равно числу способов размещенияm
единиц в последовательности длины n
из нулей и
единиц, то есть
,
равно числу способов размещенияm
единиц в последовательности длины n
из нулей и
единиц, то есть
 .
Таким образом,
.
Таким образом, .
.
Полученная формула называется формулой Бернулли. Она даёт выражение для вероятности наступления m успехов в n независимых испытаниях по схеме Бернулли с неизменной вероятностью успеха в одном испытании равной p и с вероятностью неуспеха равной q = 1 – p.
Поскольку
события
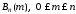 образуют полную группу событий, то
образуют полную группу событий, то
 .
Тот же результат можно получить и на
основании бинома Ньютона:
.
Тот же результат можно получить и на
основании бинома Ньютона:
Исследуем
поведение вероятностей
 в зависимости отm.
Для этого вычислим отношение:
в зависимости отm.
Для этого вычислим отношение:
 .
.
Отсюда
следует, что вероятности
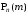 возрастают, когда
возрастают, когда
 или, что эквивалентно,
или, что эквивалентно, .
.
Вероятности
 убывают, когда
убывают, когда
 или, что эквивалентно,
или, что эквивалентно, .
.
И,
наконец,
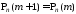 ,
если
,
если .
.
Определение.
Число успехов m
= m0,
при котором вероятности
 достигают максимума, называются
наивероятнейшим числом успехов.
достигают максимума, называются
наивероятнейшим числом успехов.
Из
проведённых рассуждений следует, что
наивероятнейшее число успехов m0
определяется из двойного неравенства:
 .
.
При этом:
Если число
 нецелое, то существует одно наивероятнейшее
число успехов:
нецелое, то существует одно наивероятнейшее
число успехов: .
.Если число
 целое, то существует два наивероятнейших
числа успехов:
целое, то существует два наивероятнейших
числа успехов: и
и .
.Если число
 целое, то
целое, то .
.
Вычисления
по формуле Бернулли при больших m
и n
весьма трудоёмкие. На практике в этом
случае используют асимптотические
приближения для вероятностей
 ,
основанные на предельных теоремах
Пуассона и Муавра-Лапласа.
,
основанные на предельных теоремах
Пуассона и Муавра-Лапласа.
