39. Теорема Хинчина. Понятие об усиленном збч.

Требование конечности дисперсии в законе больших чисел для независимых одинаково распределенных случайных величин (см. Теорему 3) связано исключительно со способом доказательства и в действительности это утверждение остается справедливым, если требовать только существование математического ожидания.

Теорема (Хинчина).

Любая последовательность независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание, подчиняется закону больших чисел, то есть.

▲ Так как сходимость по вероятности к константе эквивалентна слабой сходимости (см. лемму о связи слабой сходимости со сходимостью по вероятности), то достаточно доказать слабую сходимость

.

По теореме непрерывности эта сходимость имеет место, если и только если для любого

.

Вычислим характеристическую функцию случайной величины .

Пользуясь свойствами ихарактеристических функций, имеем:

.

Поскольку первый момент случайной величины существует, томожно разложить в ряд Тейлора в окрестности нуля:

и, следовательно, .

При , пользуясь вторым замечательным пределом, имеем:■.

В условиях теоремы Хинчина имеет место не только сходимость по вероятности , но и сходимость почти наверное.

Теорема (Усиленный закон больших чисел Колмогорова для независимых одинаково распределенных случайных величин, без доказательства).

Если - последовательность независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание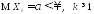, то имеет место сходимость

40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.

В математической статистике имеют дело со стохастическими экспериментами, состоящими в проведении повторных независимых наблюдений над некоторой случайной величиной , имеющей неизвестное распределение вероятностей, т.е. неизвестную функцию распределения. В этом случае множествовсех возможных значений наблюдаемой случайной величиныназываютгенеральной совокупностью, имеющей функцию распределения. Числа, являющиеся результатомповторных независимых наблюдений над случайной величиной, называютвыборкойиз генеральной совокупности иливыборочными (статистическими) данными. Число наблюденийназываетсяобъемом выборки. Основная задача математической статистики состоит в том, как по выборке, извлекая из нее максимум информации, сделать обоснованные выводы относительно вероятностных характеристик наблюдаемой случайной величины.

Замечание:Выборка является исходной информацией для статистического анализа и принятия решений о неизвестных вероятностных характеристиках наблюдаемой случайной величины. Однако на основе конкретной выборки обосновать качество статистических выводов принципиально невозможно. Для этого на выборку следует смотреть априорно как наслучайный вектор, координаты которого являются независимыми, распределенными так же как и, случайными величинами, и который еще не принял конкретного значения в результате эксперимента. Переход от выборки конкретнойк выборке случайнойбудет неоднократно использоваться далее при решении теоретических вопросов и задач для получения выводов, справедливых для любой выборки из генеральной совокупности.

В зависимости от дальнейших целей существует несколько способов представления статистических данных. Простейший из них - в виде статистического ряда:

Номер наблюдения	1 2 …
Результат наблюдения	…

Если среди выборочных значений имеются совпадающие, то статистический ряд удобнее записывать в виде таблицы, называемой таблицей частот:

Выборочные значения			…
Частоты			…
Относительные частоты			…

где - различные значения среди;- частота значения;- относительная частота значения. Очевидно, что. Поэтому совокупность парназываютэмпирическим законом распределения. Выборочные значения, упорядоченные по возрастанию, носят названиевариационного ряда:, где,.

Величина называетсяразмахом выборки.