
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
Теорема 2 (Линдеберга, ЦПТ для независимых разнораспределенных случайных величин, без доказательства).
Пусть
 - последовательность независимых
разно-распределенных случайных величин,
имеющих конечные математические ожидания
- последовательность независимых
разно-распределенных случайных величин,
имеющих конечные математические ожидания и дисперсии
и дисперсии
 при любом
при любом
 .
.
Обозначим
 - сумму первых
- сумму первых случайных величин,
случайных величин, ,
,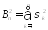 ,
,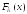 - функцию распределения случайной
величины
- функцию распределения случайной
величины ,
, .
.
Тогда,
если для любого
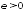 выполняется условие (условие
Линдеберга)
выполняется условие (условие
Линдеберга)
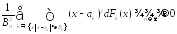 ,
,
то
при
 последовательность случайных величин
последовательность случайных величин слабо сходится к стандартному нормальному
закону распределения:
слабо сходится к стандартному нормальному
закону распределения: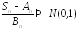
или,
что эквивалентно, последовательность
функций распределения
 сходится к функции распределения
сходится к функции распределения стандартного нормального закона
распределения равномерно по всем
стандартного нормального закона
распределения равномерно по всем :
: .
.
Эквивалентные
формы записи утверждения ЦПТ:
 ,
,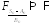 ,
,
 равномерно
по всем
равномерно
по всем
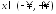 .
.
Если
все случайные величины
 являются непрерывными с плотностями
вероятностей
являются непрерывными с плотностями
вероятностей ,
,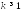 ,
то условие Линдеберга принимает вид:
для любого
,
то условие Линдеберга принимает вид:
для любого

Замечание.
Если бы в условии Линдеберга стояли
интегралы по всей прямой, то выражение
в левой части условия равнялось бы 1.
Условие Линдеберга требует, чтобы части
дисперсий случайных величин
 по области, выходящей за границы
суммарного квадратического отклонения
по области, выходящей за границы
суммарного квадратического отклонения ,
в сумме давали бы бесконечно малую
величину по сравнению с
,
в сумме давали бы бесконечно малую
величину по сравнению с .
.
Смысл условия Линдеберга.
Говорят,
что случайные величины
 равномерно асимптотически малы, если
для любого
равномерно асимптотически малы, если
для любого при
при
 .
.
Поскольку

 ,
,
то
из условия Линдеберга следует равномерная
асимптотическая малость случайных
величин
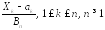 в соответствии с леммой о двух милиционерах.
Другими словами, для того, чтобы ЦПТ
имела место, все слагаемые в центрированной
и нормированной сумме
в соответствии с леммой о двух милиционерах.
Другими словами, для того, чтобы ЦПТ
имела место, все слагаемые в центрированной
и нормированной сумме должны быть равномерно асимптотически
малы в том смысле, что вероятность хотя
бы одному из них превзойти величину
должны быть равномерно асимптотически
малы в том смысле, что вероятность хотя
бы одному из них превзойти величину должна стремиться к нулю при возрастании
числа слагаемых (то есть, влияние каждого
слагаемого на всю сумму должно быть
очень мало). Заметим, что данное ограничение
касается исключительно случая
разнораспределенных слагаемых, для
одинаково распределенных слагаемых
ЦПТ выполняется без каких-либо
дополнительных предположений.
должна стремиться к нулю при возрастании
числа слагаемых (то есть, влияние каждого
слагаемого на всю сумму должно быть
очень мало). Заметим, что данное ограничение
касается исключительно случая
разнораспределенных слагаемых, для
одинаково распределенных слагаемых
ЦПТ выполняется без каких-либо
дополнительных предположений.
Задача. Показать, что для независимых одинаково распределенных случайных величин условие Линдеберга выполняется всегда.
Таким
образом, условие Линдеберга является
достаточным для справедливости ЦПТ и
выполнения условия равномерной
асимптотической малости случайных
величин
 .
Оказывается, что при наличии равномерной
асимптотической малости случайных
величин
.
Оказывается, что при наличии равномерной
асимптотической малости случайных
величин условие Линдеберга является и необходимым
для справедливости ЦПТ (это утверждение
известно как теорема Линдеберга-Феллера).
условие Линдеберга является и необходимым
для справедливости ЦПТ (это утверждение
известно как теорема Линдеберга-Феллера).
Существуют и другие достаточные условия для справедливости ЦПТ. Они, естественно, являются более ограничительными, чем условие Линдеберга, но проверять на практике их проще. Примером тому служит следующая теорема.
Теорема 3 (Ляпунова, ЦПТ для независимых разнораспределенных случайных величин).
Пусть
 - последовательность независимых
разно-распределенных случайных величин,
имеющих конечные математические ожидания
- последовательность независимых
разно-распределенных случайных величин,
имеющих конечные математические ожидания ,
дисперсии
,
дисперсии
 и центральные
абсолютные моменты
и центральные
абсолютные моменты
 порядка
порядка при некотором
при некотором
 и любом
и любом .
.
Обозначим
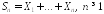 - сумму первых
- сумму первых случайных величин,
случайных величин, ,
,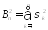 и
и .
.
Тогда,
если
 (условие Ляпунова),
(условие Ляпунова),
то
при
 последовательность случайных величин
последовательность случайных величин слабо сходится к стандартному нормальному
закону распределения:
слабо сходится к стандартному нормальному
закону распределения:
или,
что эквивалентно, последовательность
функций распределения
 сходится к функции распределения
сходится к функции распределения стандартного нормального закона
распределения равномерно по всем
стандартного нормального закона
распределения равномерно по всем :
: .
.
▲ Покажем, что условие Ляпунова является достаточным для выполнения условия Линдеберга.
Действительно,
для любого
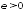

 .
.
Следовательно,
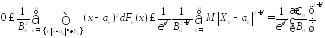 .
.
Поэтому, если выполняется условие Ляпунова, то по лемме о двух милиционерах выполняется и условие Линдеберга ■.
При ссылках на ЦПТ удобно использовать понятие асимптотической нормальности.
Определение.
Говорят, что случайная величина
 при
при асимптотически нормальна с параметрами
асимптотически нормальна с параметрами (краткая запись:
(краткая запись: ),
если закон распределения случайной
величины
),
если закон распределения случайной
величины слабо сходится при
слабо сходится при к стандартному нормальному закону
распределения:
к стандартному нормальному закону
распределения:
 .
.
С учетом этого определения утверждения Теорем 1 и 2 можно записать следующим образом.
Теорема
1.
 ;Теорема
2.
;Теорема
2.

Прикладное значение ЦПТ состоит в следующем. Если случайная величина представляет собой сумму большого числа независимых случайных величин, то можно считать, что ее закон распределения является нормальным, причем тип распределения слагаемых безразличен (при выполнении условия Линдеберга). Этим фактом и объясняется широкое распространение на практике нормального закона распределения.
Проиллюстрируем
действие ЦПТ на сумме независимых
равномерно распределенных СВ
 .
.
Обозначим
 - плотность вероятностей случайной
величины
- плотность вероятностей случайной
величины ,
, ,
, - плотность вероятностей случайной
величины
- плотность вероятностей случайной
величины .
.
С
одной стороны, плотность вероятностей
 можно найти аналитически с помощью
интеграла свертки (4.13):
можно найти аналитически с помощью
интеграла свертки (4.13): .
.
Графическая
иллюстрация этого:



С
другой стороны, поскольку
 ,
то в соответствии с ЦПТ случайная
величина
,
то в соответствии с ЦПТ случайная
величина

имеет
приблизительно стандартный нормальный
закон распределения или, что эквивалентно,
случайной величина
 является асимптотически нормальной:
является асимптотически нормальной: .
Последнее означает, что для плотности
вероятностей
.
Последнее означает, что для плотности
вероятностей справедливо приближенное равенство:
справедливо приближенное равенство:
 .
(4.19)
.
(4.19)
Оказывается,
что уже при
 ,
точность приближения в равенстве (4.19)
вполне пригодна для практического
использования и это свидетельствует о
достаточно быстрой скорости сходимости
в ЦПТ.
,
точность приближения в равенстве (4.19)
вполне пригодна для практического
использования и это свидетельствует о
достаточно быстрой скорости сходимости
в ЦПТ.
При
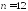 утверждение ЦПТ принимает вид:
утверждение ЦПТ принимает вид:
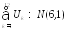 или
или
 .
(4.20)
.
(4.20)
На
последнем соотношении основан алгоритм
получения значений стандартной нормальной
случайной величины
 с
помощью значений случайной величины
с
помощью значений случайной величины ,
то есть с помощью датчика случайных
чисел:
,
то есть с помощью датчика случайных
чисел: .
.
Заметим,
что алгоритм моделирования стандартной
нормальной случайной величины с помощью
функции, обратной к функции распределения,
неприменим, поскольку функция Лапласа
 не выражается через элементарные.
не выражается через элементарные.
