
- •1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
- •Свойства операций над событиями
- •2. Классическое определение вероятности. Урновая схема. Пример.
- •3. Геометрическое определение вероятности. Пример.
- •4. Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности.
- •5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
- •6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
- •7. Формулы полной вероятности и Байеса. Пример.
- •8. Схема независимых испытаний Бернулли. Наивероятнейшее число успехов.
- •9. Понятие случайной величины (св). Функция распределения св и ее свойства.
- •10. Дискретные св. Закон распределения дискретной св.
- •11. Важнейшие дискретные св.
- •12. Непрерывные св. Плотность вероятностей и ее свойства.
- •13. Важнейшие непрерывные св.
- •14. Математическое ожидание (мо) дискретных и непрерывных св.
- •15. Основная теорема о мо. Свойства мо.
- •16. Моменты высших порядков. Дисперсия и среднеквадратическое отклонение. Свойства дисперсии.
- •17. Числовые характеристики важнейших св.
- •18. Случайные векторы. Функция распределения случайного вектора и ее свойства.
- •19. Дискретные случайные векторы. Закон распределения дискретного случайного вектора.
- •20. Непрерывные случайные векторы. Плотность вероятностей случайного вектора и ее свойства.
- •21.Равномерное распределение в области на плоскости. Равномерные распределения в прямоугольнике и в круге.
- •22. Независимость случайных величин. Условия независимости. Независимость в совокупности.
- •23.Условные законы распределения. Условная плотность вероятностей и ее свойства. Условные числовые характеристики.
- •24.Числовые характеристики случайных векторов. Корреляционная матрица и ее свойства. Понятие о моментах случайных векторов.
- •25. Теоремы о числовых характеристиках.
- •26. Некоррелированные св. Связь между некоррелированностью и независимостью. Пример.
- •27. Коэффициент корреляции, его свойства и вероятностный смысл.
- •28. Многомерное нормальное распределение и его свойства.
- •29. Функции от св и их законы распределения. Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •30. Закон распределения суммы св. Композиция (свертка) законов распределения. Пример.
- •31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •32. Закон больших чисел (збч) для последовательностей св. Теоремы Маркова и Чебышева.
- •33. Збч для последовательностей независимых одинаково распределенных св. Задача об измерениях. Теорема Бернулли и ее применение.
- •34. Характеристическая функция св и ее свойства.
- •Свойства характеристических функций
- •35.Характеристические функции важнейших св. Устойчивость нормального закона распределения.
- •Характеристические функции случайных векторов
- •36. Сходимость распределений (слабая сходимость) и ее связь со сходимостью по вероятности. Теорема непрерывности.
- •37.Центральная предельная теорема (цпт) для независимых одинаково распределенных св. Интегральная теорема Муавра-Лапласа.
- •38.Цпт для независимых разнораспределенных св: теоремы Линдеберга и Ляпунова. Смысл условия Линдеберга. Асимптотическая нормальность.
- •39. Теорема Хинчина. Понятие об усиленном збч.
- •40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.
- •41. Эмпирическая функция распределения и ее свойства.
- •42. Гистограмма и полигон частот.
- •43.Выборочные (эмпирические) числовые характеристики. Выборочное среднее и выборочная дисперсия.
- •44.Точечные оценки неизвестных параметров распределений. Требования, предъявляемые к точечным оценкам.
- •Точечные оценки. Методы нахождения точечных оценок.
- •45. Свойства выборочного среднего и выборочной дисперсии как точечных оценок мо и дисперсии соответственно.
- •46. Метод моментов получения точечных оценок. Свойства оценок, найденных по методу моментов. Пример. Метод моментов.
- •47. Метод максимального правдоподобия. Свойства оценок максимального правдоподобия. Пример.
- •48. Интервальные оценки неизвестных параметров распределений. Доверительные интервалы (ди) для мо нормально распределенной гс (при известной и неизвестной дисперсии).
- •49. Ди для дисперсии нормально распределенной гс (при известном и неизвестном мо).
- •50. Асимптотические ди для мо и дисперсии произвольно распределенной гс.
- •51. Статистические гипотезы. Критерии согласия и их характеристики.
- •52. Критерий хи-квадрат Пирсона для проверки простой гипотезы о виде распределения.
- •53. Критерий хи-квадрат Пирсона для проверки сложной гипотезы о виде распределения.
31. Неравенство Чебышева. Виды сходимости последовательностей св и связь между ними.
Есть две группы предельных теорем, объединяемых названиями: законы больших чисел и центральная предельная теорема. Законы больших чисел устанавливают факт приближения среднего арифметического случайных величин к некоторой неслучайной величине (константе). Центральная предельная теорема устанавливает факт приближения закона распределения суммы случайных величин к нормальному закону распределения.
Прежде, чем переходить к рассмотрению предельных теорем, приведем ряд понятий и фактов, необходимых для их формулировки и доказательства.
Неравенство Чебышева
Получим вначале некоторые оценки для распределений случайных величин.
Лемма.
Если неотрицательная случайная величина
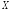 имеет конечное математическое ожидание
имеет конечное математическое ожидание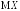 ,
то для любого
,
то для любого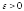 справедливо неравенство:
справедливо неравенство: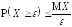 .
.
▲ Докажем лемму для непрерывной случайной
величины
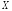 (для дискретной случайной величины
доказать самостоятельно). По определению
математического ожидания непрерывной
случайной величины
(для дискретной случайной величины
доказать самостоятельно). По определению
математического ожидания непрерывной
случайной величины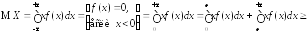
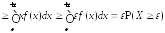 ,
,
откуда и следует утверждение леммы ■.
Следствие
(неравенство Чебышева).
Если случайная величина
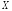 имеет конечную дисперсию
имеет конечную дисперсию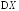 ,
то для любого
,
то для любого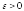 справедливы
следующие неравенства:
справедливы
следующие неравенства: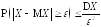 ;
(4.15)
;
(4.15)
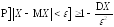 .
.
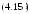
▲ В соответствии с предыдущей леммой
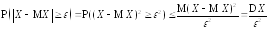 ,
,
что
доказывает неравенство (4.15). Неравенство
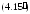 следует из (4.15) путем перехода к
противоположному событию ■.
следует из (4.15) путем перехода к
противоположному событию ■.
Неравенство
Чебышева имеет большое теоретическое
и практическое значение. Оно дает простую
оценку для вероятности отклонения
случайной величины с произвольным
законом распределения от ее математического
ожидания. Причем, если о случайной
величине, кроме ее математического
ожидания и дисперсии ничего неизвестно,
то эту оценку улучшить нельзя (существует
пример случайной величины, для которой
в (4.15) достигается равенство). Если же
есть дополнительная информация о
случайной величине (например, известен
ее закон распределения), то оценки (4.15)
и
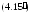 могут быть существенно улучшены.
могут быть существенно улучшены.
Пример.
Пусть случайная величина
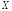 имеет нормальный закон распределения:
имеет нормальный закон распределения: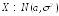 .
Тогда:
.
Тогда:
-
на основании неравенства Чебышева
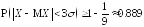 ;
;
-
в соответствии с «правилом
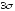 »
»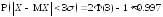 ,
,
где
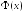 - функция Лапласа.
- функция Лапласа.
Виды сходимости последовательностей случайных величин и связь между ними
Как
и в математическом анализе, в теории
вероятностей имеют дело с различными
видами сходимости последовательностей
случайных величин. Основными среди них
являются: сходимость по вероятности,
сходимость почти наверное и сходимость
в среднем порядка
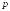 (в среднем квадратическом).
(в среднем квадратическом).
Пусть
на вероятностном пространстве
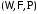 заданы последовательность случайных
величин
заданы последовательность случайных
величин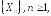 и величина
и величина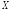 (случайная или нет).
(случайная или нет).
Определение.
Говорят, что последовательность случайных
величин
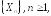 сходится по
вероятности
к величине
сходится по
вероятности
к величине
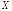 ,
если для любого
,
если для любого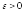
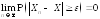
или,
что эквивалентно,
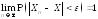
Краткое
обозначение сходимости по вероятности:
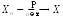 или
или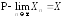 .
В математическом анализе этот вид
сходимости называется сходимостьюпо
мере.
.
В математическом анализе этот вид
сходимости называется сходимостьюпо
мере.
Определение.
Говорят, что последовательность случайных
величин
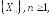 сходится
почти наверное
к величине
сходится
почти наверное
к величине
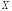 (почти всюду, с вероятностью 1), если
(почти всюду, с вероятностью 1), если
или,
что эквивалентно,
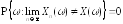 .
.
Краткое
обозначение сходимости почти наверное:
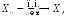
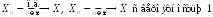 .
.
Другими
словами,
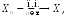 если
если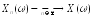 для всех
для всех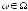 ,
за исключением, быть может,
,
за исключением, быть может,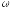 из множества
из множества ,
имеющего нулевую вероятность:
,
имеющего нулевую вероятность: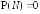 .
.
Смысл этой сходимости в математическом анализе - почти поточечная сходимость последовательности функций.
Определение.
Говорят, что последовательность случайных
величин
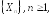 сходится к величине
сходится к величине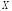 в среднем
порядка
в среднем
порядка
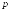 (
(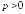 ),
если
),
если .
.
Краткое
обозначение сходимости в среднем порядка
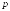 :
: (в
данном определении предполагается, что
все случайные величины обладают конечными
моментами до порядка
(в
данном определении предполагается, что
все случайные величины обладают конечными
моментами до порядка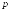 включительно).
включительно).
В
математическом анализе этот вид
сходимости называется сходимостью
в смысле
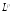 (в гильбертовом пространстве порядка
(в гильбертовом пространстве порядка
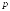 ).
).
Сходимость
в среднем порядка
 называют сходимостью в среднем
квадратическом и используют запись:
называют сходимостью в среднем
квадратическом и используют запись: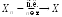 или
или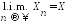 (limit
in
the
mean).
В дальнейшем мы будем иметь дело в
основном с этим видом сходимости в
среднем.
(limit
in
the
mean).
В дальнейшем мы будем иметь дело в
основном с этим видом сходимости в
среднем.
Смысл
введенных видов сходимостей
последовательностей случайных величин:
понятие предела определено только для
числовой последовательности, поэтому
случайность под знаком предела должна
быть ликвидирована. Это делается в
приведенных определениях либо с помощью
вероятности, либо с помощью математического
ожидания со своим понятием близости
между
 и
и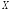 .
.
Лемма (связь между видами сходимостей).
а)
Если последовательность случайных
величин
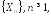 сходится к величине
сходится к величине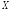 почти наверное, то она сходится к этой
величине и по вероятности:
почти наверное, то она сходится к этой
величине и по вероятности: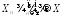

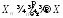 .
.
б)
Если последовательность случайных
величин
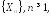 сходится к величине
сходится к величине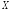 в среднем порядка
в среднем порядка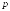 (
(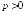 ),
то она сходится к этой величине и по
вероятности:
),
то она сходится к этой величине и по
вероятности: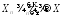

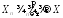 .
.
▲ а)
Если
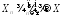 ,
то по определению сходимости почти
наверное на множестве
,
то по определению сходимости почти
наверное на множестве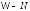 (
(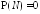 ),
начиная с некоторого
),
начиная с некоторого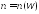 ,
при любом
,
при любом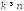 и для любого
и для любого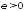 справедливо неравенство:
справедливо неравенство: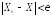 .
Другими словами,
.
Другими словами,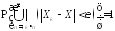
или,
переходя к противоположному событию:
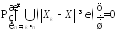 .
(4.16)
.
(4.16)
Покажем,
что равенство (4.16) эквивалентно тому,
что
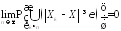 .
(4.17)
.
(4.17)
Действительно,
поскольку при любом
 :
: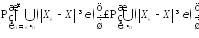 ,
,
то,
переходя в обеих частях данного
неравенства к пределу при
 ,
получаем, что из (4.17) следует (4.16), так
как вероятность не может быть отрицательной
(лемма о двух милиционерах).
,
получаем, что из (4.17) следует (4.16), так
как вероятность не может быть отрицательной
(лемма о двух милиционерах).
Для
доказательства того, что из (4.16) следует
(4.17), рассмотрим события
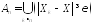 .
Поскольку
.
Поскольку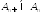 и
и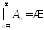 в соответствии с (4.16), то
в соответствии с (4.16), то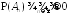 в силу аксиомы непрерывности вероятности
Р4).
в силу аксиомы непрерывности вероятности
Р4).
Для
окончательного доказательства утверждения
а) леммы достаточно заметить, что для
любого
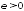 в соответствии с (4.17)
в соответствии с (4.17)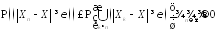 .
.
Поэтому
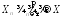 (в соответствии с леммой о двух
милиционерах).
(в соответствии с леммой о двух
милиционерах).
б)
Зафиксируем
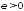 .
Тогда в силу неравенства Чебышева для
любого
.
Тогда в силу неравенства Чебышева для
любого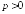
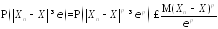 .
.
Поэтому,
если
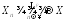 ,
то
,
то и, следовательно, для любого
и, следовательно, для любого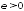
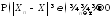 (снова в соответствии с леммой о двух
милиционерах) ■.
(снова в соответствии с леммой о двух
милиционерах) ■.
Замечание. Из леммы следует, что сходимость по вероятности является слабейшей из всех введенных трех видов сходимостей последовательностей случайных величин. Обратные импликации в утверждениях а) и б) леммы, вообще говоря, неверны (соответствующие примеры можно найти в учебнике А.А. Боровкова «Теория вероятностей»).
