MKE

Министерство образования и науки

Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»

(СГАУ)

Кафедра конструкции и проектирования

двигателей летательных аппаратов.

Расчётно-графическая работа

по методу конечных элементов (МКЭ).

Выполнил: студент группы 2204

Шкоков И.О.

Проверил: преподаватель

Уланов А.М.

Самара 2012

Содержание

Реферат_________________________________________________________ 3

• Идея метода

• Преимущества и недостатки

• История развития метода

• Системы анализа, основанные на методе

Исходные данные________________________________________________ 6

Задание граничных условий_______________________________________ 7

Построение векторов перемещений и сил____________________________ 7

Построение матриц жёсткости отдельных элементов___________________8

Построение общей матрицы жёсткости______________________________ 11

Решение________________________________________________________ 12

Заключение_____________________________________________________ 13

Список литературы______________________________________________ 14

Расчётная работа: 15 страниц, 1 рисунок, 5 источников

ВЕКТОР ПЕРЕМЕЩЕНИЯ, ВЕКТОР НАГРУЗОК, МАТРИЦА ЖЁСТКОСТИ, ОБЩАЯ МАТРИЦА ЖЁСТКОСТИ, КОЭФФИЦИЕНТ ПУАССОНА, КОЭФФИЦИЕНТ МАТРИЦЫ D, ТРАНСПОНИРОВАННАЯ МАТРИЦА, УЗЕЛ, КОНЕЧНЫЙ ЭЛЕМЕНТ

Реферат

Метод конечных элементов (МКЭ) – численный метод решения задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Идея метода

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики – общего метода исследования систем путём их расчленения.

Преимущества и недостатки

Метод конечных элементов, по словам специалистов, «большая пушка» - метод конечных разностей и проще в реализации, и быстрее. Зато у МКЭ есть свои преимущества, проявляющиеся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.

Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимость от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), и последний бастион на пути к полностью автоматическим конечноэлементным САПР пал

История развития метода

Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах (идея МКЭ была разработана советскими учёными ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развития). Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея – Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1068 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конечных элементов.

Системы анализа, основанные на методе

Наиболее распространёнными вычислительными системами, основанными на методе конечных элементов, являются:

ANSYS – универсальная систем КЭ анализа с встроенным пре-/постпроцессором;

FEM Models – система конечно-элементного анализа, преимущественно для решения геометрических задач;

MSC.Nastran – универсальная систем КЭ анализа с встроенным пре-/постпроцессором MSC.Patran;

ABAQUS – универсальная система КЭ анализа с встроенным пре-/постпроцессором;

Impact - универсальная система КЭ анализа с встроенным пре-/постпроцессором;

NEiNastran – универсальная система КЭ анализа с встроенным пре-/постпроцессором FEMAP;

NXNasrtan – универсальная система КЭ анализа с пре-/постпроцессором FEMAP;

SAMCEF - универсальная система КЭ анализа с пре-/постпроцессором SAMCEF Field.

Temper-3D – система КЭ анализа для расчёта температурных полей в трёхмерных конструкциях (теплотехнический расчёт).

COMSOL Multiphysics – универсальная система КЭ анализа с пре-/постпроцессором.

NX Nastran – универсальная система МКЭ анализа.

Zebulon – универсальная система МКЭ анализа с расширенной библиотекой нелинейных моделей материалов.

Исходные данные

Ширина (a) = 0,2 м

Высота (b) = 0,4 м

Толщина (h) = 0,01 м

Сосредоточенная сила (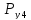) = 25000 Н

Распределённая сила (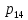) = 40000

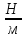
Модуль жёсткости материала (E) = 2·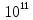 Па

Коэффициент Пуассона (µ) = 0,33

Вариант разбивки:

Пусть глобальная система координат, в которой будут производиться все расчёты, находится в узле №1. Всего данная система имеет восемь степеней свободы: перемещения вдоль осей x и y в каждом из узлов.

Задание граничных условий

Перемещения в узлах №3 и №4 отсутствуют по условии, т.е. 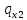= = 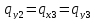0. Однако при этом в узлах №3 и №4 будут действовать неизвестные реакции

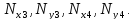
На систему также действуют внешние силы. В узле №2 действует направленная вверх сила 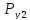, а вдоль линии 2-4 приложена равномерная погонная нагрузка 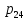(нагрузка вдоль линии имеет размерность Н/м).

Для дальнейшего расчёта погонную нагрузку необходимо привести к узлам. В силу её равномерности, она распределена поровну между узлами, и приведение можно выполнить по следующей зависимости:

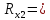
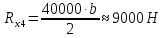
Для расчёта потребуются модуль жёсткости материала (параметры даны для стали) E = 2·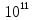 Па и коэффициент Пуассона µ = 0,33.

Построение векторов перемещений и сил

С учётом вышеизложенного, вектора перемещений и глобальных реакций всех узлов можно записать в виде

,

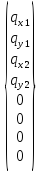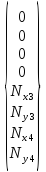
Тогда общий вектор нагрузок, приходящихся на узлы:

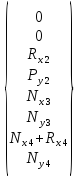
Построение матриц жёсткости отдельных элементов

Построим матрицу жёсткости на основе энергетического метода. Определим площадь каждого конечного элемента 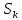. В данном случае

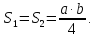
Далее найдём значения коэффициентов матрицы [D]

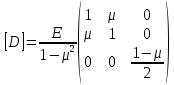
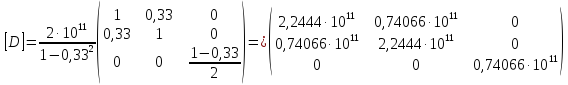
Данная матрица одинаково для всех элементов, и все её коэффициенты являются константами. Она выведена из обобщённого закона Гука.

На следующем шаге решения найдём значения коэффициентов матриц [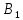] и [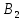], которые определяют связь геометрических характеристик внутри конечных элементов, вследствие чего для каждого элемента существует уникальная матрица [B]. Она состоит из разности координат узлов, входящих в конечный элемент. Запишем координаты узлов:

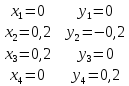
Тогда матрицы [B] для обоих конечных элементов запишутся в виде:

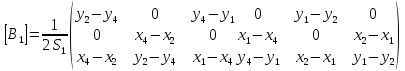
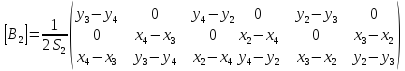
Построим транспонированную матрицу [B]:

;

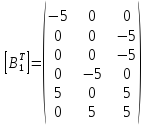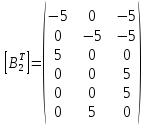
Тогда матрицы жёсткости первого и второго элементов запишутся в виде:

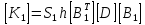
Итоговая матрица жёсткости каждого элемента может быть представлена в виде:

,

где верхний индекс обозначает номер конечного элемента. Элементы справа и слева относительно главной диагонали должны быть одинаковы. Таким образом, левый нижний угол должен быть зеркальным отражением верхнего правого с осью симметрии, проходящей через главную диагональ (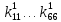) Так можно проверить правильность построения матрицы.

Построение общей матрицы жёсткости

Построим общую матрицу жёсткости [K], для чего необходимо записать уравнения равновесия для каждого узла. Т.е. сумма всех внутренних реакций в каждом узле должна быть равна нулю. При этом следует учесть, что узлы №2 и №4 принадлежат только одному конечному элементу (соответственно первому и второму). А узлы №1 и №3 принадлежат обоим конечным элементам.

В первом элементе порядок узлов №1-2-3. Поэтому для записи уравнения равновесия первого узла используем только первые две строки матрицы [К₁]. Затем разделим выбранные строки матрицы [K₁] на несколько квадратных матриц размерностью 2х2. Поскольку узел №2 принадлежит только одному элементу, то 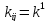, где i, j – номер строки и столбца матрицы жёсткости. Запишем все силы, действующие в узле №2.

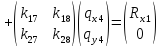
Нулевая матрица для перемещений третьего узла взята потому, что узел №4 не входит в первый конечный элемент.

Узел №3 принадлежит двум конечным элементам, поэтому его матрица жёсткости записывается сложнее. Для её записи воспользуемся третьей и четвёртой строками матрицы [К₁] и первой и второй строками матрицы [K₂], соответствующих узлу №3. Значения коэффициентов в матрицах сложим с учётом порядка узлов в элементах. Запишем матрицу сначала в общем виде

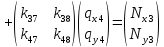(14)

Затем через коэффициенты матриц К₁ и К₂.

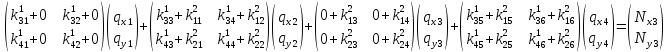(15)

Нули в первой матрице записаны потому, что узел №2 не входит во второй конечный элемент, аналогично, нули в третьей матрице объясняются тем, что узел №4 не входит в первый конечный элемент.

Аналогично получим уравнения для узлов №3 и №4.

Решение

Общая матрица жёсткости выглядит следующим образом

Поскольку перемещения узлов №3 и №4 равны нулю, перемещения узлов №1 и №2 определим из 1,2 и 3,4 строк разрешающей системы уравнений.

Решив данную систему методом Крамера, найдём корни:

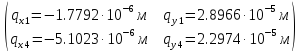
Найдём неизвестные реакции в узлах №3 и №4, подставив в общую матрицу жёсткости найденные перемещения узлов:

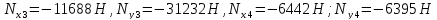
Заключение

В данной работе был проведён расчёт реакций в узлах системы, разбитой на 2 конечных элемента.

При выбранном варианте закрепления и распределении нагрузок в системе, были определены реакции в закреплённых узла 3 и4:

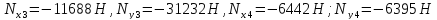
Список использованной литературы

1. Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. – М.: Мир, 1984

2. Деклу Ж. Метод конечных элементов: Пер. с франц. – М.: Мир, 1976

3. Зенкевич О. Метод конечных элементов в технике – М.: Мир, 1975

4. Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. – М.: Мир, 1986

5. Сегерлинд Л. Применение метода конечных элементов – М.: Мир, 1979. – 392 с.