Особенности расчета планетарных передач Характеристика и применение

Планетарными называют передачи, включающие в себя зубчатые колеса с перемещающимися осями (рис.10.1,а). Передача состоит из центрального колеса  с наружными зубьями, центрального колеса b с внутренними зубьями и водила Н, но котором укреплены оси сателлитов g.

Сателлиты вращаются вокруг своих осей и вместе с осью вокруг центрального колеса, т.е. совершают движение, подобное движению планет. Отсюда название – планетарные передачи.

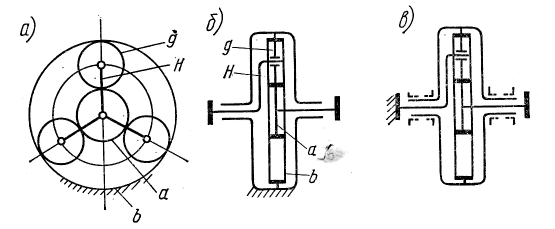
При неподвижном колесе b (рис.10.1,б) движение может передаваться от  к Н или от Н к ; при неподвижном водиле (рис.10.1,в) – от  к b или от b к .

Рис.10.1

При всех свободных звеньях одно движение можно раскладывать на два или два соединять в одно. Например, от b к  и Н, от  и Н к b и т.п. В этом случае передачу называют дифференциальной.

Широкие кинематические возможности планетарной передачи являются одним из основных ее достоинств и позволяют использовать передачу как редуктор с постоянным передаточным отношением; как коробку скоростей, передаточное отношение в которой изменяется путем поочередного торможения различных звеньев; как дифференциальный механизм.

Вторым достоинством планетарной передачи является компактность и малая масса. Переход от простых передач к планетарным позволяет во многих случаях снизить массу в 2 – 4 и более раз. Это объясняется следующим:

1. Мощность передается по нескольким потокам, число которых равно числу сателлитов (три на рис.10.1). При этом нагрузка на зубья в каждом зацеплении уменьшается в несколько раз.

2. Внутреннее зацепление (g и b) обладает повышенной нагрузочной способностью, так как у него больше приведенный радиус кривизны в зацеплении.

3. Планетарный принцип позволяет получать большие передаточные отношения (до тысячи и больше) без применения многоступенчатых передач.

4. Малая нагрузка на опоры, так как при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. Это снижает потери и упрощает конструкцию опор.

К недостаткам планетарных передач относятся повышенные требования к точности изготовления и монтажа.

Кинематика

При исследовании кинематики планетарных передач широко используют метод остановки водила – метод Виллиса.

Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм (см.рис.10.1,в), представляющий собой простую передачу, в которой движение передается от  к b через паразитное колесо g . Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кинематику передачи, изображенной на рис.10.1. Условимся приписывать частотам вращения индекс звена (n_, n_H и т.д.), а передаточные отношения сопровождать индексами в направлении движения и индексом неподвижного звена. Например, - означает передаточное отношение от к Н при неподвижном b. Для обращенного механизма

, (10.1)

так как сателлит является здесь паразитным колесом.

В планетарных передачах существенное значение имеет знак передаточного отношения. Условимся, что при i > 0 – вращение ведущего и ведомого звеньев происходит в одном направлении; при i < 0 – вращение противоположное. В рассматриваемом примере колеса  и b вращаются в разных направлениях, а поэтому < 0.

Переходя к реальному механизму, у которого в большинстве случаев практики колесо b закреплено,  - ведущее и Н – ведомое, на основе формулы (10.1) при n_b = 0 получаем: