4. Проверочный расчет на усталость по изгибу

Из предыдущих расчетов:

Y_β – коэффициент, учитывающий наклон зубьев.

Согласно рекомендации [1],Y_β=1, при β=0;

Y_Σ – коэффициент, учитывающий перекрытие зубьев.

Согласно рекомендации [1] для прямозубых колес,Y_Σ=1;

Коэффициент формы зуба

Согласно рекомендации [1], для z₁=29, седьмой степени точности и X₁=0:

Согласно рекомендации [1], для z₂=29, седьмой степени точности и X₂=0:

Расчетное напряжение по изгибу:

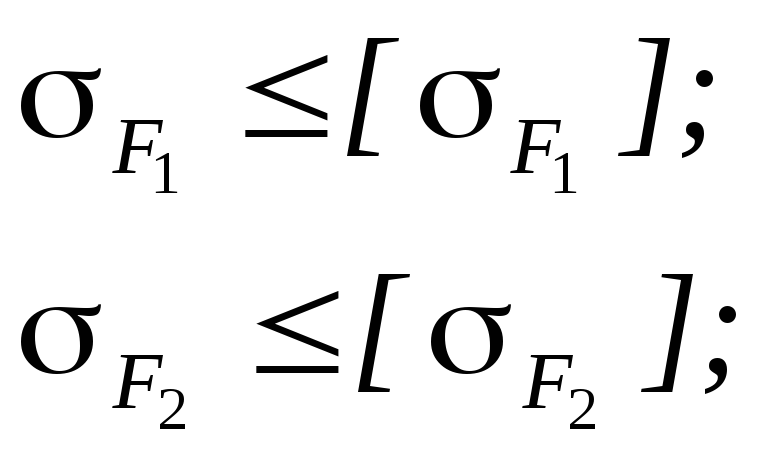Значит расчет произведен верно.

5. Проверочный расчет передачи на статическую прочность при перегрузках

Из предыдущих расчетов:

σ_H=1108 Мпа; σ_F=412,579 Мпа; T₁/T_1max=K_g=1.25; сталь 12Х4Н4А; термообработка – цементация; σ_В=1200 МПа; HRC=60,5.

Согласно рекомендации [1], для цементации, принимаем [σ_H]_max=40∙HRC;

[σ_H]_max=40∙HRC=40∙60.5=2420 МПа;

т.к. , значит расчет произведен верно.

Согласно рекомендации [1], при HB>350,

т.к. , значит расчет произведен верно.

6. Определение геометрических размеров передачи

Из предыдущих расчетов:

Делительное межосевое расстояние определяется по формуле:

Межосевое расстояние а_w=a=163.5 мм.

Делительные диаметры:

Начальные диаметры:

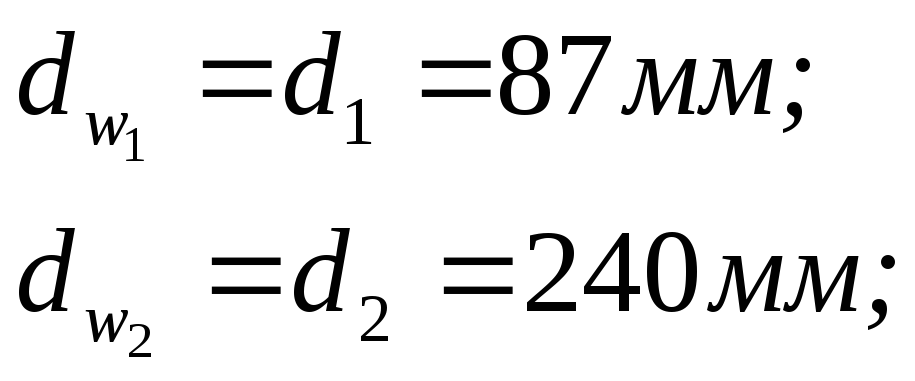
Диаметры вершин зубьев:

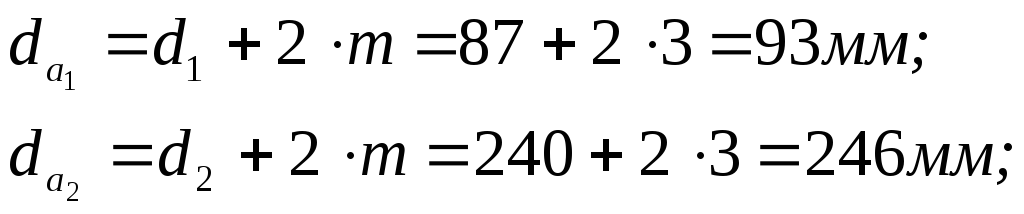
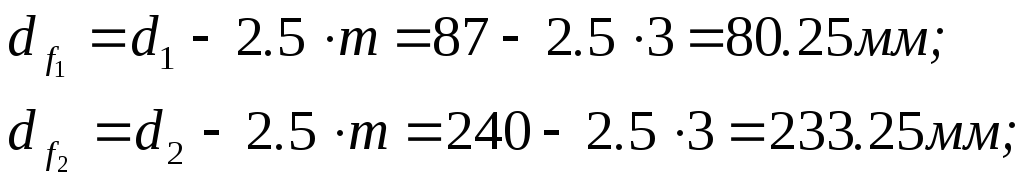
Угол рейки α_t производящей рейки в сечении перпендикулярном к оси сцепляющегося с ней зубчатого колеса:

Угол зацепления:

;

Основной угол наклона β_b:

5. Расчет планетарной передачи.

1. Определение основных параметров планетарной передачи из условий контактной прочности

Из предыдущих расчетов известно:

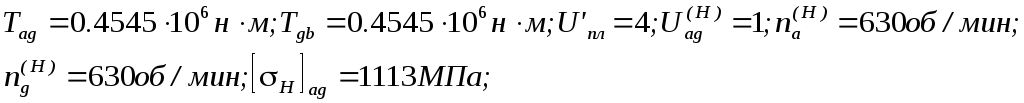
Согласно рекомендации [2] принимаем K`=1,3;

Так как U`_пл=4, то

Принимаем b_w=54 мм.

Тогда согласно рекомендации [2] принимаем K_β=1,1;

Окружная скорость:

;

Тогда согласно рекомендации [2] принимаем K_v=1,15;

К=K_β∙K_v=1.1∙1.15=1.265

Так как , то это значит, что расчет произведен верно.

2. Определение модуля зацепления

Из предыдущих расчетов:

Согласно рекомендации [2], принимаем m_min=2.5мм;

Согласно рекомендации [2], принимаем

По ГОСТ 9563-60 принимаем m=3 мм.

Округляем до z₁=30;

Согласно рекомендации [2] Y_F=3.8

значит расчет произведен верно.

3. Подбор чисел зубьев и уточнение передаточного отношения.

Из предыдущих расчетов:

z_a=30;

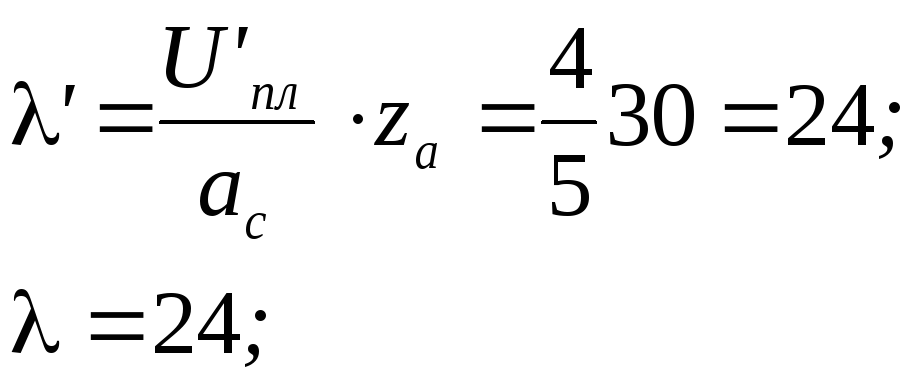
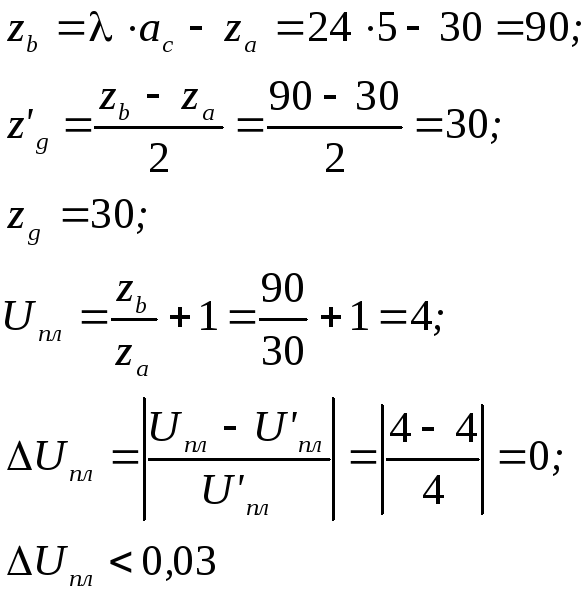
4. Определение геометрических размеров передачи.

Из предыдущих расчетов:

Межосевое расстояние:

Делительные и начальные диаметры:

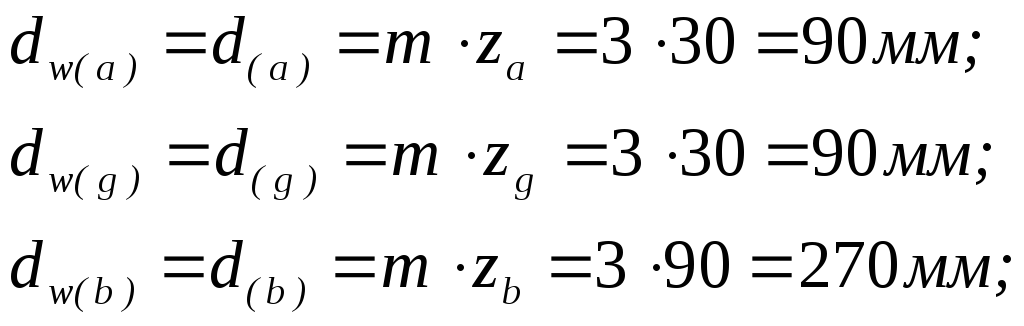
Диаметры вершин зубьев:

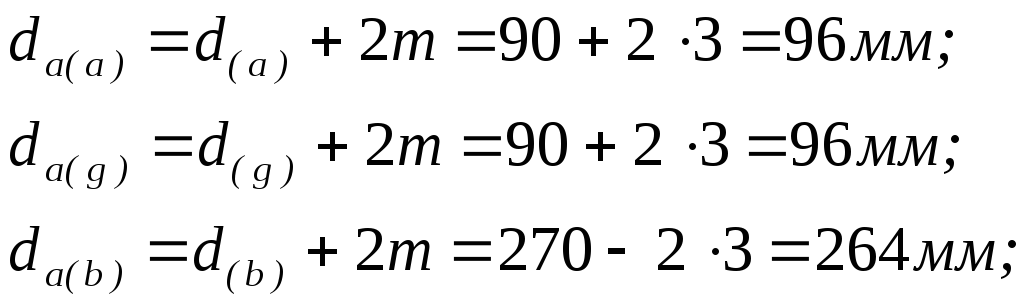
Нормальная толщина зуба:

5. Определение ширины коронки «b_w» центрального колеса «b».

Из предыдущих расчетов:

Коэффициент формы зуба:

Рабочая ширина венца зубчатого колеса из расчета на изгибную прочность:

Коэффициент торцевого перекрытия:

Коэффициент, учитывающий суммарную длину контактных линий:

Рабочая ширина венца зубчатого колеса из расчета на контактную прочность:

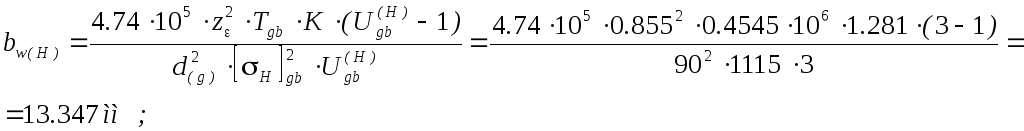Так как , то ;

Округляем до целого ;

6. Проверочный расчет передачи на контактную прочность

Из предыдущих расчетов:

Согласно рекомендации [2], т.к. принимаем:

,

Тогда

Так как , значит расчет произведен верно.

7. Проверочный расчет передачи на усталость по изгибу

Из предыдущих расчетов:

Согласно рекомендации [2], для z_a=z_g=30 принимаем

Тогда изгибные напряжения:

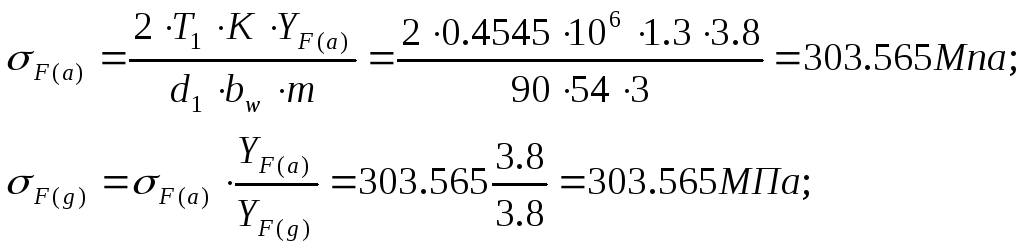
Так как, значит расчет произведен верно.

2.5.8 проверочный расчет передачи на статическую прочность при перегрузках.

Из предыдущих расчетов: , .

Определим максимальное расчетное контактное напряжение

, где , .

Следовательно, получим: .

Определим максимальное контактное напряжение исходя из условий обработки. При цементации имеем

- условие выполняется.

Определим максимальное допустимое напряжение по изгибу :

,

.

Определим максимальное допустимое напряжение по изгибу . При имеем: .

- условие выполняется.

Определение усилия в зацеплениях.