Метод наименьших квадратов

Метод наименьших квадратов

Пусть требуется установить функциональную зависимость между переменными х, у по результатам экспериментальных исследований, приведенных в таблице:

		…
		…

Нужно подобрать функцию так, чтобы ее значения были как можно более близкими к экспериментальным значениям. Выбор функции зависит от характера расположенных на плоскости экспериментальных точек.

Пример:

Погрешность, возникающая при замене экспериментальных значений на значения функции , равна в каждой точке .

В МНК коэффициенты функции f(x) подбираются из следующего условия: сумма квадратов погрешностей по всей совокупности экспериментов принимает минимальное значение:

.

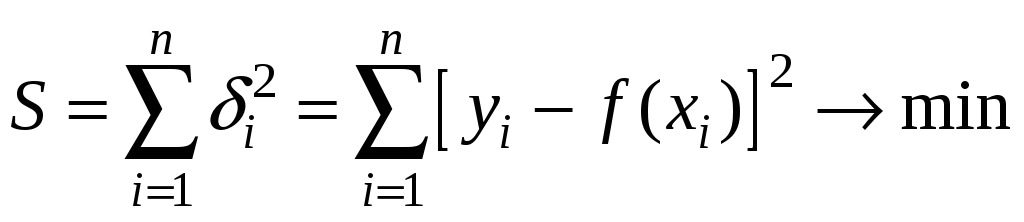Обычно рассматривают несколько видов функций f(x) выбирают ту функцию, для которой суммарная погрешность 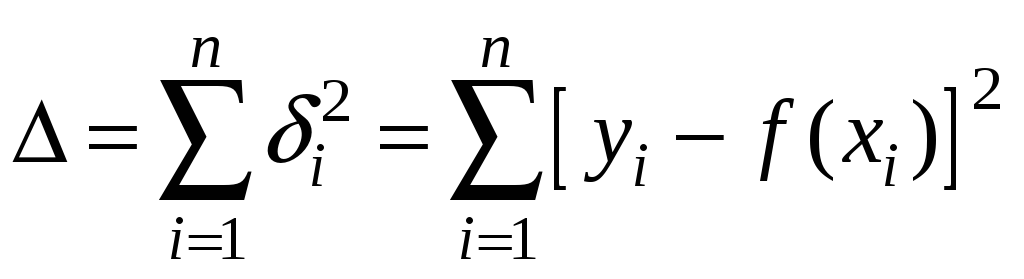окажется наименьшей.

Рассмотрим основные виды функций , используемые в МНК.

1. Линейная зависимость.

Пусть , тогда необходимо найти min функции двух переменных: .

По необходимому условию экстремума обе частные производные этой функции двух переменных должны быть равны нулю:

.

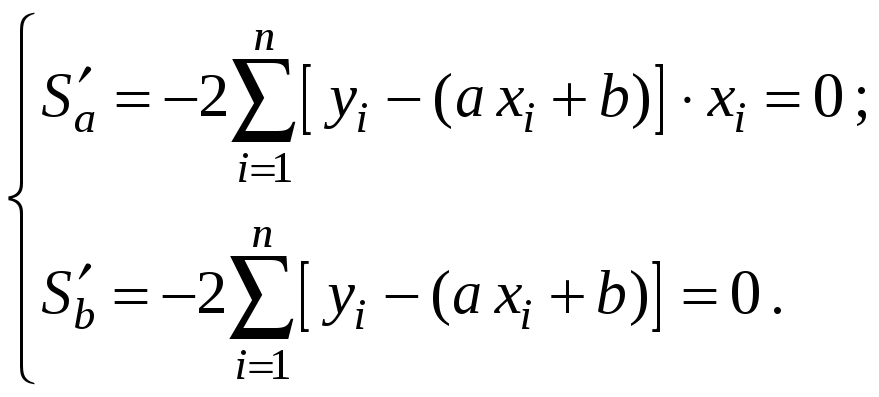Раскрывая скобки, получим систему для определения неизвестных параметров a и b:

.

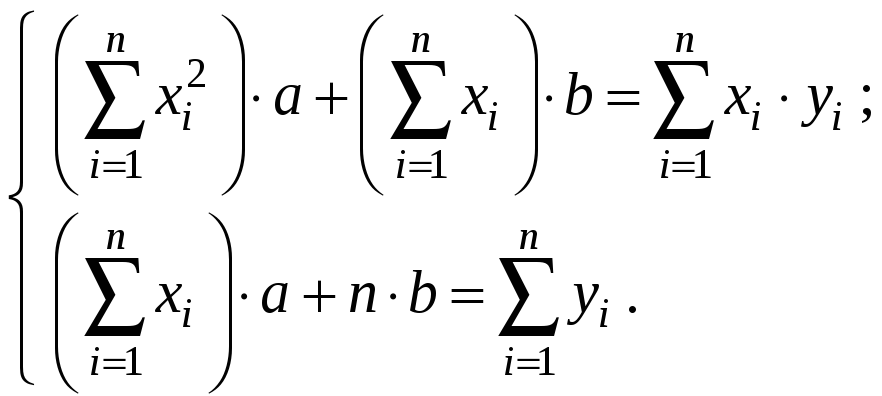Значения коэффициентов при неизвестных a и b определяем из первоначальной таблицы как соответствующие суммы значений переменных х, у .

Решая эту систему относительно коэффициентов a и b:, получим:

,

.

Убедимся, что в точке функция S(a,b) имеет минимум.

Составим матрицу Гессе и найдем ее главные миноры:

,

Так как главные миноры матрицы Гессе положительны, то по критерию Сильвестра матрица положительно определена и квадратичная форма второго дифференциала , соответствующая этой матрице, принимает только положительные значения.

Из условия следует, что - точка минимума.

Если коэффициенты линейной функции найдены, можно вычислить суммарную погрешность: .

II. Показательная функция .

Сведем этот случай к линейной функции.

1. Логарифмируем уравнение: .

2. Логарифмируем таблицу:

			…
			…

Обозначим , , тогда

3. Найдем коэффициенты А и b аналогично первому случаю линейной функции:

.

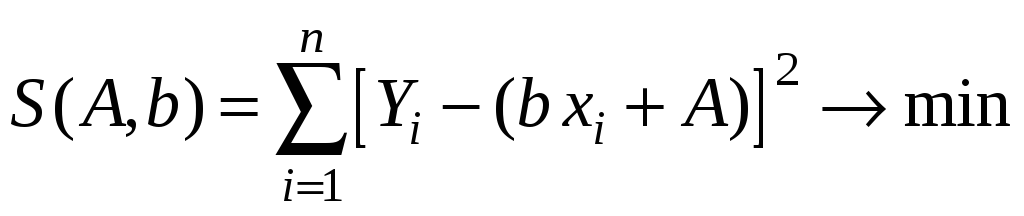Дальнейшие вычисления провести самостоятельно аналогично первому пункту. Окончательное значение коэффициента а определить по формуле .

Суммарная погрешность равна .

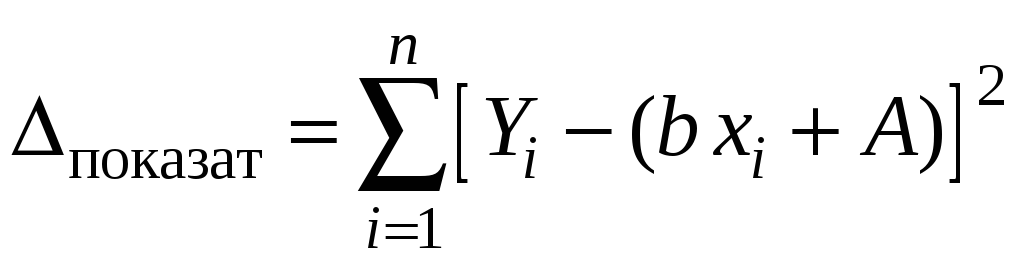III. Степенная функция .

Поступим аналогично показательной функции.

1. Логарифмируем уравнение: 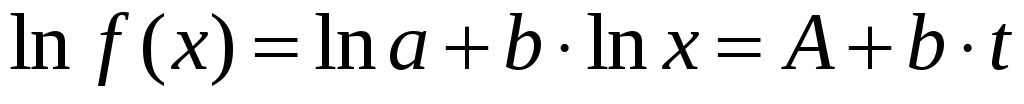, получим - линейную функцию.

2. Логарифмируем таблицу:

			…
			…

3. Обозначим . Тогда .

Найдем коэффициенты и b аналогично первому случаю:

.

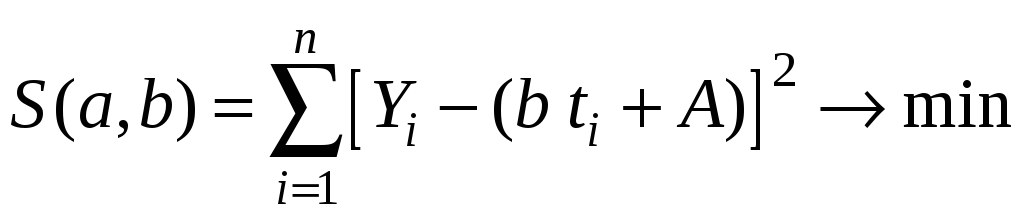Дальнейшие вычисления провести самостоятельно аналогично первому пункту. Окончательное значение коэффициента а определить по формуле .

Суммарная погрешность равна .

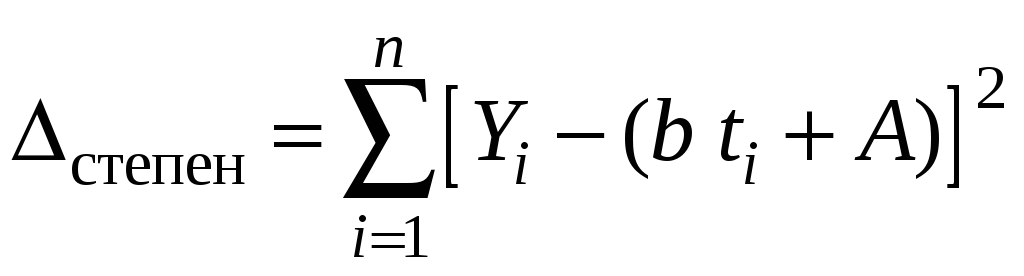IV. Квадратичная функция .

Условие метода наименьших квадратов имеет вид:

.

Аналогично линейной функции составляется система трех уравнений , из которой находятся коэффициенты a, b и с:

Запишем систему в развернутом виде:

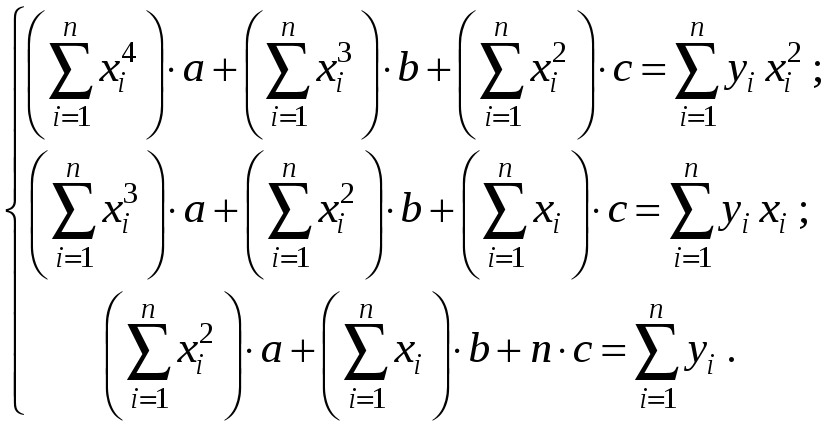
Эта система имеет единственное решение. Кроме того, можно доказать, что коэффициенты, получаемые методом наименьших квадратов, всегда определяют именно минимум функции .

Суммарная погрешность .