
Лекция_6
.pdf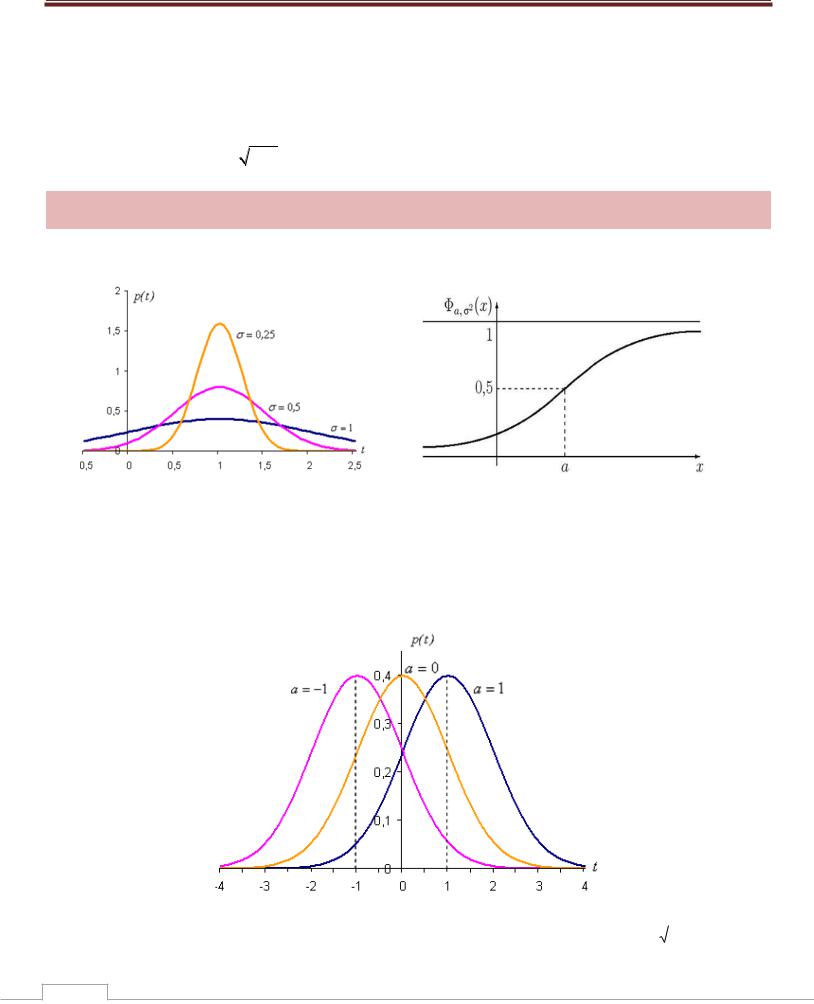
Занятие 11-12
Непрерывные случайные величины (продолжение)
§5. Нормальное распределение.
Определение 1. Нормальным законом распределения (закон Гаусса) называют распределение НСВ X , если
|
|
|
1 |
|
|
|
( x M )2 |
|
|
|
|
|
|
f (x) |
|
|
e |
2 2 |
, |
где M , - заданные константы ( 0) |
|
||||
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
||||||
Можно показать, что для такой случайной величины |
M ( X ) M |
D( X ) 2 т.е. |
( X ) |
|||||||||
Термин «нормальный» не совсем удачный. Если закон распределения другой, то это не значит, что он «ненормальный».
Графиком функции f (x) является «колокол» (гауссова кривая) с вершиной в точке x M . Чем больше, тем менее крутой «колокол»:
Для сравнения пунктиром на рисунках изображены кривые нормального распределения. График функции распределения НСВ, имеющей нормальный закон распределения: кривая симметрична относительно прямой x a М
Определение 2. Общим называют нормальное распределение с произвольными параметрами M
и ( 0) .
Нормированным называют нормальное распределение при M 0 и 1
|
|
|
1 |
|
|
|
x2 |
Плотность нормированного распределения обозначается ( X ) и равна |
(x) |
|
|
|
|
||
|
|
|
e |
2 |
|||
|
|
|
|||||
2 |
|
|
|||||
|
|
|
|
|
|
|
|
1
Занятие 11-12
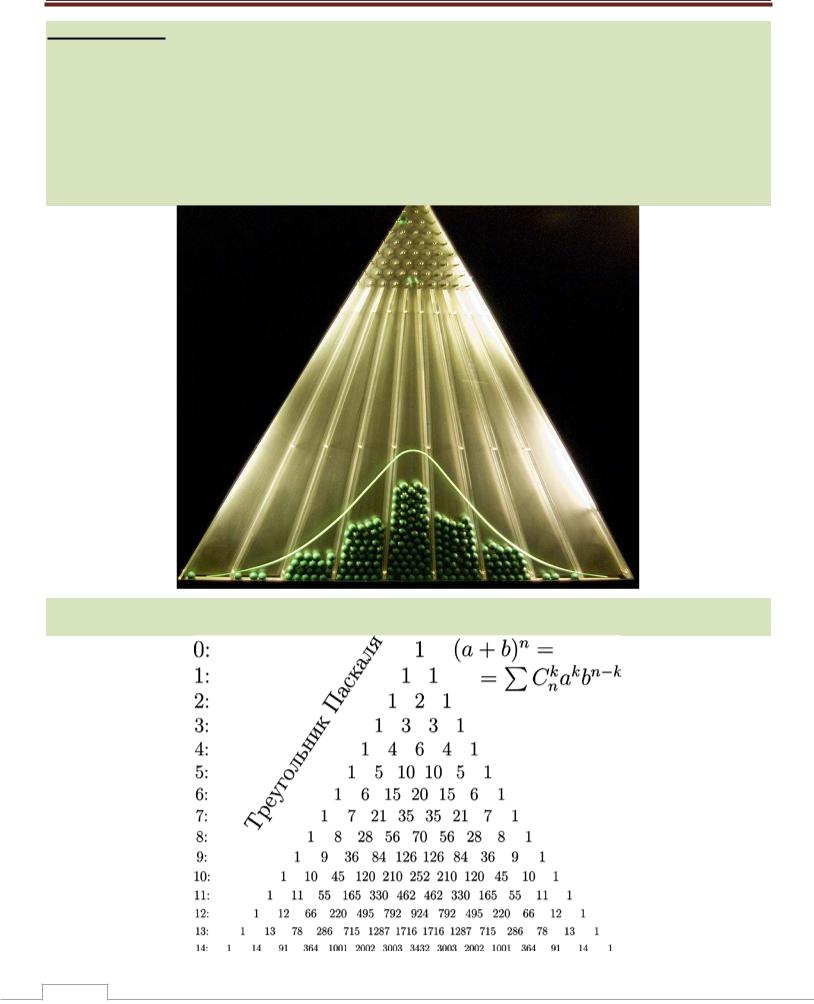
оска альтона — устройство, изобретѐнное английским учѐным Фрэнсисом Гальтоном (первый экземпляр изготовлен в 1873 году).
Доска Гальтона представляет собой ящик с прозрачной передней стенкой. В заднюю стенку в шахматном порядке вбиты штырьки, образующие треугольник. Сверху в ящик через воронку (выход из которой расположен ровно посередине между левой и правой стенками) кидаются шарики. В идеальном случае сталкиваясь со штырьком, шарик каждый раз с одинаковой вероятностью может повернуть либо направо, либо налево. Нижняя часть ящика разделена перегородками (число которых равно числу штырьков в нижнем ряду), в результате чего шарики, скатываясь на дно ящика, образуют столбики, которые тем выше, чем ближе к середине доски (при достаточно большом числе шариков внешний вид столбиков приближается к кривой нормального распределения).
Если нарисовать на задней стенке треугольник Паскаля, то можно увидеть, сколькими путями можно добраться до каждого из штырьков (чем ближе штырѐк к центру, тем больше число путей).
2

Занятие 11-12
лез Паскаль 19 июня 1623, Клермон-Ферран, Франция — 19 августа 1662, Париж, Франция) — французский математик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счѐтной техники, автор основного закона гидростатики.
Функция распределения нормированного распределения обозначается F0 (x) и равна
|
1 |
x |
|
t2 |
|
|
|
|
|
||||
F (x) |
|
2 |
e 2 dt |
|||
|
|
|
||||
0 |
|
|
|
|
|
|
Эта функция затабулирована.
Функция распределения общего нормального распределения |
F (x) может быть вычислена через F0 (x) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) F ( |
x M |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
x2 |
|||||
|
Функцией Лапласа называется функция (x) |
|
|
e |
|
|
|
|||||||||||||||||||||||||||||||||
Определение 3. |
|
2 dx |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
Она является нечетной, |
т.е. ( x) (x) , возрастающей, |
|
(0) 0 и |
|
|
|
|
( |
) |
|||||||||||||||||||||||||||||||
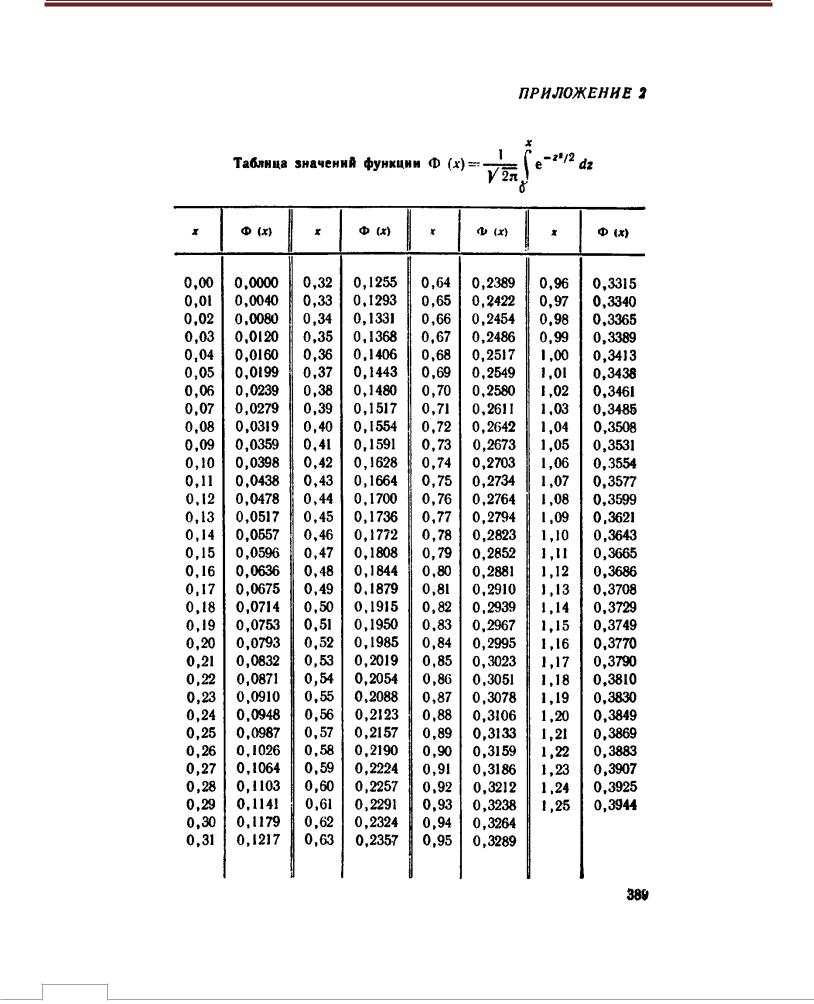
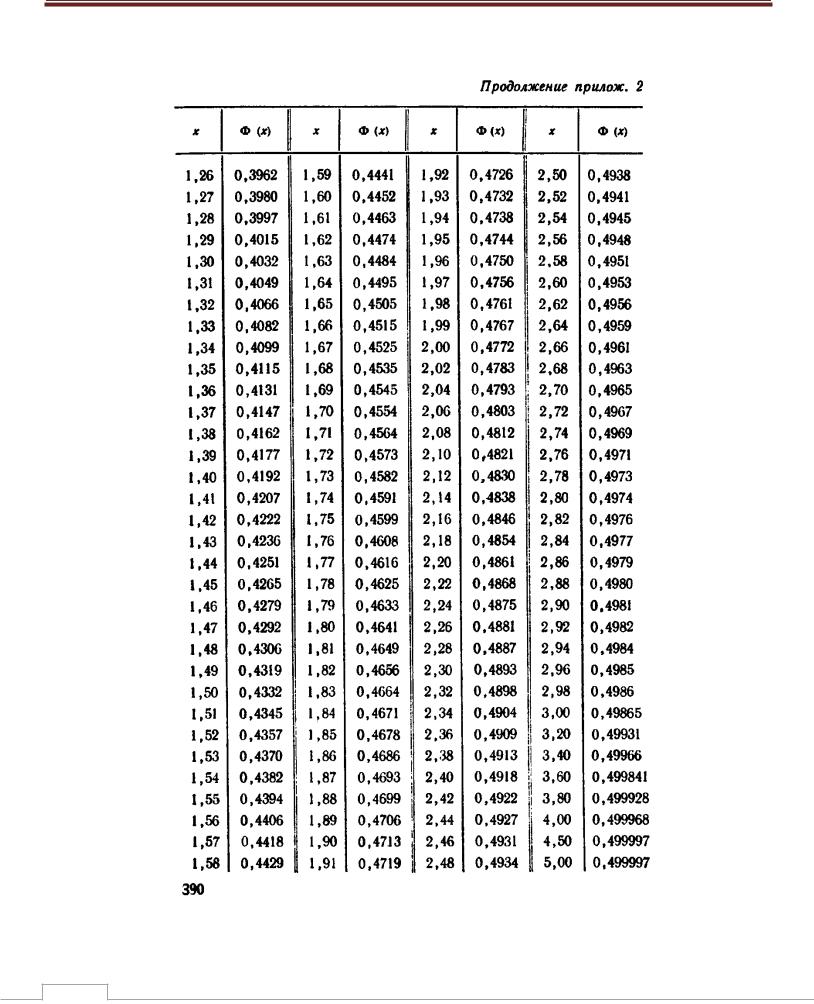
Функция Лапласа затабулирована. Для x 3 |
(x) 0.5 (с большой степенью точности). |
|||||||||||||||||||||||||||||||||||||||
Можно показать, что F (x) 0.5 (x) , и, следовательно, |
|
F (x) 0.5 ( |
x M |
) |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Функция Лапласа используется для вычисления вероятностей нормального распределения |
||||||||||||||||||||||||||||||||||||||||
P(a X b) F (b) F (a) 0.5 ( |
b M |
) (0.5 ( |
a M |
)) ( |
b M |
) ( |
a M |
) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, имеем формулы (вывести самостоятельно!) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
P(a X b) ( |
b M |
) ( |
a M |
) |
|
|
|
(1) |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P( X a) 0.5 ( |
a M |
) |
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
P( X b) ( |
b M |
) 0.5 |
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
P( |
|
X M |
|
) P(M X M ) 2 ( ) |
(4) |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 1. Случайная величина X распределена нормально с математическим ожиданием |
||||||||||||||||||||||||||||||||||||||||
M ( X ) 6, 4 |
и средним квадратическим отклонением ( X ) 2.7 . Найти вероятность того, что она |
|||||||||||||||||||||||||||||||||||||||
принимает значения: а) |
в интервале (4; 5); |
б) |
больше 2; в) |
меньше 7,2; |
г) либо меньше 3, либо |
|||||||||||||||||||||||||||||||||||
больше 9; |
д) отличающиеся от M ( X ) |
не более чем на 0,4. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
P(4 X 5) ( |
5 6.4 |
) ( |
|
4 6.4 |
) ( 0.52) ( 0.89) (0.52) (0.89) |
||||||||||||||||||||||||||||||||||
а) |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2.7 |
|
|
|
|
|
|
|
2.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0.1985 0.3133 0.115 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
б) |
P( X 2) 0.5 ( |
2 6.4 |
) 0.5 (1.63) 0.5 0.448 0.948 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3
Занятие 11-12
|
в) |
P( X 7.2) ( |
7.2 6.4 |
) 0.5 (0.30) 0.5 0.118 0.5 0.618 |
|||||
|
2.7 |
||||||||
|
|
|
|
|
|
|
|
||
|
P( X 3 X 9) 1 P(3 X 9) 1 ( ( |
9 6.4 |
) ( |
3 6.4 |
)) 1 (0.96) (1.26) |
||||
г) |
2.7 |
2.7 |
|||||||
|
|
|
|
|
|
||||
1 0.3315 0.3962 0.272
д) P( X 6.4 0.4) 2 ( 0.42.7) 2 (0.15) 2 0.0596 0.119
Пример 2. Случайная величина Х является нормально распределенной. Ее математическое ожидание равно 18, а вероятность ее попадания в интервал (16; 20) равна 0,98. Найти среднее квадратическое отклонение случайной величины.
Решение.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 18 |
|
|
|
16 18 |
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
||||||||||
|
|
P 16 X |
20 |
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
x |
|
x |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
Откуда |
|
|
0,49 .Найдем значение аргумента z |
функции Лапласа z |
. |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из таблицы ( см. приложение ) получаем z = 2,33. Значит x |
|
2 |
|
0,86 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2,33 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§6. Правило трех сигм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим формулу |
P( |
|
X M |
|
) 2 ( |
|
|
). |
Введем новую переменную t |
|
|
. |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
P( |
|
X M |
|
t) 2 (t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пусть t 3, |
тогда |
P( |
|
X M |
|
3 ) 2 (3) 0.9973 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввероятность того, что отклонение НСВ, имеющей нормальное распределение, от ее математического ожидания по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0.9973, т.е. практически равна единице.
4

Занятие 11-12
§7. Нормальное распределение как приближение биномиального.
Теорема. Если в биномиальном распределении n , то оно приближается к нормальному с параметрами M np и 
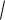 npq .
npq .
Замечание. При аппроксимации используют следующее правило: если концевая точка входит в промежуток, то ее включают вместе с отрезком длины 0.5; если концевая точка не входит в промежуток, то ее исключают вместе с отрезком длины 0.5.
Пример 5. Подбрасываем монету 20 раз. Найти вероятность того, что "орел" выпадет:
|
a) |
от 5 до 13 раз включительно; b) не менее 15 раз; c) ровно 7 раз; d) менее 8 раз. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Имеем: |
n 20 p q 0.5 |
|
M (X ) 20 0.5 10 |
|
|
20 0.5 0.5 5 |
|||||||||||||||||||||
а) |
P(5 X 13) ( |
13.5 |
|
10 |
) ( |
4.5 |
10 |
) (1.57) (2.46) 0.4418 0.4931 0.935 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
b) |
P( X 15) 0.5 ( |
14.5 |
|
10 |
) 0.5 (2.01) 0.5 0.4778 0.022 |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
5 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
c) |
P( X 7) P(6.5 X 7.5) ( |
7.5 |
|
10 |
) ( |
6.5 |
|
10 |
) (1.12) (1.57) 0.3686 0.4418 0.073 |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||
|
(P (7) C 7 0.520 0.074) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
20 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d) P( X 8) (7.5 10) 0.5 (1.12) 0.5 0.3686 0.5 0.131

 5
5
§8. Предельные теоремы теории вероятностей
Закон больших чисел.
Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт асимптотического приближения среднего значения большого числа опытных данных к математическому ожиданию случайной величины.
В основе доказательств этих теорем лежит неравенство, установленное известным русским математиком Чебышевым. Это неравенство можно получить на примере рассмотрения дискретной случайной величины, имеющей n возможных значений x1, x2 , , xn .
Дисперсия такой величины равна
|
|
|
n |
|
|
|
Dx xi M x 2 pi . |
|
|
|
|
|
i 1 |
|
Пусть – любое положительное число. Выбросим из суммы все члены, для которых |
||||
xi M x |
|
. В этом случае сумма уменьшится |
|
|
|
|
|
||
|
|
k |
M x 2 p j , где k < n. |
|
|
|
Dx x j |
|
|
|
|
j 1 |
|
x j M x 2 заменить на меньшее |
Если теперь в правой части неравенства (7.2) все значения |
||||
значение 2, то неравенство усилится
5

Занятие 11-12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx 2 p j . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В этом неравенстве pj – это вероятности таких значений xj, для которых |
|
x j M x |
|
, а вся |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сумма p j представляет собой вероятность того, что случайная величина |
|
|
X M x |
|
|
|
больше , т.е. |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
j 1 |
|
|
|
|
|
2 P |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
D |
x |
|
|
X M |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
X M |
x |
|
|
Dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Неравенство |
называется |
|
неравенством Чебышева. |
Это неравенство |
|
позволяет оценить |
|||||||||||||||||||||||
вероятность появления разностей |
|
X M x |
|
больших, |
чем . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Замечание. |
Если рассмотреть противоположное событие |
|
X M x |
|
, то вероятность такого |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
события будет
P X M x 1 Dx .2
Пафнутий Львович Чебышев (произносится как «Чебышѐв) (4 (16 мая) 1821, Окатово, Калужская губерния — 26 ноября (8 декабря) 1894, Санкт-Петербург) — русский математик и механик.
Летом 1837 года Чебышев начинает изучение математики в Московском университете на втором физико-математическом отделении философского факультета. В 1838 году, участвуя в студенческом конкурсе, получил серебряную медаль за работу по нахождению корней уравнения n-ной степени. В 1847 году Чебышев утверждѐн в звании доцента и начинает читать лекции по алгебре и теории чисел в Петербургском университете. В 1850 году Чебышев защищает докторскую диссертацию и становится профессором Петербургского университета. Эту должность он занимал до старости. Чебышев скончался 8 декабря 1894 года за письменным столом. Погребѐн в родном имении, в селе Спас-Прогнанье (ныне Жуковского района Калужской области) у храма Преображения Господня, рядом с могилами родителей.
Чебышев считается одним из основоположников теории приближения функций. Работы также в теории чисел, теории вероятностей, механике. Из многочисленных открытий Чебышева надо упомянуть прежде всего работы по теории чисел. Начало их положено в прибавлениях к докторской диссертации Чебышева: «Теория сравнений», напечатанной в 1849 году. В 1850 году появился знаменитый «Mémoire sur les nombres premiers»,[2] где даны асимптотические оценки для суммы ряда по всем простым числам p. В 1867 году во II томе «Московского Математического Сборника» появился другой весьма замечательный мемуар Чебышева «О средних величинах», в котором дана теорема, лежащая в основе различных вопросов теории вероятностей и заключающая в себе знаменитую теорему Якова ернулли как частный случай.
Одним из любимых приѐмов Чебышѐва, которым он особенно часто пользовался, было приложение свойств алгебраических непрерывных дробей к различным вопросам анализа.
В течение сорока лет Чебышев принимал активное участие в работе военного артиллерийского ведомства и работал над усовершенствованием дальнобойности и точности артиллерийской стрельбы. В курсах баллистики до наших дней сохранилась формула Чебышева для вычисления дальности полета снаряда. Своими трудами Чебышев оказал большое влияние на развитие русской артиллерийской науки.
Теорема Чебышева. Пусть имеется конечная последовательность X1, X 2 , , X n независимых
случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной С
Тогда, каково бы ни было положительное число , вероятность события
6

Занятие 11-12
X1 X 2 X n m n
стремится к единице при n .
Доказательство. Положим
Sn X1 X 2 X n . n
Эта величина является случайным числом. Найдем ее математическое ожидание и дисперсию
|
1 |
|
n |
|
|
nm |
|
|
|
|||
M Sn |
|
M X i |
|
m . |
||||||||
|
n |
n |
||||||||||
|
|
|
i 1 |
|
|
|
|
|
||||
Так как X1, X 2 , , X n независимы, |
|
то дисперсия суммы случайных величин равна сумме |
||||||||||
дисперсий слагаемых |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
nC |
|
|
C |
|
||||
D Sn |
D X i |
|
|
|
. |
|||||||
2 |
2 |
|
||||||||||
|
n |
|
i 1 |
|
|
n |
|
n |
||||
Из неравенства Чебышева с учетом сделанных обозначений
P Sn M Sn 1 D Sn
2
получаем
P Sn m 1 nC 2 .
Следовательно, с ростом n вероятность события Sn m стремится к единице.
Суть теоремы Чебышева состоит в том, что она устанавливает связь между теорией вероятностей, которая рассматривает средние характеристики всего множества значений случайной величины, и математической статистикой, оперирующей с ограниченным множеством значений этой величины. Она показывает, что при достаточно большом числе измерений некоторой случайной величины среднее арифметическое этих измерений приближается к математическому ожиданию.
Центральная предельная теорема.
Многие непрерывные случайные величины имеют нормальное распределение. Это обстоятельство во многом определяется тем, что суммирование большого числа случайных величин с самыми разными законами распределения приводит к нормальному распределению этой суммы.
Указанное свойство подтверждается доказанной русским математиком |
Ляпуновым |
интегральной предельной теоремой. Приведем эту теорему без доказательства. |
|
Теорема. Если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Центральная предельная теорема имеет огромное значение для практики.
Представим себе, что определяется некоторый экономический показатель, например, потребление электроэнергии в городе за год. Величина суммарного потребления складывается из потреблений энергии отдельными потребителями, которые имеют случайные значения с разными распределениями. Теорема утверждает, что в этом случае, какое бы распределение не имели отдельные составляющие, результирующее потребление будет близко к нормальному.
Однако следует иметь в виду, что усиление влияния отдельных факторов может приводить к появлению отклонений от нормального распределения результирующего параметра, к возникновению,
например, |
асимметрии или эксцесса. Поэтому большое значение на практике уделяется |
|
экспериментальной проверке выдвинутых |
гипотез, в том числе и гипотезы о нормальном |
|
распределении. |
|
|
Задачи.
7

Занятие 11-12
1.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значения: а) в интервале от 12 до 14; б) больше 14; в) меньше 10; г) отличающиеся от М ( Х ) не более чем на 0.5.
2.Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного менее 0,7. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 0,4 мм, найти, сколько в среднем будет годных шариков из 100 изготовленных.
|
|
|
|
0, 7 |
|
2Ф 1, 75 2 0, 4599 |
|
М ( X ) 0, P( |
X |
|
0.7) 2Ф |
|
|
0,92 |
|
|
|
||||||
|
|
|
|
0, 4 |
|
|
|
|
|
|
|
Значит, из 100 шариков 92 будут годными.
3. Вероятность попадания стрелком в мишень равна 23 . Стрелком сделано 15 выстрелов.
Случайная величина Х – число попаданий в мишень. Найти вероятность того, что стрелок попадет: а) от 5 до 10 раз включительно; б) ровно 8 раз; в) более 13 раз; г) не менее 4 раз.
Решение задач.
3.30. Имеется случайная величина X, распределенная по нормальному закону, математическое ожидание которой равно 20, среднее квадратическое отклонение равно 3. Найти симметричный
относительно математического ожидания интервал, в который с вероятностью р = 0,9972 попадет случайная величина.
Р е ш |
е н и е . Так как P |
|
x M x |
|
2Ф x p 0,9972 , то |
|
||||
|
|
|
||||||||
Ф x p / 2 0,4986 .Соответствующее значению функции |
Ф z 0,4986 значение аргумента |
|||||||||
z x |
находим |
по таблице |
функции |
Лапласа |
z = 2,98. |
Учитывая, что |
||||
z x (x M x ) |
x 2,98 , |
находим |
x M x 2,98 x |
2,98 3 8,94 ; |
||||||
x M x 8,94 20 8,94 . |
|
|
|
|
|
|
||||
Искомый интервал будет иметь вид (11,06; 28,94).
3.31.Случайная величина X распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратическим отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,954 попадет случайная величина.
3.32.Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратическое отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадает с вероятностью 0,98.
3.33.Математическое ожидание нормально распределенной случайной величины количества сыра, используемого для изготовления 100 бутербродов, равно 1 кг. Известно, что с вероятностью 0,96 расход сыра на изготовление 100 бутербродов составляет от 900 до 1100г. Определить среднее квадратическое отклонение расхода сыра на 100 бутербродов.
3.34.При измерении нормально распределенной случайной величины оказалось, что ее среднее квадратическое отклонение равно 10, а вероятность попадания этой величины в интервал от 100 до 140, симметричный относительно математического ожидания, равна 0,86. Найти математическое ожидание этой величины и вероятность попадания ее в интервал от 90 до 150.
|
|
|
|
|
|
Ответы. |
|
|
|
|
|
|
3.30 f (x) |
1 |
|
e (x 5) |
2 |
18 3.31 (11; 19).3.32.(68,35;91,65).3.33. |
|
|
= 48,8 г.3.34. M |
|
120 |
Р =0,9973. |
|
|
|
|
|
x |
x |
|||||||
|
|
|
|
|||||||||
3 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
+Сборник Гмурмана 329-343.
омашнее задание по Кремеру № 4.20, 4.22, 4.23, 4.27, 4.28, 4.30.
8
Занятие 11-12
9
Занятие 11-12
10
