3. Характеристика закономерностей рядов распределения.

Наиболее полной информацией о разбросе данных в статистике считается знание закона распределения. Это ‑ закономерные изменения частот в зависимости от изменения варьирующего признака. Это наиболее обобщенная характеристика вариации. Кривая распределения – это графическое изображение линии, когда по оси абсцисс откладываются варианты, по оси ординат – частоты или частости, т.е. это непрерывная линия изменения частот в вариационном ряду.

Кривая распределения может быть эмпирической (опытной) и теоретической (когда выражена общая закономерность распределения в чистом виде, без влияния случайных факторов).

Нормальное распределение – наиболее часто используется в статистике. Распределение называется нормальным, если признак есть результат воздействия многочисленных и разнообразных факторов, не связанных друг с другом, и влияние каждого из них мало по сравнению с общим влиянием всех факторов. Аналитическая форма нормального распределения:

или

- ордината нормальной кривой (частости), t – нормированное отклонение , - с.к.о., е = 2,71,

Таким образом, кривая нормального распределения определяется 2 факторами: с/а и с.к.о.

Особенности кривой нормального распределения:

1. Колоколообразный характер

2. Симметричность относительно

3. Ассимптотическое приближение к оси x

4. C/а, мода и медиана совпадают

5. Имеет две точки перегиба t1

6. В пределах заключено 68,3% всех членов распределения; ‑ 95,4%; ‑ 99,7%.

Правило ‑ при нормальном законе распределения разброс, колеблемость

индивидуальных значений признака находится в диапазоне . Примеры нормального распределения: отклонение размеров деталей от номинала, распределение населения по размеру носимой обуви, по росту, весу и т.д.

Другие виды распределений: биноминальное распределение – при повторении одного испытания в неизменных условиях (выборочный контроль качества продукции).

- вероятность того, что x раз повторится событие А в n-испытаниях.

, где р – доля события А.

При малых n:

Гипергеометрическое распределение – задача типа: в партии N деталей, М ‑ забраковано. Производится случайная выборка в n штук. Чему равна вероятность, что в выборке m бракованных:

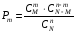, где m – число появлений признака (брака)

n – число испытаний, N – число единиц совокупности, M — из них забраковано

Распределение Пуассона ‑ применяется для анализа маловероятных событий

(задачи массового обслуживания)

где ‑ среднее число появления событий в одинаковых независимых испытаниях, x – частота данного события.

Необходимо отметить, что в статистике действует закон малых чисел: маловероятные события лучше подчиняются законам распределения, чем события достаточно вероятные. Эмпирические распределения, как правило, отличны от предполагаемых теоретических распределений. Для проверки их близости существуют специальные критерии согласия:

‑ критерий хи - квадрат –

где f_Э— эмпирические частоты, f_т – теоретические частоты, - находится для каждого варианта. По величине по таблице находят вероятность совпадения (существенности или несущественности расхождений)

Если P>0,5 – совпадение хорошее, 0,2<P<0,5 – совпадение удовлетво- рительное, P<0,2 – совпадение недостаточное.

Существуют и другие критерии согласия: Колмогорова, Ястремского, Романовского и др. Они изучаются в математической статистике.

Контрольные вопросы

1. Что такое вариация?

2. Какие показатели вариации Вы знаете?

3. Как исчислить размах вариации?

4. Что такое среднее абсолютное отклонение и как его исчислить?

5. Что такое среднеквадратическое отклонение и как его исчислить?

6. Что такое дисперсия?

7. Какие виды дисперсий применяются при анализе сгруппированных данных?

8. О чем говорит закон сложения дисперсий?

9. Что такое закономерности распределения? Что такое кривые распределения?

10. Охарактеризуйте нормальное распределение и его свойства?