
Российский государственный геологоразведочный университет
Кафедра механики
Сопротивление материалов
Напряженное состояние материала в точке
Учебно-методическое пособие и контрольные задания для студентов дневного и заочного отделений геологоразведочного, гидрогеологического и геофизического факультетов РГГРУ
Москва, 2008 г.
Составители: г.В. Лукошков, е.С. Булгаков, в.А. Барашков, о.В. Бадулин.
Сопротивление материалов. Напряженное состояние материала в точке.
Учебно-методическое пособие и контрольные задания для студентов дневного и заочного отделений геологоразведочного, гидрогеологического и геофизического факультетов РГГРУ.
В работе рассмотрены аналитические и графические способы исследования напряжений в наклонных сечениях при растяжении (сжатии) для линейного и плоского напряженных состояний. Методы определения главных напряжений и положение главных площадок при плоском напряженном состоянии.
Разработаны варианты заданий по исследованию линейного и плоского напряженного состояния материала в точке.
Введение.
Предлагаемое учебно-методическое пособие является руководством и пояснением к выполнению расчетно-графической работы по курсу «Сопротивление материалов» для студентов очного и заочного отделений геологоразведочного, гидрогеологического и геофизического факультетов РГГРУ.
Выполнение данной работы позволяет закрепить полученные теоретические знания и практические навыки решения задач по сопротивлению материалов.
Расчетно-графическая работа состоит из трех основных частей и охватывает основные типы задач по определению напряжений материала в точке при линейном и плоском напряженных состояниях.
-
Основы теории.
1.1. Понятие о напряженном состоянии
Величина и направление вектора напряжения в точке зависят от того, как ориентирована проведенная плоскость сечения.
Возьмем упругое тело, на которое действуют нагрузки, и через точку А проведем ряд плоскостей сечения, тогда в каждом сечении в точке А будут действовать напряжения σ1, σ2,…, σn (рис. 1).
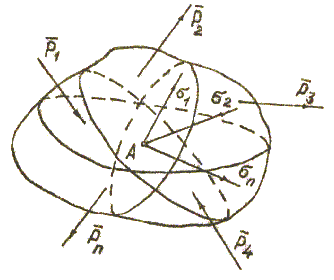
рис. 1
Через точку А можно провести бесчисленное множество плоскостей сечений, и в каждом из них будет действовать напряжение. Совокупность напряжений, действующих в данной точке во всех сечениях, проведенных через нее, называется напряженным состоянием в этой точке.
Для удобства изучения напряженного состояния в области этой точки проводят элементарный параллелепипед, грани которого стремятся к нулю, т.е. этот параллелепипед все время сжимается и стремится обратиться в рассматриваемую точку. На гранях этого параллелепипеда будут действовать напряжения в зависимости от того, как расположен параллелепипед. На его гранях могут действовать либо только нормальные напряжения, либо только тангенциальные напряжения, или, наконец, те и другие напряжения.
Возьмем элементарный параллелепипед в области точки А и так его сориентируем, чтобы на его гранях действовали только нормальные напряжения (рис. 2).
 рис.
2
рис.
2
Условимся называть его грани главными сечениями, а нормальные напряжения, действующие на главных площадках – главными напряжениями.
Таким образом, будем иметь три пары главных площадок и три главных напряжения σ1, σ2 и σ3. Такое напряженное состояние, когда действуют три главных напряжения, называется объемным или трехосным.
Однако может быть такой случай, когда одно из главных напряжений обратится в нуль (σ3 = 0), тогда будут действовать только два главных напряжения σ1 и σ2. Такое напряженное состояние называется плоским или двухосным (рис. 3).
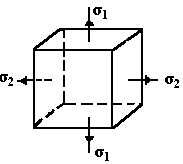 рис.
3
рис.
3
Возможен и еще более простой случай, когда будем иметь только одно главное напряжение σ1, остальные два σ2 и σ3 обратятся в нуль, такое напряженное состояние называется линейным (рис. 4).
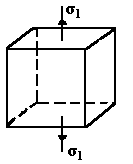 рис.
4
рис.
4
Лучшим примером линейного напряженного состояния является простое растяжение или сжатие.
Нумерация главных напряжений производится не произвольно, а по следующему правилу. За первое главное напряжение (σ1), принимают наибольшее по алгебраической величине, а за третье (σ3) – наименьшее по алгебраической величине.
1.2. Линейное напряженное состояние
а) АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ
Возьмем брус, который подвергается растяжению, найдем напряжения в наклонном сечении под углом α к поперечному сечению (рис. 5).
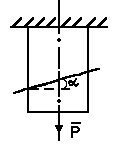 рис.
5
рис.
5
Для этого проведем наклонное сечение, отбросим верхнюю часть бруса и приложим внутренние силы, которые должны уравновесить нагрузку Р (рис. 6).
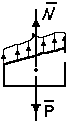 рис.
6
рис.
6
Все внутренние силы приведутся
к одной равнодействующей силе N,
направленной в противоположную нагрузке
Р сторону. Причем
![]() N, где Fα
– площадь наклонного сечения; р*
- полное напряжение в наклонном
сечении.
N, где Fα
– площадь наклонного сечения; р*
- полное напряжение в наклонном
сечении.
Так как
![]() (где F – площадь
поперечного сечения), то можем записать
(где F – площадь
поперечного сечения), то можем записать
![]() ,
но
,
но
![]() (σ – напряжение в поперечном сечении),
отсюда
(σ – напряжение в поперечном сечении),
отсюда
![]() [1]
[1]
Построив вектор полного напряжения р* и разложив его вдоль внешней нормали к сечению и касательной к нему, получим нормальное напряжение в наклонном сечении σα и тангенциальное τα (рис. 7).
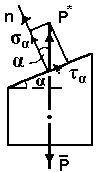 рис. 7
рис. 7
Если угол α получается поворотом внешней нормали против часовой стрелки, его считают положительным, в противном случае он будет отрицательным.
Определим σα и τα :
![]() ;
; ![]()
Подставив в эти выражения значение р* из формулы [1], получим:
![]()
![]() [2]
[2]
Исследуя полученные выражения, найдем экстремальные значения σα и τα :
при α=0 σα max= σ cos200, т.е. σα max = σ,
Наибольшие нормальные напряжения действуют в поперечных сечениях;
при α=900 σα min= σ cos2900, т.е. σα min = 0,
Наименьшее значение, равное нулю, нормальные напряжения имеют в продольном сечении;
при α=450 ![]() ,
т.е.
,
т.е.
![]() ,
,
Наибольшее тангенциальное напряжение действует в наклонном сечении под углом 450;
при α=0 ![]() ,
т.е.
,
т.е.
![]()
В поперечном сечении (α=0) тангенциальное напряжение отсутствует. А нормальные напряжения = σαmax. Это сечение является главным. Главное напряжение имеет максимальное значение. Во всех других сечениях нормальные напряжения будут меньше, чем в главном.
Условимся нормальное напряжение считать положительным, если направление его вектора совпадает с направлением внешней нормали – это растягивающее напряжение, в противном случае будем считать нормальное напряжение отрицательным – сжимающее напряжение.
Тангенциальное напряжение считают положительным, когда его вектор получается поворотом внешней нормали по направлению движения часовой стрелки, в противном случае оно будет отрицательным.
б) ГРАФИЧЕСКОЕ РЕШЕНИЕ (построение круга Мора)
Известно главное напряжение σ1, равное напряжению в поперечном сечении при растяжении. Нужно определить напряжения в этой точке в наклонном сечении под углом α. Решить эту задачу надо графически.
Проводим оси координат. По оси абсцисс откладываем нормальные напряжения, а по оси ординат тангенциальные (рис. 8).
 рис. 8
рис. 8
Отложим вдоль оси абсцисс значение главного напряжения σ в определенном масштабе. Получив отрезок ОА, разделим его пополам и из его середины (точка С) опишем окружность радиуса ОС=АС. Проведем из точки О луч под углом α с осью абсцисс до пересечения с окружностью (точка Дα). Для нахождения координат σα и τα соединим центр окружности с точкой Дα.
Из рис. 8 следует, что: ОКα=
ОС + СКα, но
![]() ,
а из треугольника ДαСКα
следует, что
,
а из треугольника ДαСКα
следует, что
![]() ,
но
,
но
![]() как
радиус круга, поэтому:
как
радиус круга, поэтому:
![]() .
.
Угол ДαСКα как внешний угол треугольника ОСДα равен сумме внутренних несмежных с ним углов, т.е. равен 2α.
Подставив
полученные значения отрезков ОС и
СКα в выражение для
ОКα , получим:
![]() или
или
![]()
Окончательно получим
![]() ,
а
,
а
![]()
Сравнив эти
выражения, замечаем, что абсцисса точки
в определенном масштабе равна нормальному
напряжению в наклонной площадке, т.е.
![]() .
.
Из треугольника
СДα Кα
следует, что Дα Кα
= CДα
sin2α, но
![]() ,
поэтому
,
поэтому
![]() ,
а
,
а
![]() .
.
Отсюда следует,
что ордината точки Дα в
определенном масштабе равна тангенциальному
напряжению в наклонной площадке, т.е.
![]() .
.
Таким образом, координаты точки Дα дают нам значения напряжений, действующих в наклонной площадке под углом α. При помощи построенного круга, называемого кругом напряжения, можно определить напряжения во всех сечениях, проведенных через рассматриваемую точку, т.е. круг определяет напряженное состояние в точке. Этот метод был предложен немецким исследователем Мором, и поэтому часто круг напряжений называют кругом Мора.
в) ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
Определим нормальные и касательные напряжения на двух взаимно перпендикулярных площадках.
Для площадки, наклоненной под углом α, по формуле [2] имеем:

Для взаимно
перпендикулярной площадки при значении
угла
![]() нормальные и касательные напряжения
можно определить или непосредственно
из условия равновесия верхней или нижней
части стержня (рис. 9), или по формулам
[2] с заменой α на
нормальные и касательные напряжения
можно определить или непосредственно
из условия равновесия верхней или нижней
части стержня (рис. 9), или по формулам
[2] с заменой α на
![]() .
.
Применяя формулы [2], получим:
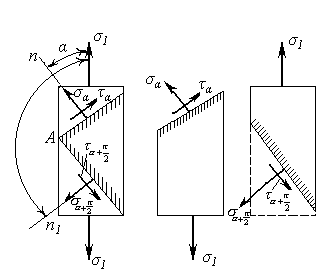 рис.
9
рис.
9
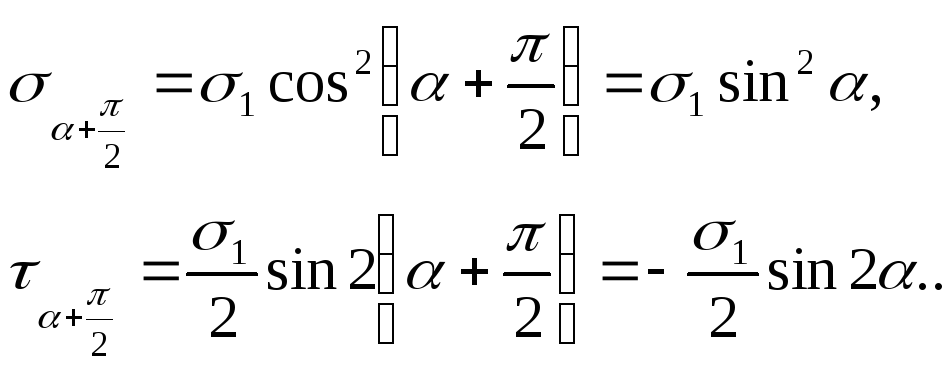
Анализируя полученные результаты, видим, что, во-первых,
![]()
т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам постоянна и равна главному напряжению; во-вторых,
![]()
т.е. на двух взаимно перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения (закон парности или взаимности касательных напряжений). При этом касательные напряжения на двух взаимно перпендикулярных площадках направлены оба либо к ребру пересечения площадок, либо от ребра, как на рис. 9.
Например, если
изменить знак σ, то напряжения
![]() и
и
![]() изменят свое направление на противоположное
и будут оба направлены к ребру А
пересечения площадок.
изменят свое направление на противоположное
и будут оба направлены к ребру А
пересечения площадок.
Закон парности (взаимности) касательных напряжений имеет силу не только для одноосного, но и для любого другого напряженного состояния: двухосного и объемного.
1.3. Напряжения в наклонных сечениях при растяжении (сжатии) по двум взаимно перпендикулярным направлениям
а) АНАЛИТИЧЕСКИЙ МЕТОД РЕШЕНИЯ
Рассмотрим более общий случай плоского (двухосного) напряженного состояния, когда отличны от нуля два главных напряжения σ1 и σ2 (рис. 10а).
 рис.
10
рис.
10
Как уже было отмечено ранее, индексы у обозначений главных напряжений ставятся так, что соблюдается неравенство σ1 > σ2, положительный угол α между направлением σ1 и нормалью к произвольной площадке будем отсчитывать против часовой стрелки.
Между направлением
напряжения σ2 и площадкой
угол равен
![]() .
.
Напряжения σα
и τα в
произвольном наклонном сечении можно
или определить из условий равновесия
трехгранной призмы АВС (рис. 10б), или
вычислить по формулам [2], суммируя
напряжения от действия σ1 с
напряжениями от действия σ2
(при замене угла α на угол
![]() ).
).
В результате
получим
![]() откуда
откуда
![]() [3]
[3]
Далее
![]() откуда
откуда
![]() [4]
[4]
Из формулы 4 видно, что максимальные касательные напряжения равны полуразности главных напряжений
![]() [5]
[5]
и имеют место в сечениях, наклоненных под одним и тем же углом к направлениям σ1 и σ2, т.е. при α=45˚. Это следует из условия, что τmax соответствует sin 2α=1.
Определив
касательные напряжения на площадке,
перпендикулярной к площадке АВ,
убедимся, что и для двухосного напряженного
состояния сохраняет свою силу закон
парности касательных напряжений. В этом
можно убедиться также по формуле [4],
определив по ней значения
![]() и
и
![]() .
.
Частные случаи
1-й случай. Рассмотрим напряженное состояние, при котором σ1= σ2= σ (рис. 10в).
в этом случае
на всех площадках, проходящих через
исследуемую точку, касательное напряжение
![]() равно нулю, а нормальное напряжение
имеет одно и то же значение σα
= σ (см. формулы [3] и [4]). Такое
напряженное состояние называется
равномерным двухосным растяжением
(или сжатием).
равно нулю, а нормальное напряжение
имеет одно и то же значение σα
= σ (см. формулы [3] и [4]). Такое
напряженное состояние называется
равномерным двухосным растяжением
(или сжатием).
2-й случай. Рассмотрим напряженное состояние, представленное на рис. 10г, характеризующееся главными напряжениями σ1= σ и σ3= - σ. При этом σ2= 0.
Определим напряжения в сечениях, одинаково наклоненных к направлениям σ1 и σ3, т.е. при α=45˚ и α=135˚ .
По формулам [3]
и [4] получим σα = 0;
![]() =±σ.
Такое напряженное состояние называется
чистым сдвигом.
=±σ.
Такое напряженное состояние называется
чистым сдвигом.
б) ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ
Пусть известны главные напряжения σ1 и σ2, требуется определить напряжения на площадке под углом α. Проведем координатные оси. По оси абсцисс отложим главные напряжения σ1 и σ2 (рис. 11), получим отрезки ОА и ОВ. Отрезок АВ разделим пополам, получим точку С. Точку С примем за центр круга, и опишем его радиусом СА = СВ.
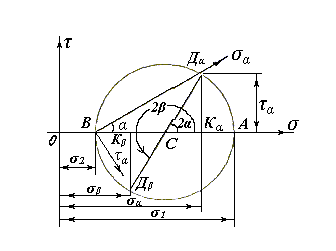 рис. 11
рис. 11
Из точки В проведем луч под заданным углом α к оси абсцисс до пересечения с кругом, найдем координаты точки пересечения луча с кругом Дα.
Из рис. 11 следует: ОКα = ОВ + ВС + СКα;
![]()
Подставив полученные значения отрезков ОВ, ВС и СКα в выражение для отрезка ОКα, получим:
![]()
После преобразований получим
![]()
Сравнив
приведенные выше выражения, приходим
к выводу, что абсцисса точки Дα
представляет нормальное напряжение
на наклонной площадке, т.е.
![]() .
.
Найдем ординату точки Дα . Из треугольника Дα СКα следует:
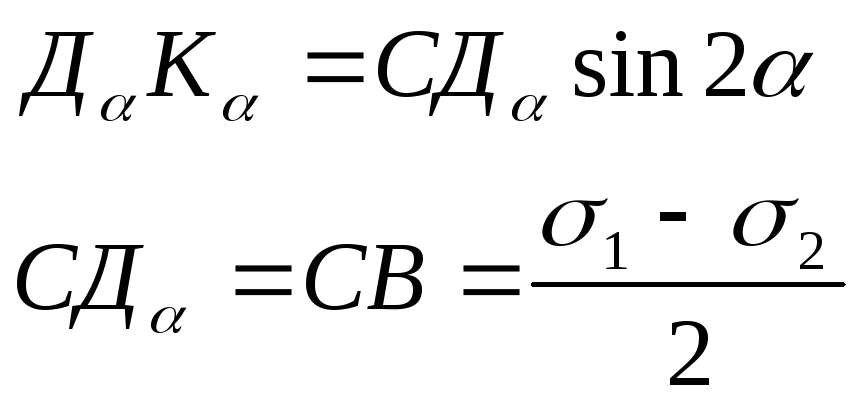
поэтому
![]()
так как
![]() ,
то
,
то
![]()
Таким образом,
ордината точки Дα выражает
тангенциальное напряжение на наклонной
площадке
![]() .
.
Для определения напряжений на перпендикулярной площадке к данной, строим двойной угол (2β=180˚+2α), путем продолжения радиуса СДα до пересечения с кругом получаем точку Дβ, координаты которой и есть напряжения на этой площадке.
Таким образом, координаты любой точки круга дают напряжения на наклонных площадках, т.е. круг определяет напряженное состояние в данной точке.
1.4. Определение главных напряжений и положения главных площадок при плоском напряженном состоянии
а) АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ
Данная задача обратна предыдущей. Теперь известны нормальные и касательные напряжения, действуя по граням элемента (рис. 12.а). требуется определить положение главных площадок (угол φ) и величину главных напряжений (σmax и σmin). Рассмотрим равновесие трехгранной призмы с основанием АВС (рис. 12.б). Примем, что σα>σβ. Угол φ будем отсчитывать от направления большего напряжения до нормали к площадке. За положительное направление отсчетов угла φ примем направление против часовой стрелки.
 рис.
12
рис.
12
Площадь наклонной грани обозначим через dF. Тогда площадь вертикальной грани будет dF sin φ, а горизонтальной - dF cos φ.
Проектируя все силы на направление σφ, получим
![]()
Проектируем теперь все силы на направления τφ
![]()
Сократив на dF и введя функции двойных углов, получим:
![]() [6]
[6]
![]() [7]
[7]
При изменении угла наклона площадки φ величина σφ будет непрерывно изменяться.
Чтобы отыскать
положения главных площадок, т.е. площадок,
на которых действуют экстремальные
нормальные напряжения, следует либо
приравнять нулю производную
![]() ,
либо приравнять нулю касательные
напряжения τφ, так как на
главных площадках касательных напряжений
нет.
,
либо приравнять нулю касательные
напряжения τφ, так как на
главных площадках касательных напряжений
нет.
В обоих случаях получаем следующую зависимость для определения угла φ0 наклона главных площадок:
![]()
или
![]() [8]
[8]
Для получения экстремальных значений нормальных напряжений, т.е. величин главных напряжений, значение угла из формулы [8] подставим в формулу [6]. Предварительно тригонометрические функции в формуле [6] следует выразить через тангенс двойного угла. Для этого используют известные формулы тригонометрии:
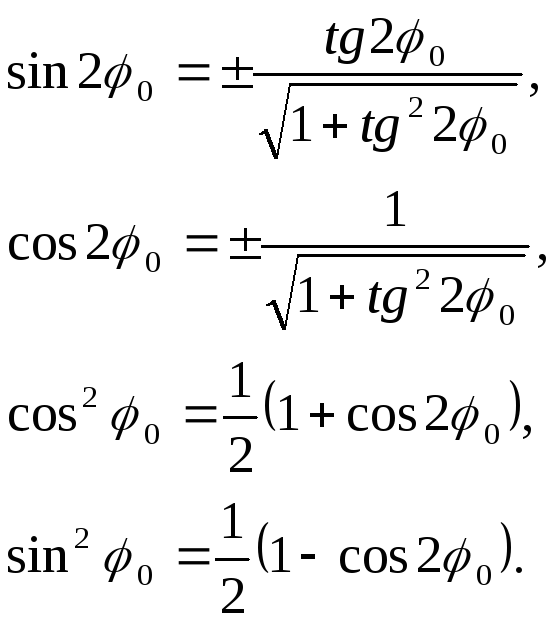
После несложных преобразований, которые необходимо сделать учащемуся самостоятельно, получим следующую формулу для определения величин главных напряжений
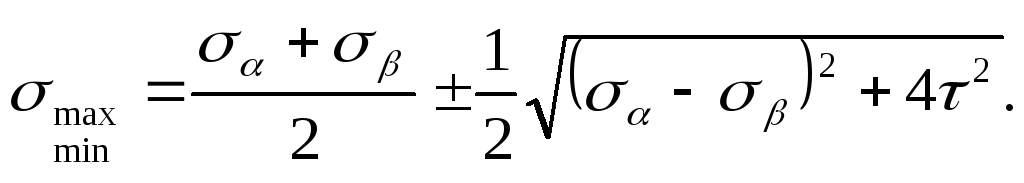 [9]
[9]
Если одно из заданных нормальных напряжений равно нулю, то формула [9] упростится и примет вид
 [10]
[10]
Этой формулой будем пользоваться в дальнейшем при изучении изгиба и сложного сопротивления.
Исследуя вторую
производную
![]() можно
убедиться, что на главной площадке под
углом φ0 при принятых
условиях (σα>σβ)
действует максимальное главное
напряжение, а на площадке под углом
φ0+90˚ действует
минимальное главное напряжение.
можно
убедиться, что на главной площадке под
углом φ0 при принятых
условиях (σα>σβ)
действует максимальное главное
напряжение, а на площадке под углом
φ0+90˚ действует
минимальное главное напряжение.
Пример. Определить величину и направление главных напряжений в случае напряженного состояния, показанного на рис. 13.1.
 рис.
13
рис.
13
Р е ш е н и е. По формуле [8] определяем положение главных площадок, перпендикулярных плоскости чертежа
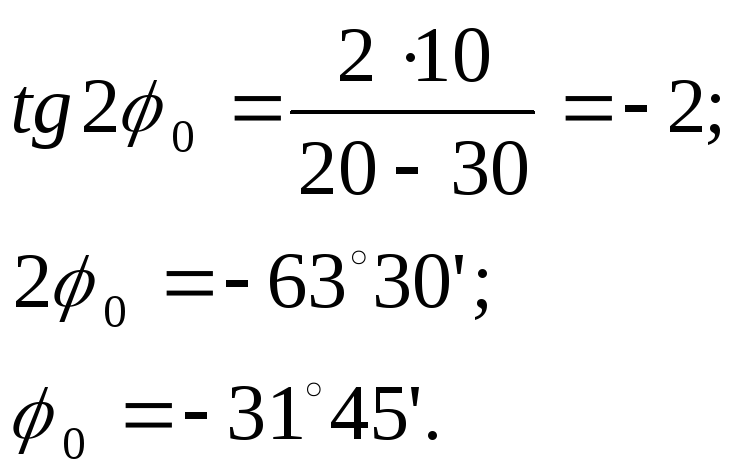
Знак «минус» показывает, что φ0 отсчитывается от направления σα=30 мПа по часовой стрелке.
По формуле [9] получим:

В соответствии со сказанным выше σmax действует на площадке под углом φ0, σmin – на площадке под углом φ0 + 90˚.
б) ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ ГРАФИЧЕСКИМ МЕТОДОМ
При известных σα, σβ и τα необходимо графически определить направление и величину σmax = σ1 и σmin = σ3. Графическое построение (рис. 14.1).
Принимаем масштаб напряжений. Проводим оси прямоугольной системы координат. Отложим на оси нормальных напряжений σα = OKα и σβ = OKβ. Восстанавливаем перпендикуляры к оси σ, отложив на них отрезки КαДα = τα и КβДβ = τβ (направление τα и τβ принимаются в зависимости от знаков напряжений). Соединив точки Дα и Дβ, получаем центр С круга Мора. Радиусом С Дα или С Дβ описываем окружность, пересечение которой с осью нормальных напряжений дает точку А и В. Тогда ОА=σ1 и ОВ= σ3. Чтобы получить направление 1-го и 2-го главных напряжений на круге Мора, необходимо воспользоваться полюсом М.
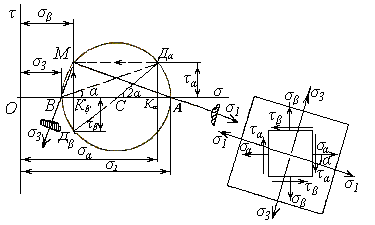 рис.
14
рис.
14
-
Зависимость между деформациями и напряжениями при плоском напряженном состоянии. Удельная работа деформации.
Пусть брус прямоугольного сечения (рис. 15) растягивается по двум взаимно перпендикулярным направлениям х и у напряжениями σ1 и σ2. Определим относительные удлинения, которые получит брус в направлениях осей х, у и z.
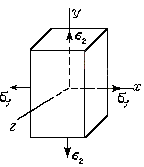 рис.
15
рис.
15
Если бы на брус
действовало одно растягивающее напряжение
σ1, то относительное
удлинение в направлении растяжения
согласно закону Гука было бы равно
![]() а
по осям у и z брус
получил бы относительные укорочения
а
по осям у и z брус
получил бы относительные укорочения
![]()
Аналогично
этому при действии только одного
растягивающего напряжения σ2
относительное удлинение в направлении
растяжения было бы равно
![]() а по осям х и z брус
получил бы относительные укорочения
а по осям х и z брус
получил бы относительные укорочения
![]()
Следовательно, при одновременном действии напряжений σ1 и σ2 относительные деформации в направлениях осей х, у и z будут соответственно равны:
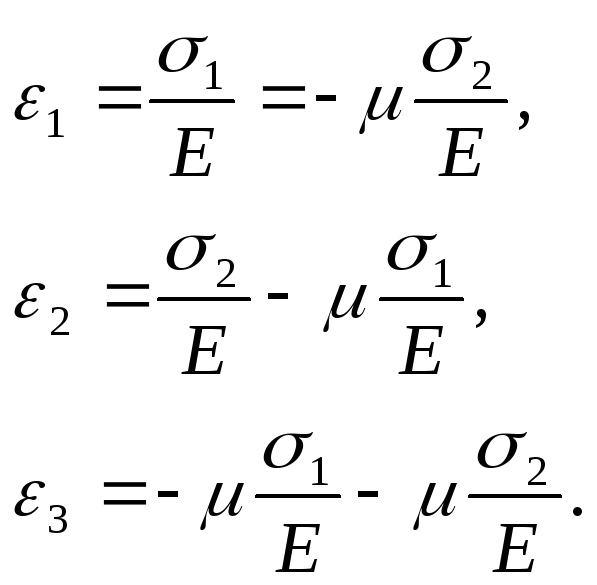
В общем случае объемного напряженного состояния относительные деформации ε1, ε2 и ε3 соответственно будут равны:
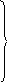
 [11]
[11]
Частные случаи. 1) Простое растяжение: σ1= σ, σ2= 0, σ3=0; тогда по формуле [11] получим:
![]()
2) Растяжение по двум взаимно перпендикулярным направлениям, если σ1= σ2= σ; σ3=0; тогда из формул [11] получим:

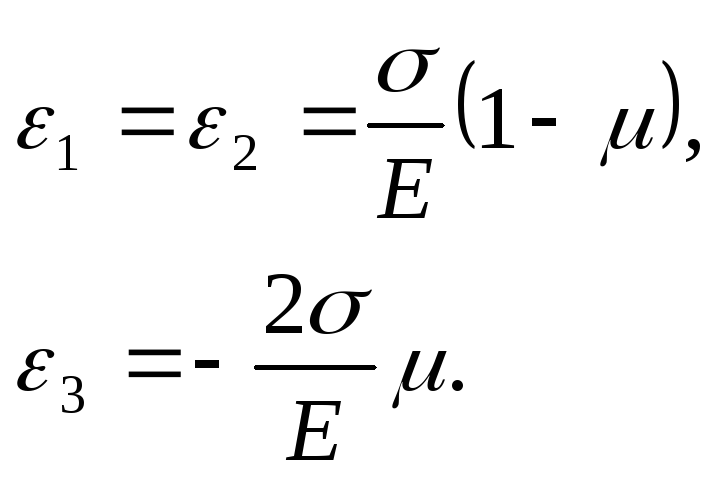
Е сли
напряженное состояние плоское, т.е.
σ3=0, и известны относительные
деформации ε1 и ε2,
то из формул [11] легко определяются
напряжения σ1 и σ2:
сли
напряженное состояние плоское, т.е.
σ3=0, и известны относительные
деформации ε1 и ε2,
то из формул [11] легко определяются
напряжения σ1 и σ2:
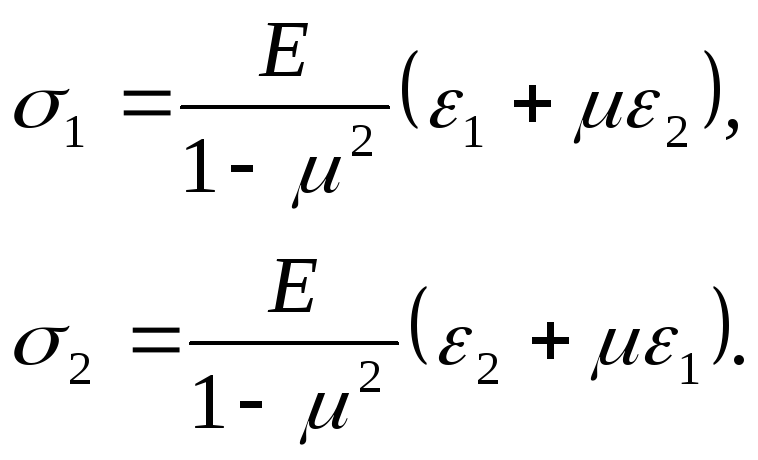
Этими формулами часто пользуются при экспериментальном определении напряжений, измеряя ε1 и ε2.
Найдем теперь выражение удельной работы деформации при растяжении или сжатии по двум направлениям. Удельная работа деформации при растяжении (сжатии) в одном направлении выражается формулой
![]() [12]
[12]
При плоском напряженном состоянии, ориентируя грани кубика со стороной, равной единице, по площадкам, где действуют напряжения σ1 и σ2, получим:
![]()
Подставив сюда значения ε1 и ε2 из формул [11], при σ3 = 0 будем иметь:
![]()
или
![]() [13]
[13]
Это и есть выражение удельной работы при плоском напряженном состоянии.
Пример. Определить относительные деформации бруса ε1 и ε2, если растягивающее напряжение σ1=60 МПа, а сжимающее σ2=- 75 МПа (рис. 16). Модуль упругости Е=2,2·105 МПа. Коэффициент Пуассона μ=0,3.
Решение. На основании формул [11] имеем:
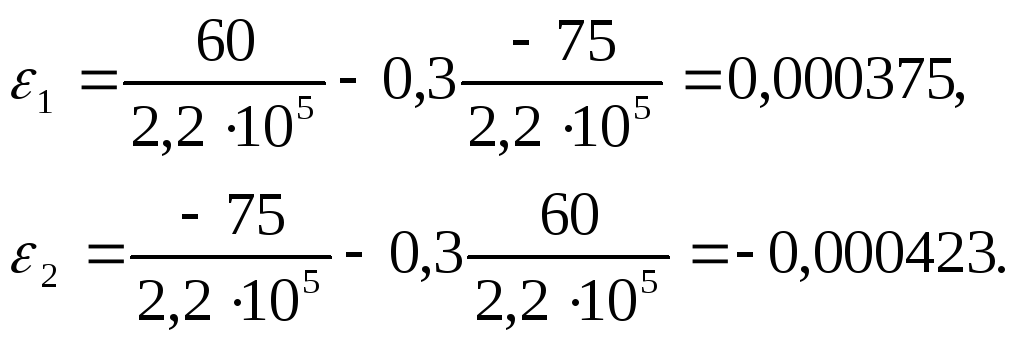
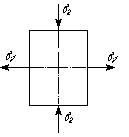 рис.
16
рис.
16
