Курс СТУ_Заочники_Никитин / КурсСТУ-8-Фильты на ОУ_Ник_130522

Ю.А. Никитин

Курс СТУ

Тема 8

Фильтры на ОУ

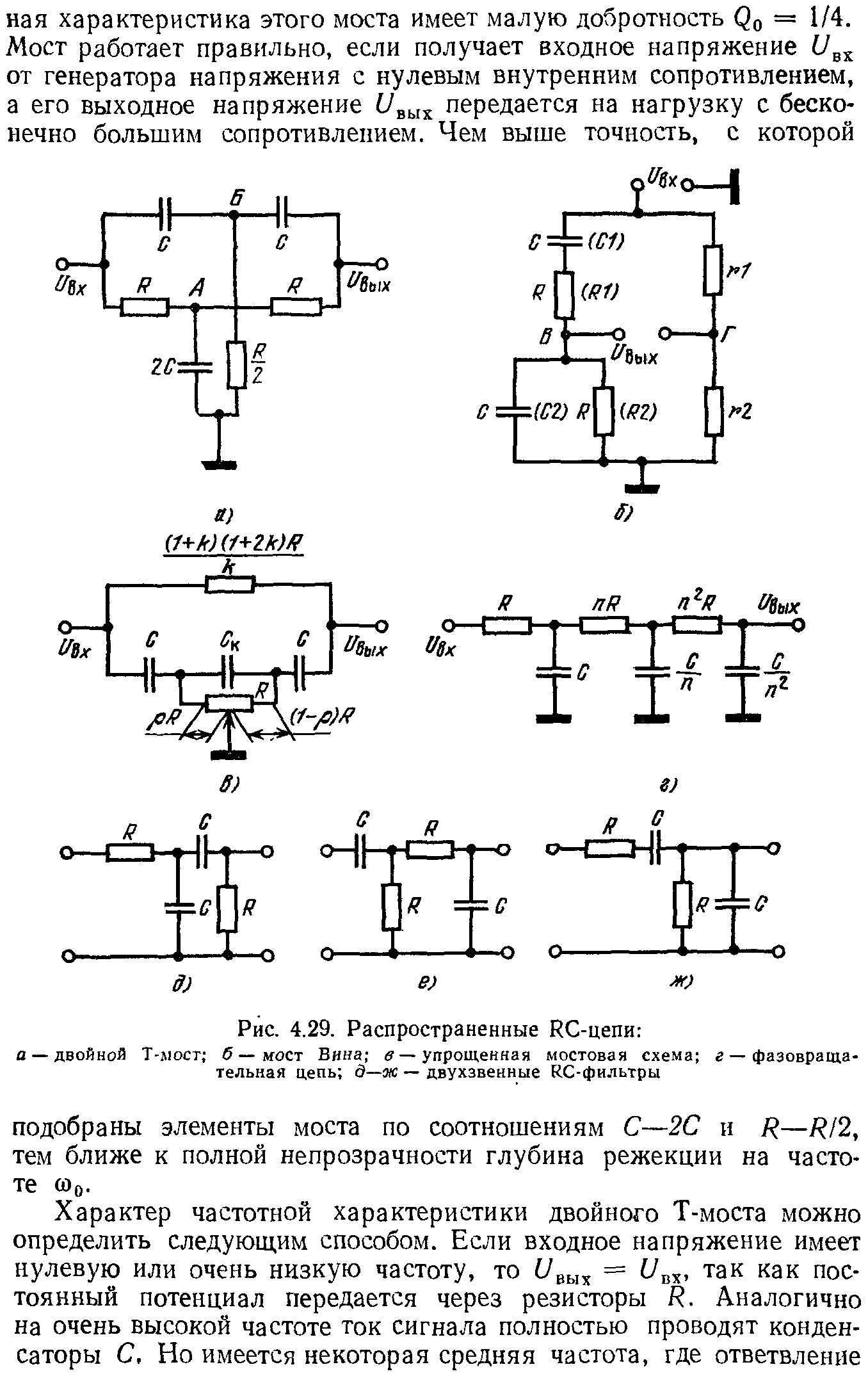
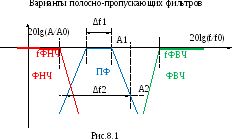
Фильтрами называют частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определенных полосах частот – рис.8.1. Фильтры можно классифицировать по их частотным характеристикам на полосно-пропускающие фильтры: фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ); на полосно-заграждающие фильтры: полосно-подавляющие фильтры ППФ); на режекторные фильтры; на фазовые фильтры.

Фильтры реализуют, в основном, на пассивных элементах L, R, C. В низкочастотном диапазоне индуктивные элементы имеют значительные массу и габариты, они нетехнологичны в производстве и ненадежны при эксплуатации, их параметры зависят от материала сердечника и его электрической стабильности в диапазоне эксплуатационных воздействий.

Активные аналоговые RC фильтры служат удачной альтернативой пассивным LC фильтрам в диапазоне до единиц мегагерц.

С помощью активных RC фильтров нельзя получить идеально-прямоугольную форму АЧХ (АЧХ вида «brick walls» – кирпичные стены), но можно обеспечить приемлемый компромисс между формой АЧХ и сложностью ее реализации. Во многих случаях требования к качеству фильтрации сигнала позволяют обойтись простыми фильтрами первого и второго порядка, а также каскадным включением таких фильтров.

Качество фильтра можно оценить с помощью «коэффициента прямоугольности» - параметра, который характеризуется отношением полос пропускания фильтра по определенным уровням – рис.8.1. В измерительной технике стандартные уровни A₁ минус 3дБ и A₂ минус 60дБ,

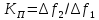, (8.1)

и

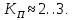
На рис.8.2 приведены возможные варианты формирования АЧХ усилителя на ОУ с помощью корректирующих звеньев первого порядка (RC звеньев). Изменяя сочетания типовых пассивных RC звеньев можно формировать желаемую амплитудно-частотную характеристику, после чего компенсировать потери с помощью буферного усилителя.

Отметим, что у RC фильтра первого порядка подъем/спад АЧХ происходит с наклоном ± 20дБ/дек = ± 6дБ/окт (рис.8.2) и в соответствии с (8.1) коэффициент K_П = 1000. Для получения K_П = 10 необходим RC фильтр третьего порядка, для K_П = 3 необходим RC фильтр шестого порядка, а для K_П = 2 необходим RC фильтр десятого порядка!

Активные RC фильтры принадлежат к классу линейных схем с сосредоточенными параметрами. В общем случае передаточную функцию линейной цепи n-го порядка можно описать следующим выражением:

, (8.2)

где A(s) – полином числителя;

B(s) – полином знаменателя;

a_і и b_і – вещественные коэффициенты;

n ≥ m.

Полиномы A(s) и B(s) можно разложить на элементарные множители первого и второго порядка с вещественными коэффициентами (раздел 3.5 Типовые звенья). Рассмотрим примеры реализации активных фильтров первого – второго порядка на типовых звеньях.

На рис.8.3 приведен вариант реализации полосно-подавляющего фильтра первого порядка (выход 2), и такого же фильтра, дополненного усилителем на ОУ (выход 9). На рис.8.4 приведены их ЛАХ и ЛФХ с учетом характеристик ОУ.

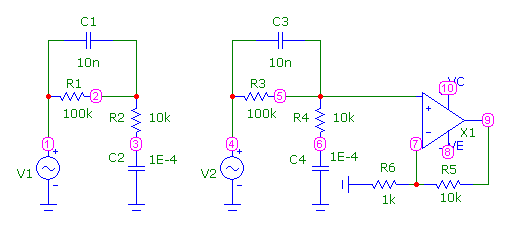
Рис.8.3

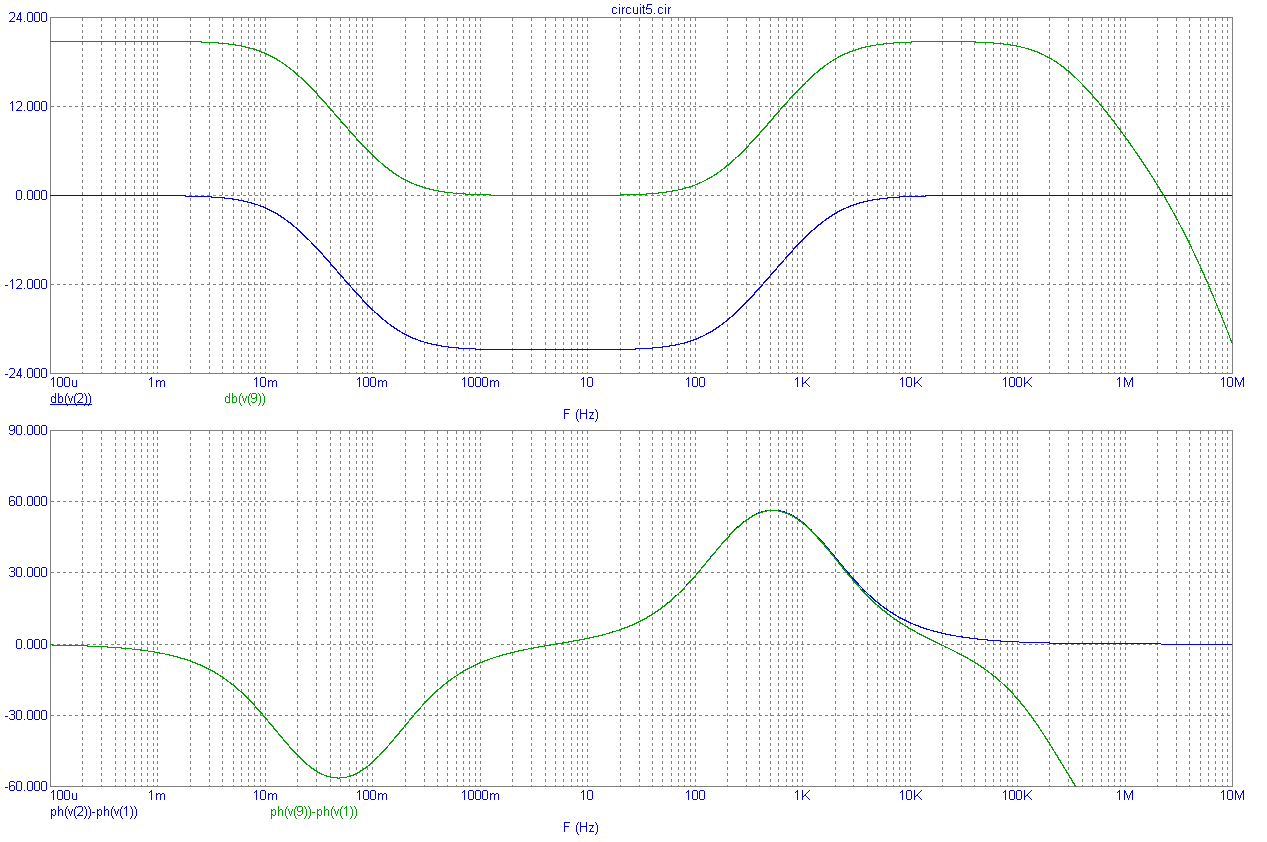
Рис.8.4

Возможно, однако, другое построение аналоговых активных фильтров – с помощью частотно-зависимых обратных связей. На рис.8.5 приведен вариант реализации пассивного полосового фильтра первого порядка (выход 18), и такого же фильтра выполненного на ОУ (выход 12). На рис.8.6 приведены их ЛАХ и ЛФХ.

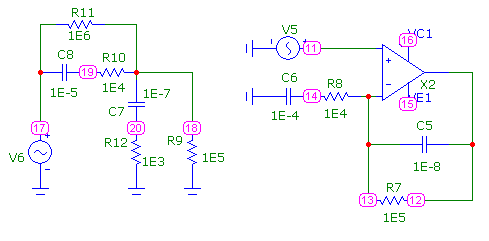
Рис.8.5

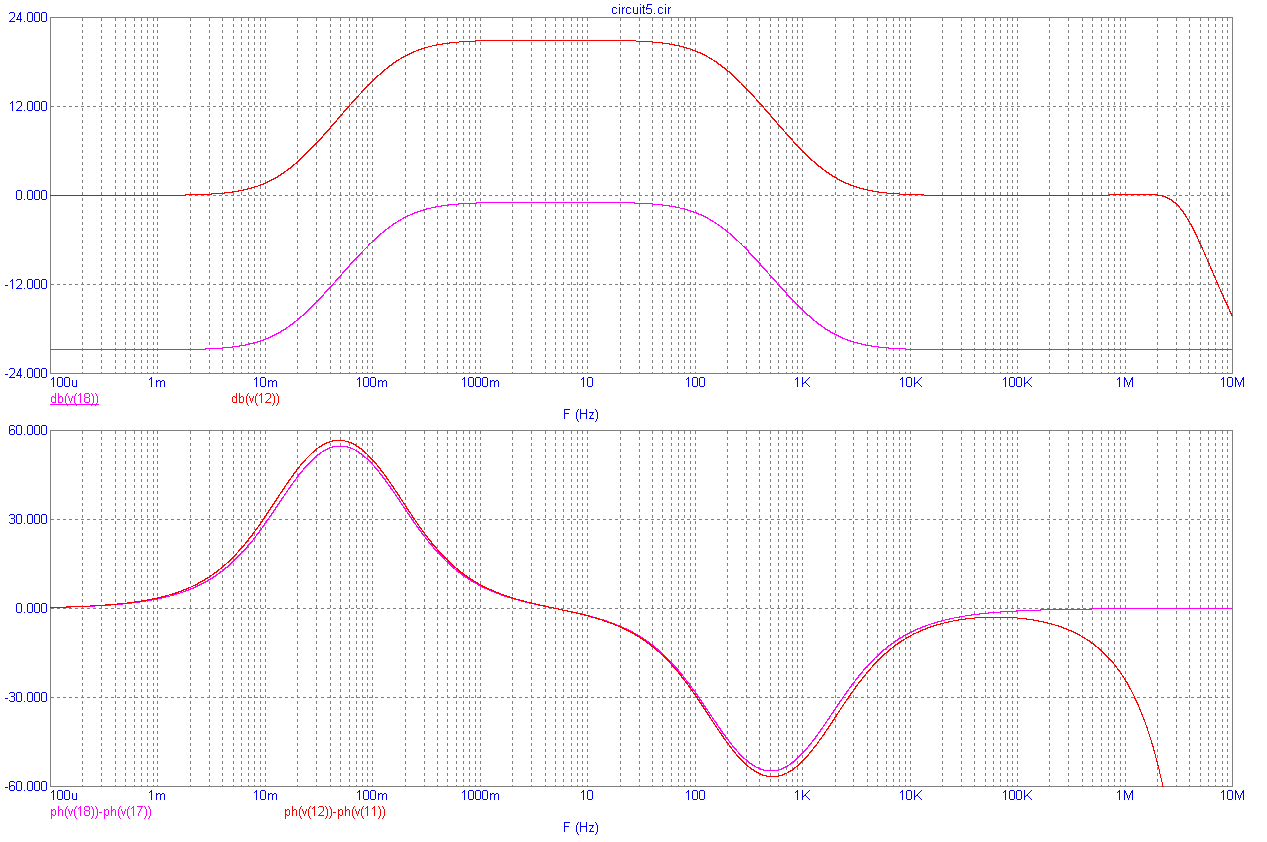
Рис.8.6

На рис.8.7 приведена схема активного ФНЧ первого порядка, а на рис.8.8 – его ЛАХ и ЛФХ.

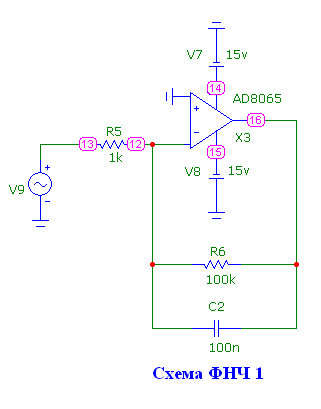
Рис.8.7

Рис.8.8

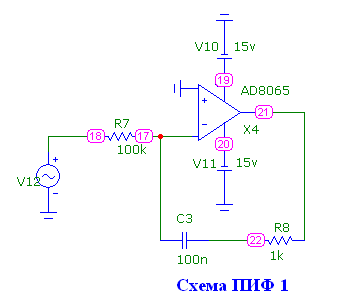
Рис.8.9

На рис.8.9 и рис.8.11 приведены примеры реализации звеньев пропорционально-интегрирующего фильтра (ПИФ), а на рис.8.10 и рис.8.12 – их ЛАХ и ЛФХ.

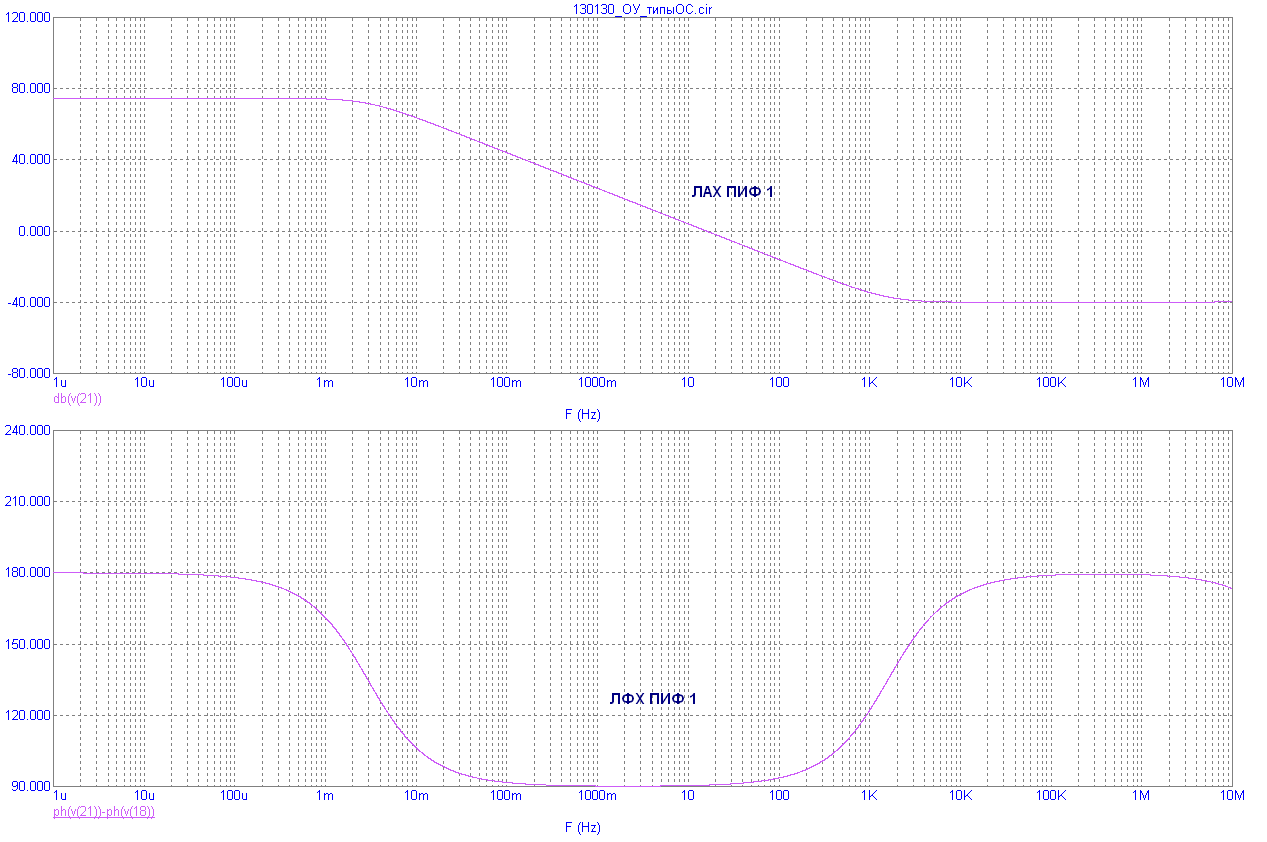
Рис.8.10

Рис.8.11

Рис.8.12

На рис.8.13 приведен пример реализации звена пропорционально-дифференцирующего фильтра (ПДФ), а на рис.8.14 – его ЛАХ, ЛФХ и реакция на периодическую импульсную последовательность с частотой следования 10Гц, 1кГц и 100кГц.

Рис.8.13

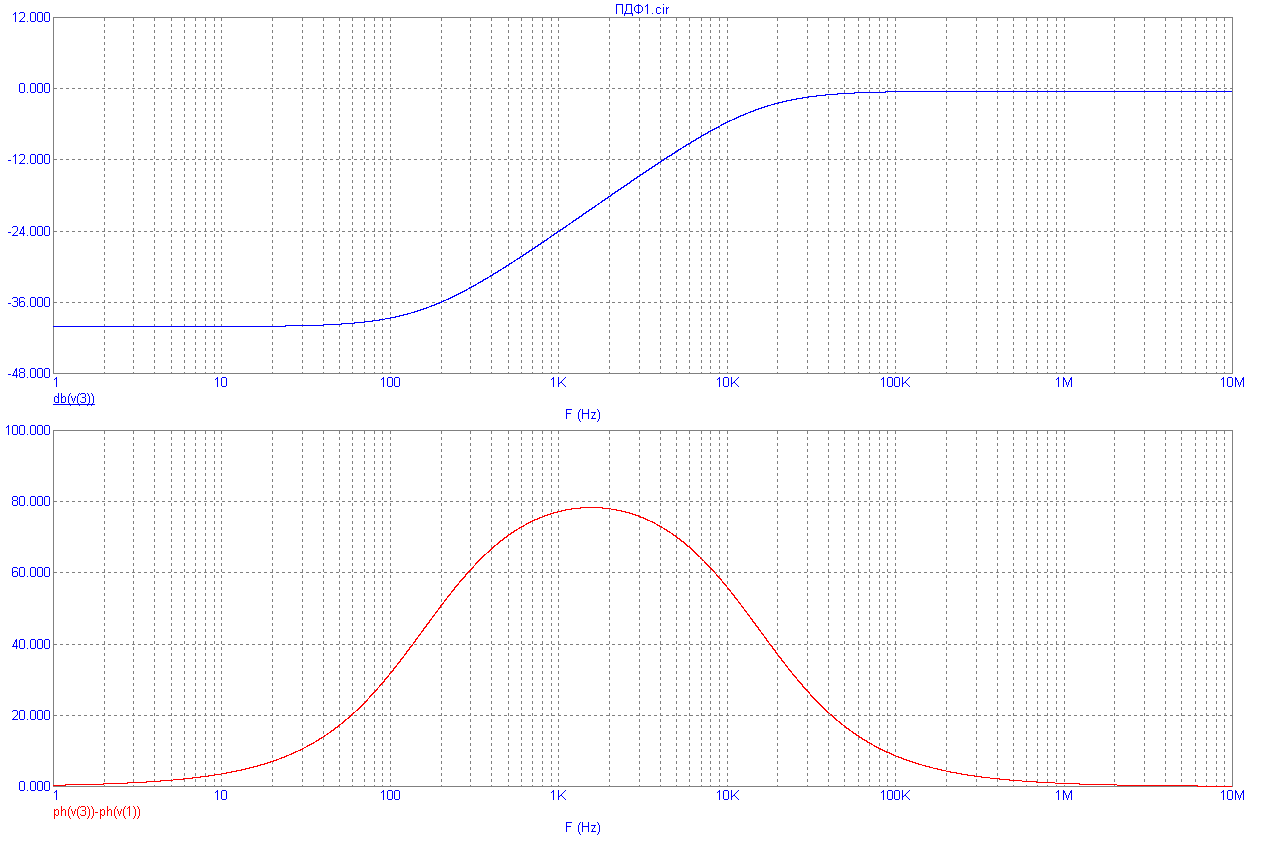
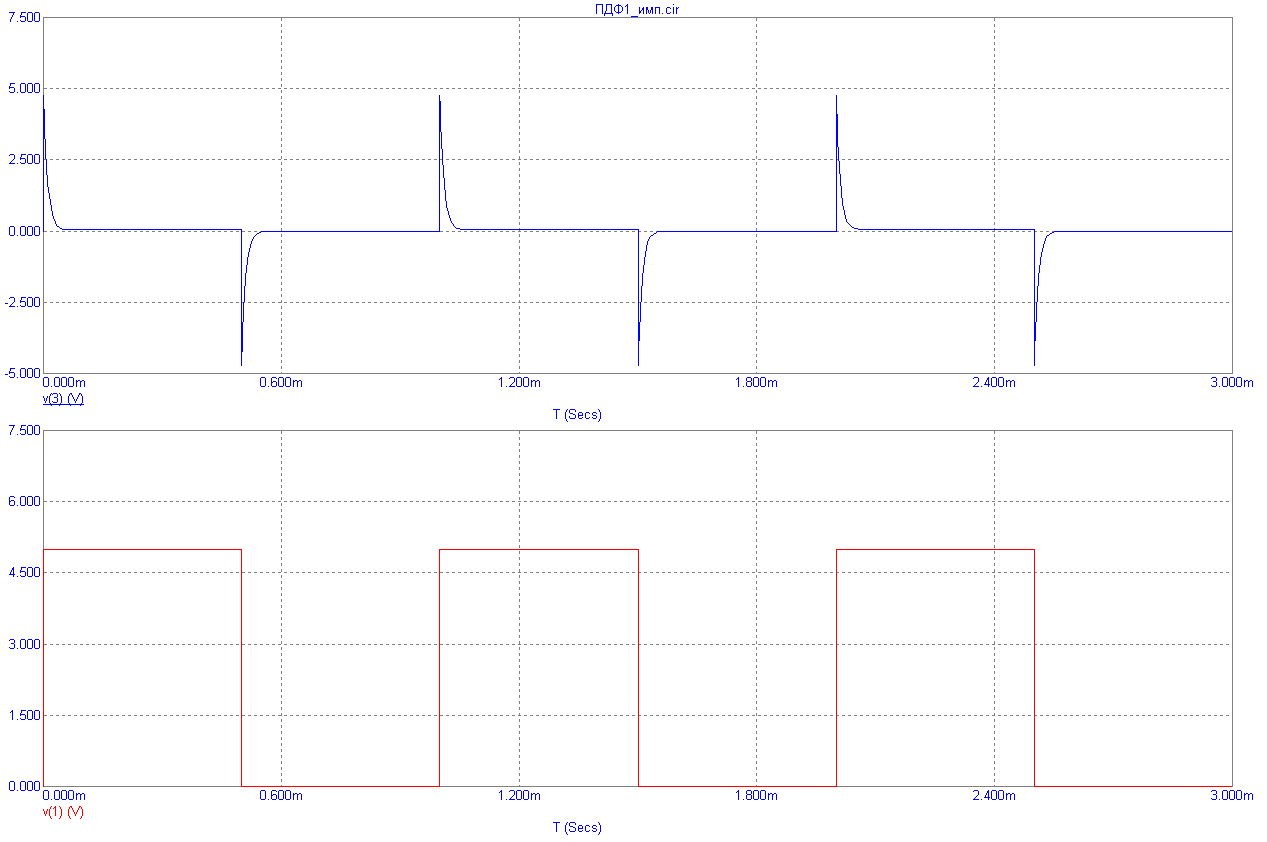
Рис.8.14

ФНЧ второго порядка (структура Саллена-Кея)

Электрическая схема фильтра приведена на рис.8.15, а его ЛАХ и ЛФХ на рис.8.16.

Передаточная функция ФНЧ имеет вид

(8.3)

его параметры

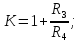
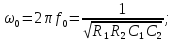
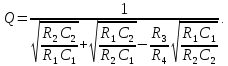
Рис.8.15

Рис.8.16

У этого фильтра высокое входное сопротивление, но невозможна независимая настройка всех параметров. Обычно настраивают f₀ и Q с помощью R₁ и R₂. При значениях Q > 10 схема становится чувствительной к изменению номинальных значений элементов, что нежелательно.

При построении фильтра Баттерворта второго порядка схему можно упростить, положив отсутствует. ЛАХ и ЛФХ фильтра Баттерворта второго порядка приведены на рис.8.17.

Рис.8.17

ФНЧ второго порядка (структура Рауха)

Передаточная функция ФНЧ (рис.8.18) имеет вид:

; (8.4)

его параметры

;

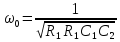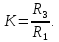
Рис.8.18

На рис. 8.19 приведена ЛАЧХ и ЛФХ этого фильтра, а также его реакция на импульсное воздействие – периодическую импульсную последовательность с частотой следования 1кГц, 10кГц и 100кГц.

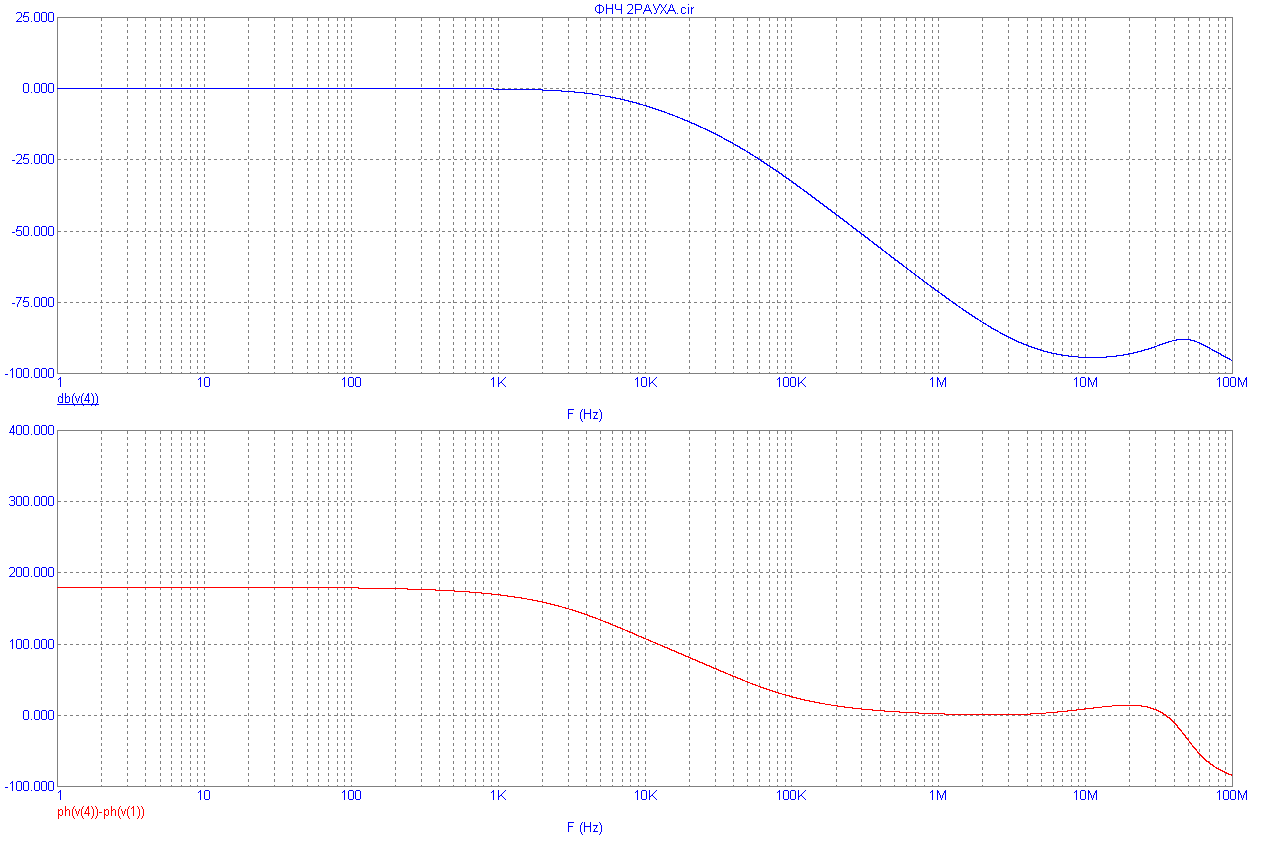
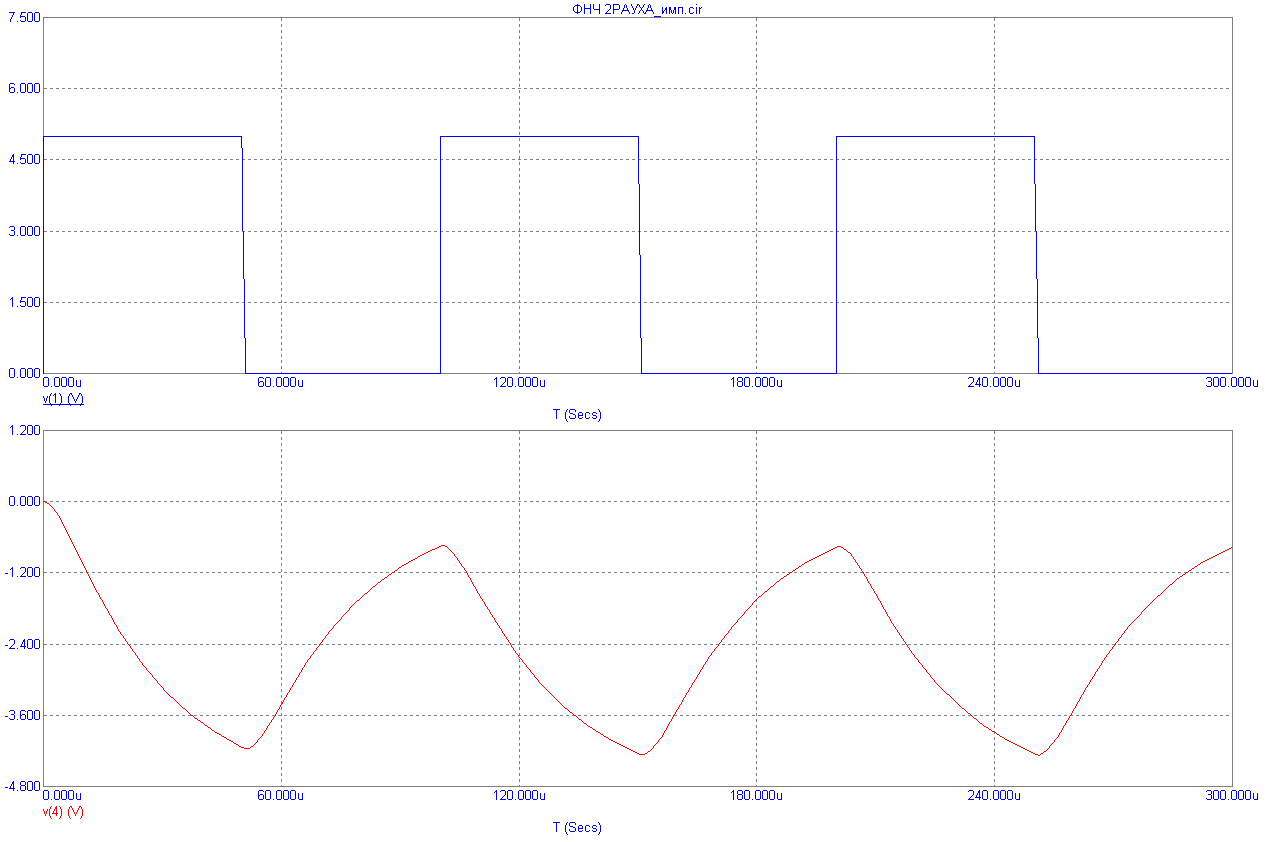
Рис.8.19

При изменении соотношения емкостей C₁/C₂ частотная характеристика изменяется, приобретая экстремум – рис. 8.20.

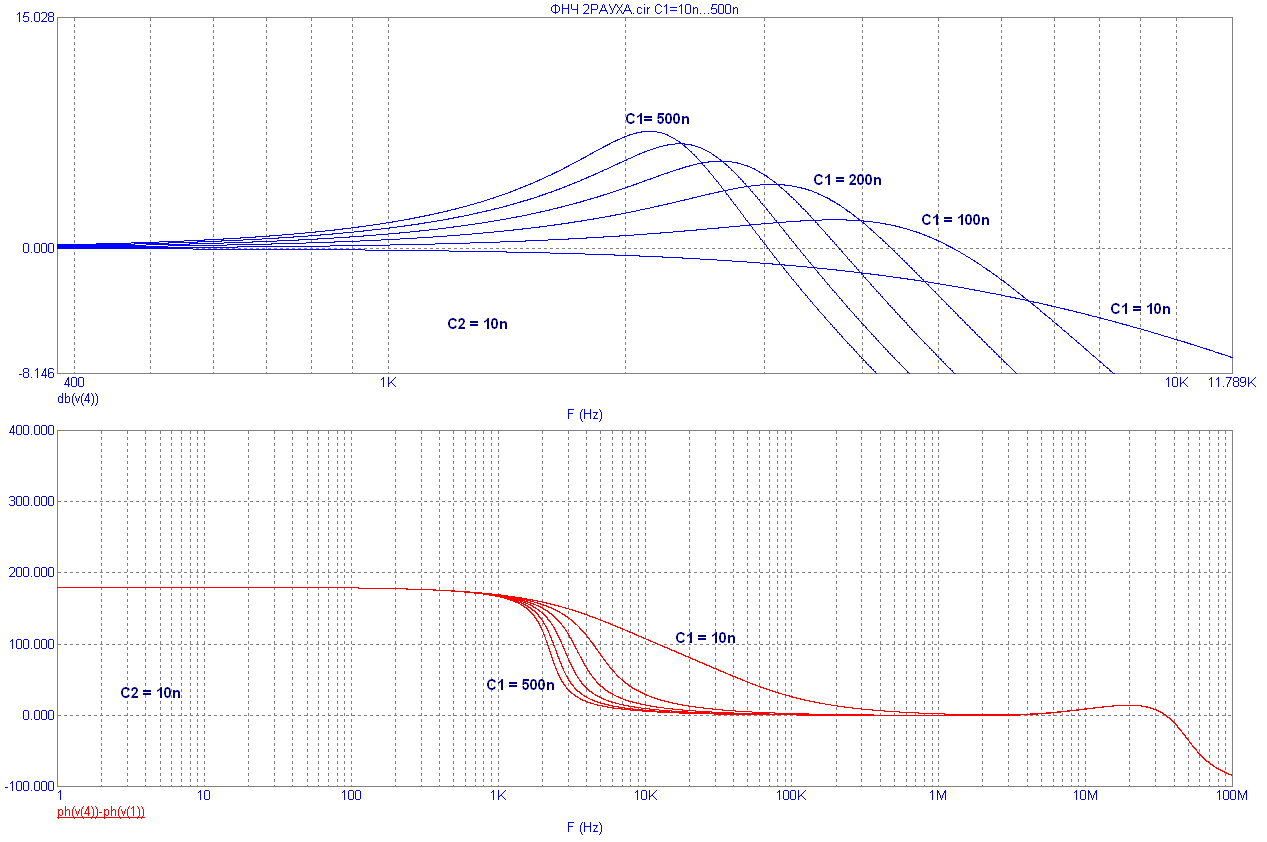
Рис.8.20

Схему рис.8.18 можно дополнить интегрирующим RC звеном, получив фильтр третьего порядка без потери устойчивости – рис.8.21.

Рис.8.21

ЛАХ и ЛФХ этого фильтра приведены на рис.8.22.

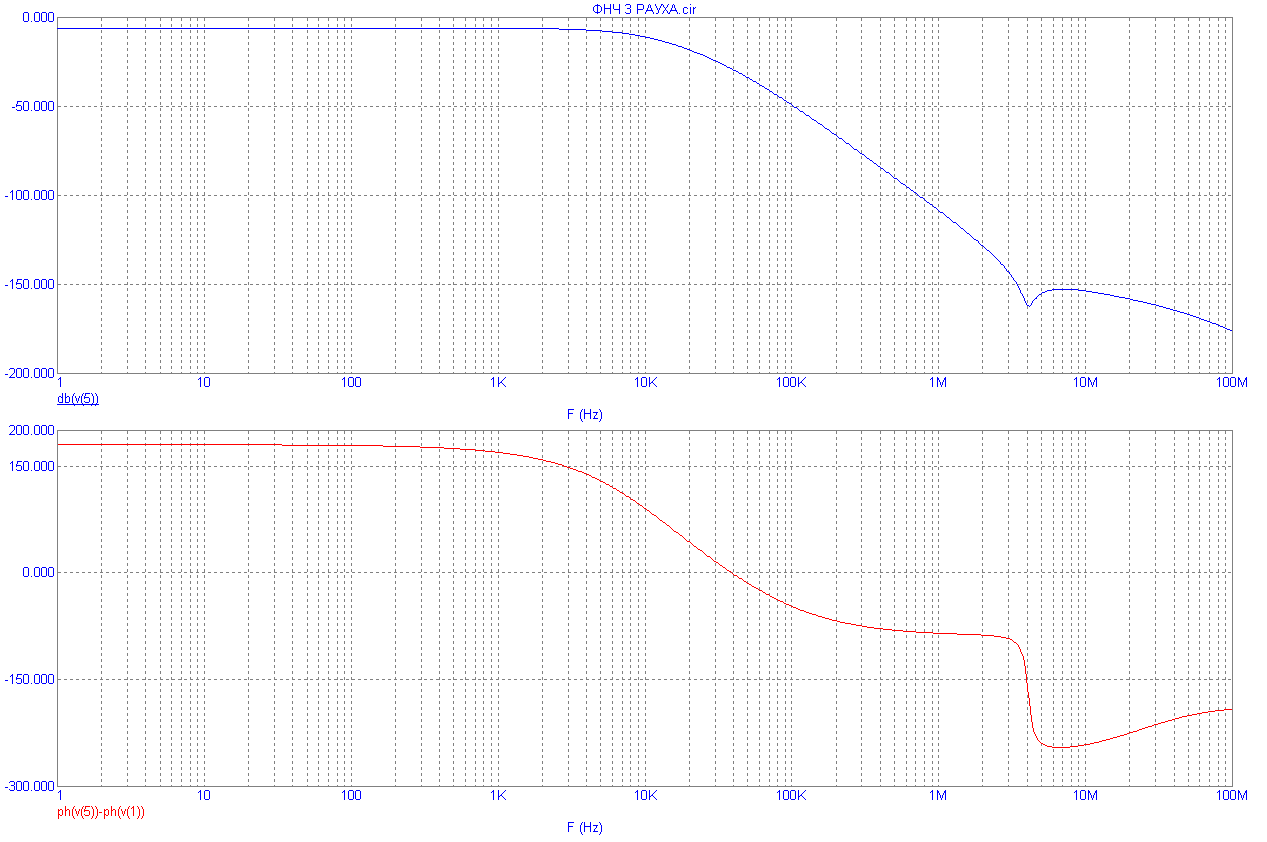
Рис.8.22

Полосовой фильтр

Схема полосового фильтра приведена на рис.8.23, а его ЛАХ и ЛФХ – на рис.8.24. Передаточную функцию фильтра описывают следующим выражением:

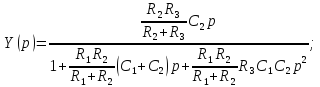(8.5)

его параметры

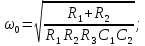
Коэффициент передачи на резонансной частоте

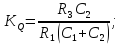
При 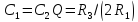. Для получения больших значений добротности следует выбирать 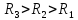и, по-возможности,

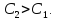
Рис.8.23

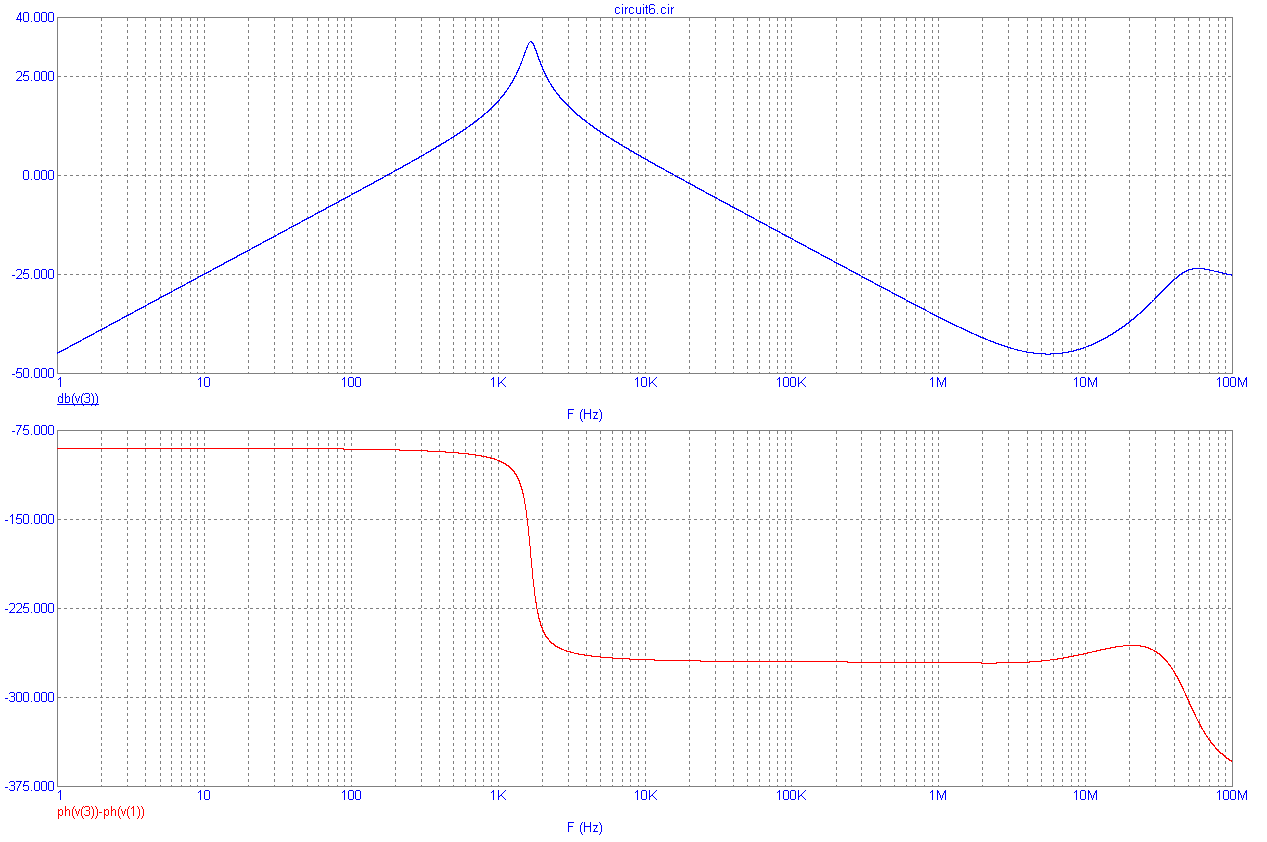
Рис.8.24

Гиратор

Идеальный гиратор был предложен Тележеном в 1948г. и может быть представлен в виде активного четырехполюсника – рис.8.25. В направлении, указанном стрелкой R_GY четырехполюсник фазу не сдвигает, а в противоположном сдвигает ее на π.

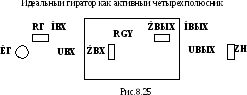
Гиратор определяют уравнениями:

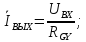
(8.6)

Уравнения (8.6) позволяют записать

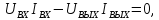
что означает, что потери в четырехполюснике отсутствуют. Следовательно, при реализации гиратора на пассивных элементах резистор 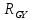должен быть чисто реактивным элементом – емкостью или индуктивностью без потерь.

Идеальный гиратор является невзаимным четырехполюсником и может быть охарактеризован матрицами сопротивлений и проводимостей

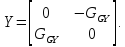
Определим сопротивления Z_ВХ и Z_ВЫХ, когда четырехполюсник нагружен на сопротивление Z_Н и к его входу подключен генератор напряжения с внутренним сопротивлением R_Г.

,

откуда

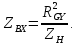
При нормировании по R_GY получаем Z_ВХ = 1/Z_Н. Поэтому гиратор называют еще инвертором положительного сопротивления (ИПС).

Аналогично, полагая, что U_ВЫХ есть источник сигнала и, закорачивая источник E_Г, находим

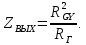
При нормировании по R_GY получаем Z_ВЫХ = 1/R_Г. Таким образом, гиратор ведет себя в обоих направлениях как инвертор сопротивления.

ФНЧ на основе гиратора

Единственным недостатком такого фильтра является необходимость двух ОУ с большим обвесом для его построения – рис.8.26. У него высокое входное сопротивление и низкая чувствительность к неточности номинальных значений элементов.

Передаточная функция фильтра

его параметры

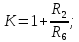
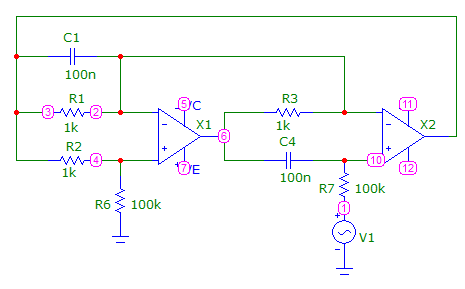
Рис.8.26

ЛАХ ЛФХ и переходные характеристики ФНЧ на гираторе приведены на рис.8.27.

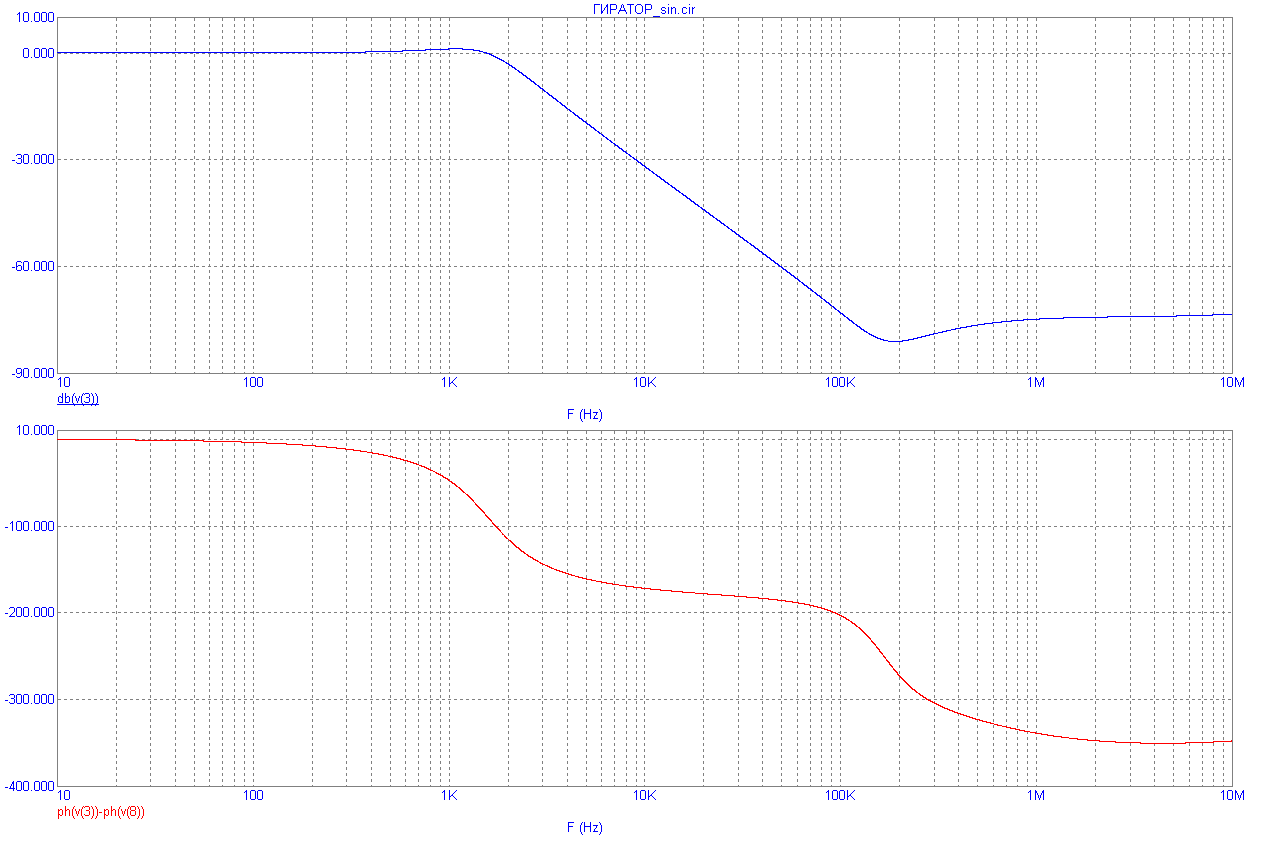
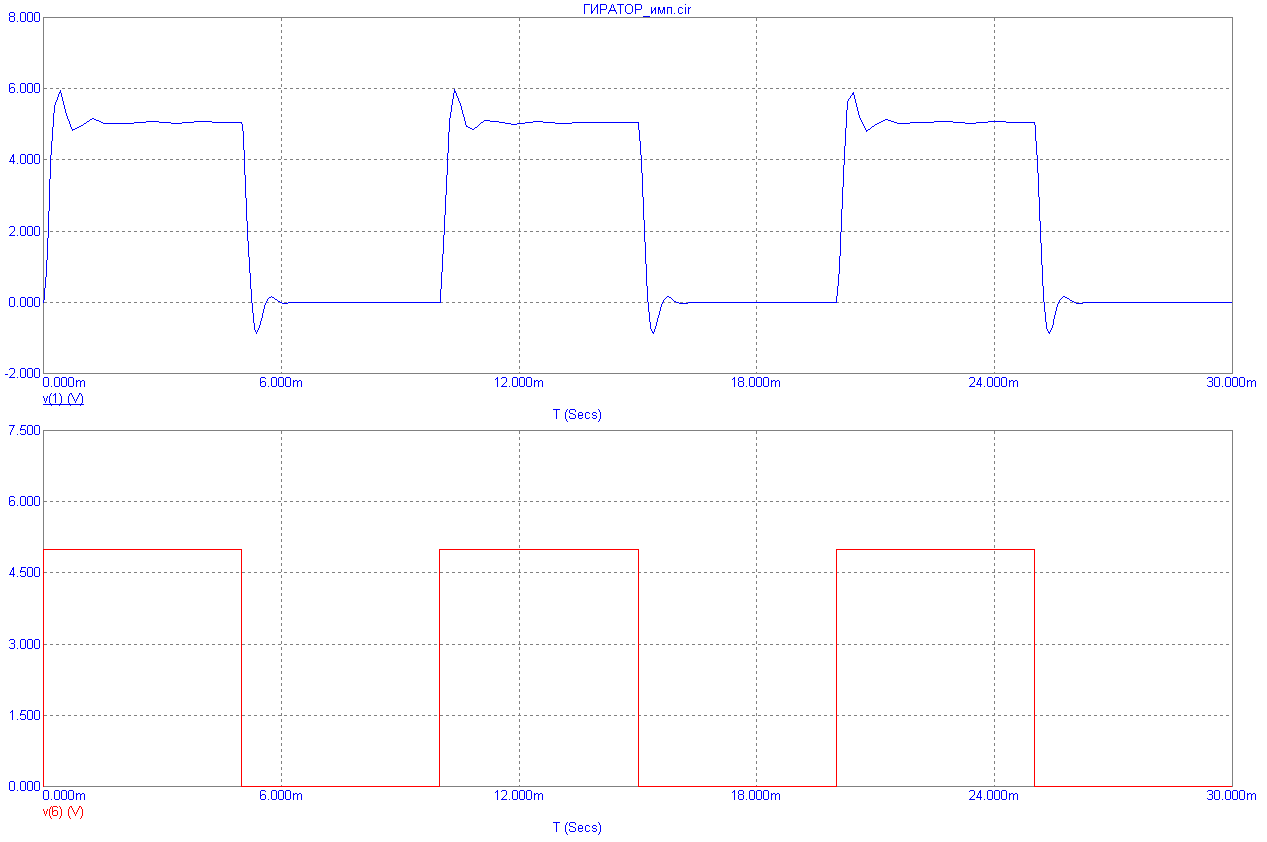
Рис.8.27

Коэффициент усиления устанавливают резистором R₂; частоту f₀ устанавливают резистором R₇; добротность Q устанавливают резистором R₁.

ФВЧ на основе гиратора

Схема ФВЧ на основе гиратора приведена на рис. 8.28, а его ЛАХ и ЛФХ приведены на рис.8.29. Передаточная функция фильтра

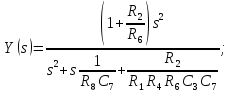
его параметры

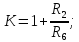
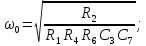
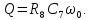
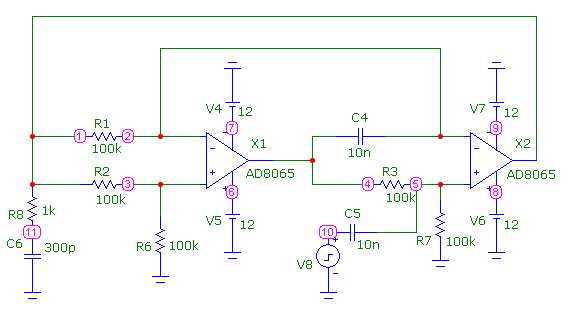
Рис.8.28

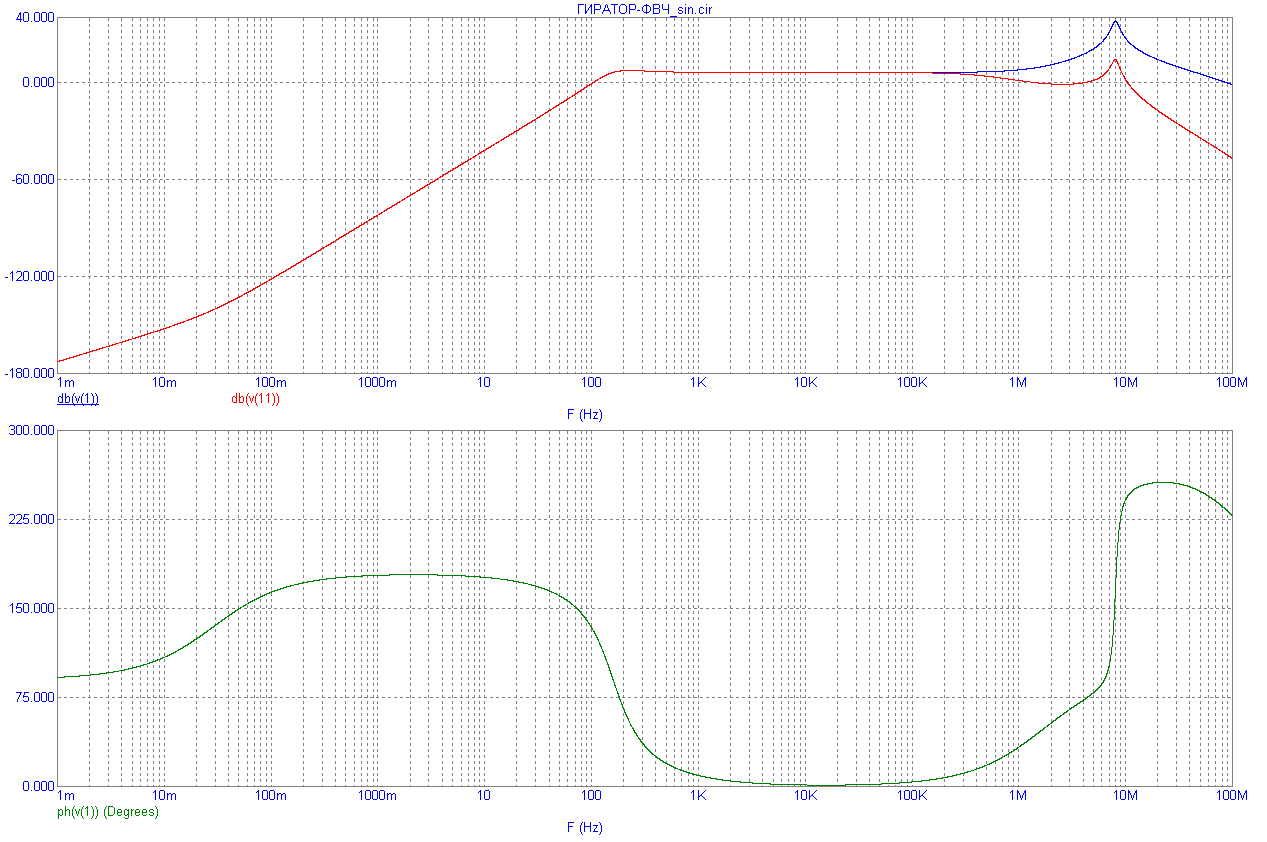
Рис.8.29

Коэффициент усиления устанавливают резистором R₂; частоту f₀ устанавливают резистором R₄; добротность Q устанавливают резистором R₈.

Фазовращатель

АЧХ фазовращателя инвариантна входной частоте, а фаза является ее функцией. На рис.8.30 приведены схемы фазовращателя на ОУ с разным фазовым сдвигом, а на рис.8.31 – их ЛАХ и ЛФХ.

Передаточная функция фазовращателя имеет вид

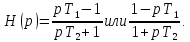
Такую характеристику можно получить из характеристики RC-звена с запаздыванием

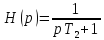
умножением знаменателя на комплексно сопряженный полином. В результате получим постоянное значение модуля, равное единице и удвоенный фазовый сдвиг:

Это звено относится к неминимально-фазовым цепям. К таким цепям относят устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью. Действительно, по сравнению с минимально-фазовым звеном

оно будет иметь бóльшие фазовые сдвиги

⃒⃒ > ⃒⃒

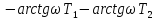при одинаковой АЧХ.

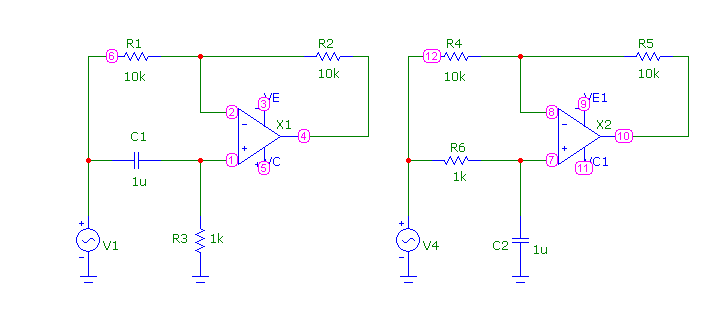
Рис.8.30

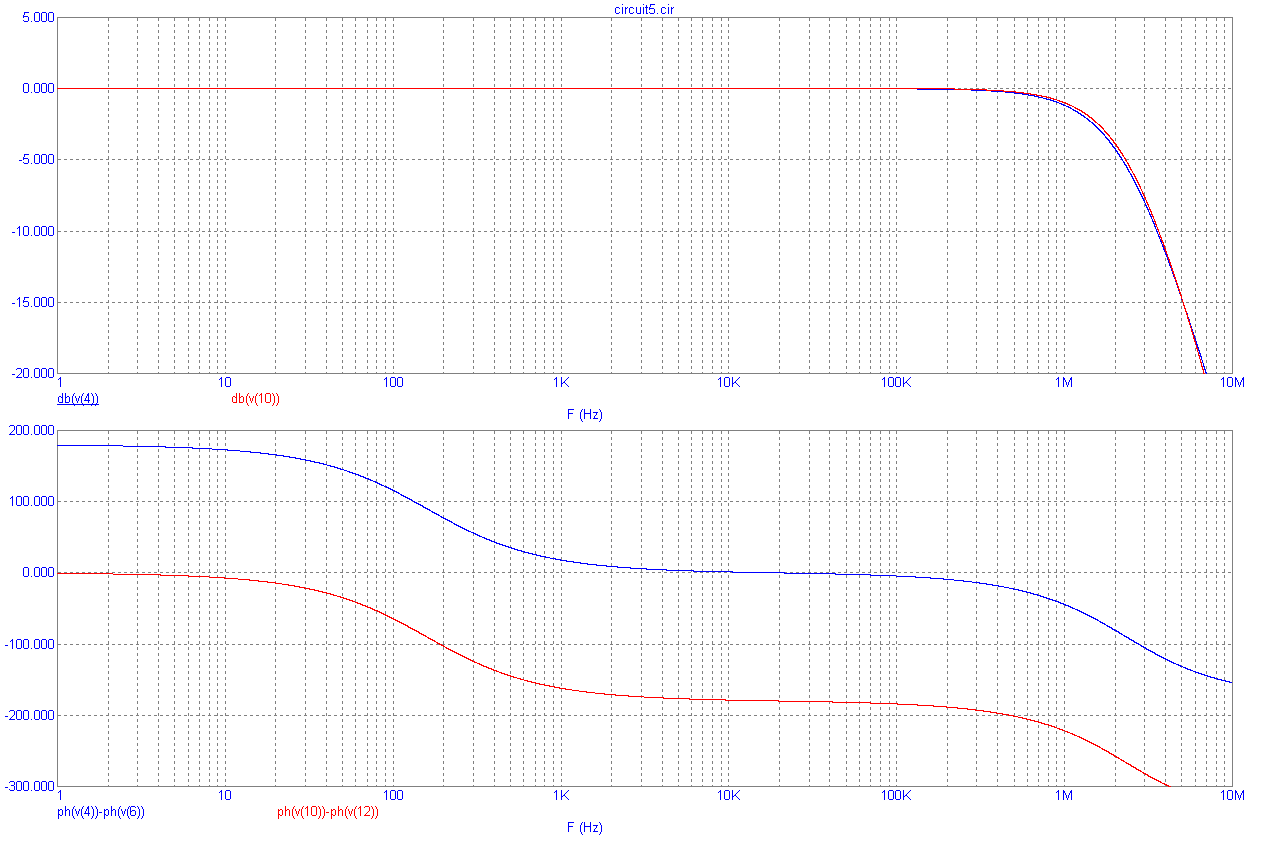
Рис.8.31

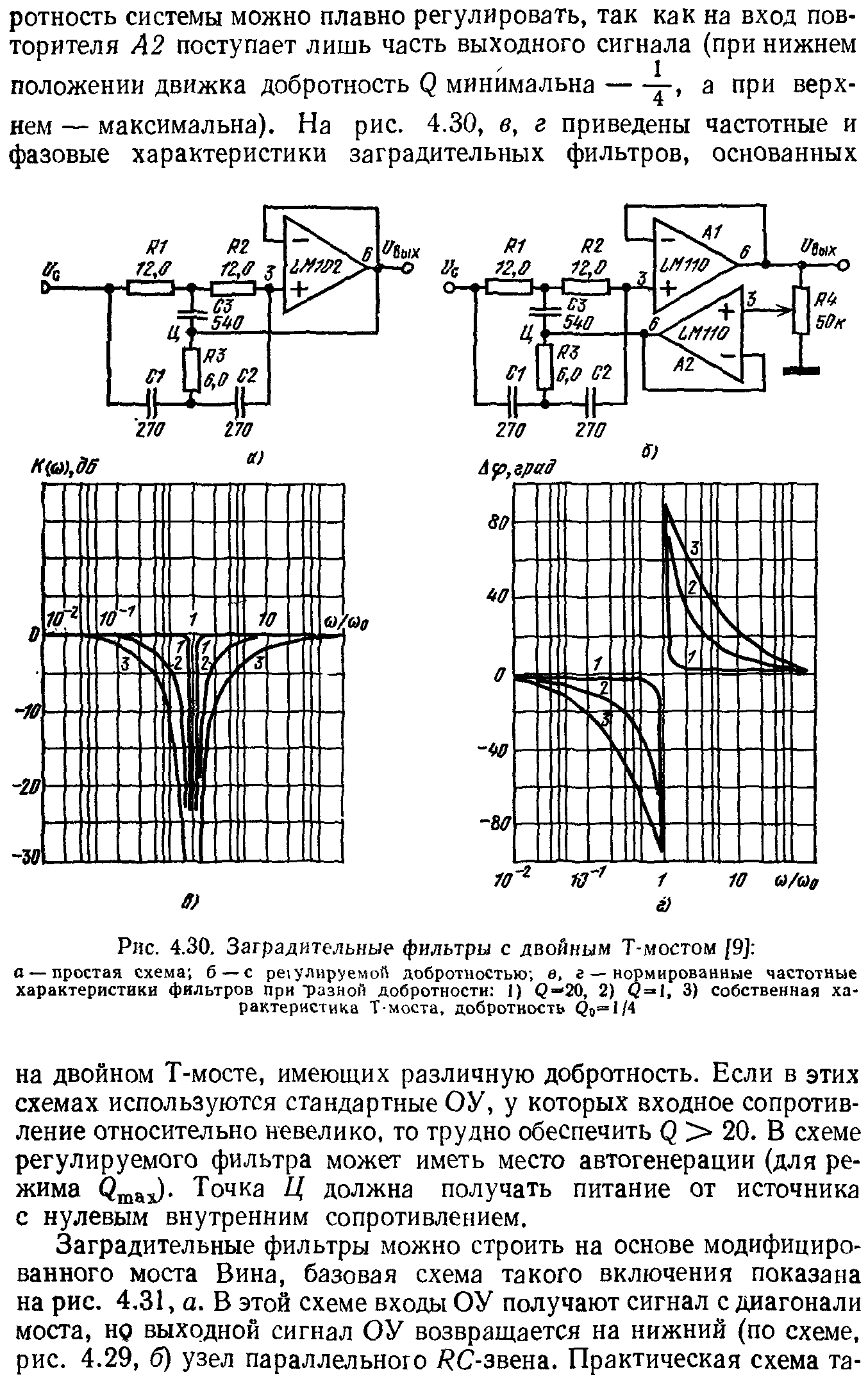
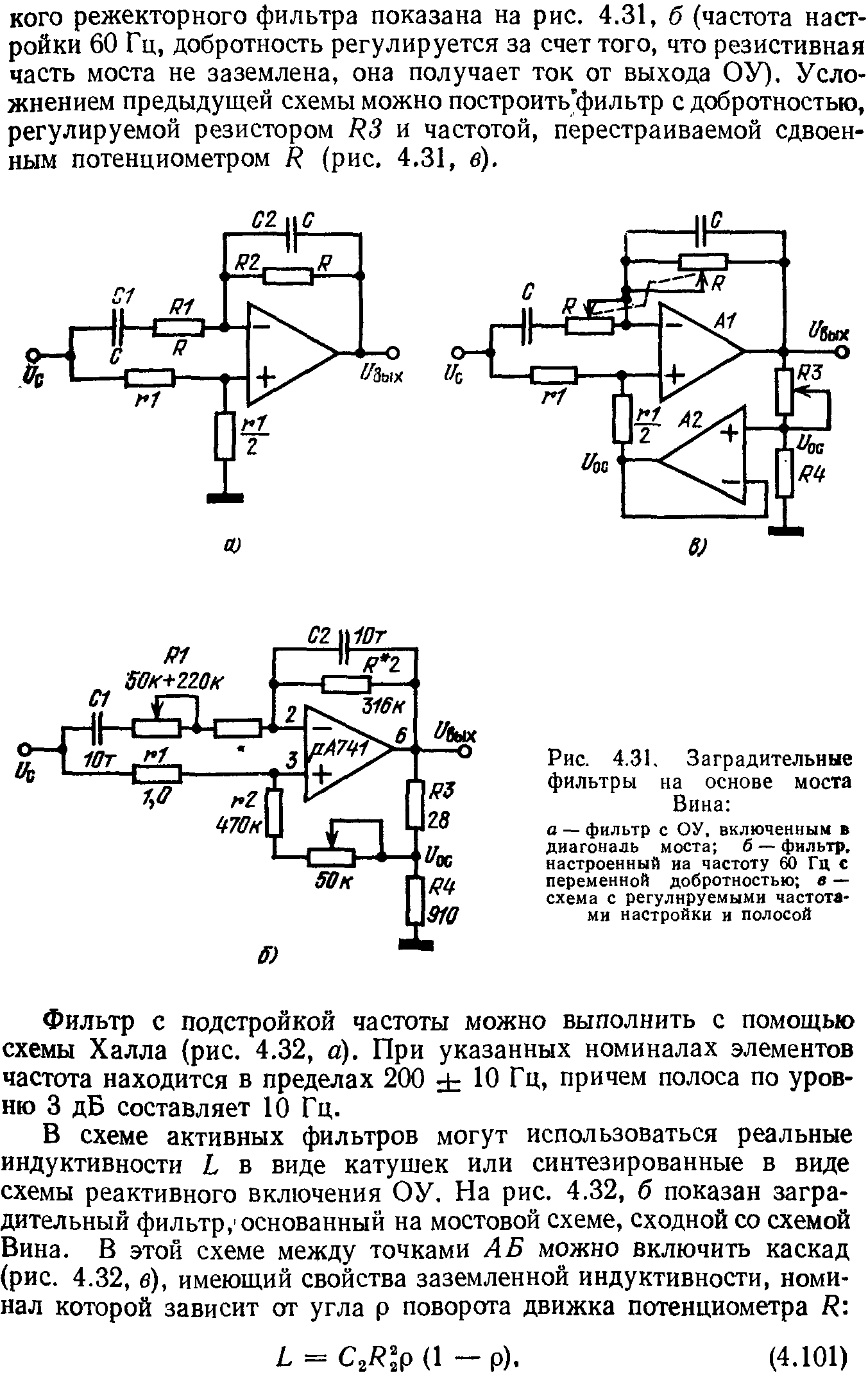
Режекторный фильтр с мостом Вина – Робинсона

Схема фильтра, его АЧХ и ФЧХ приведены на рис.8.32.

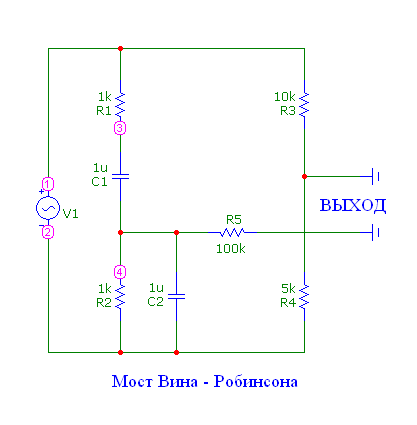
Рис.8.32

Пример реализации такого фильтра с помощью ОУ приведен на рис.8.33.

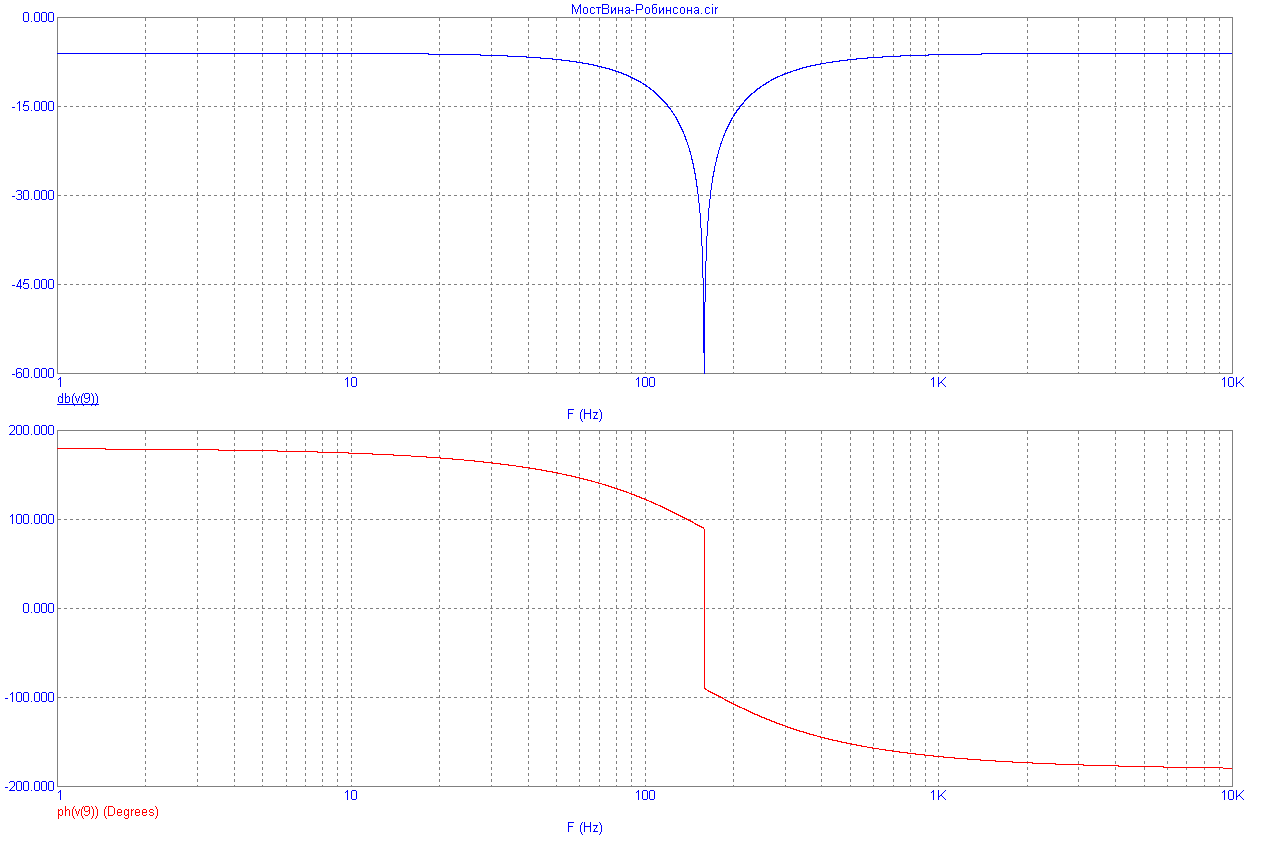
Рис.8.33

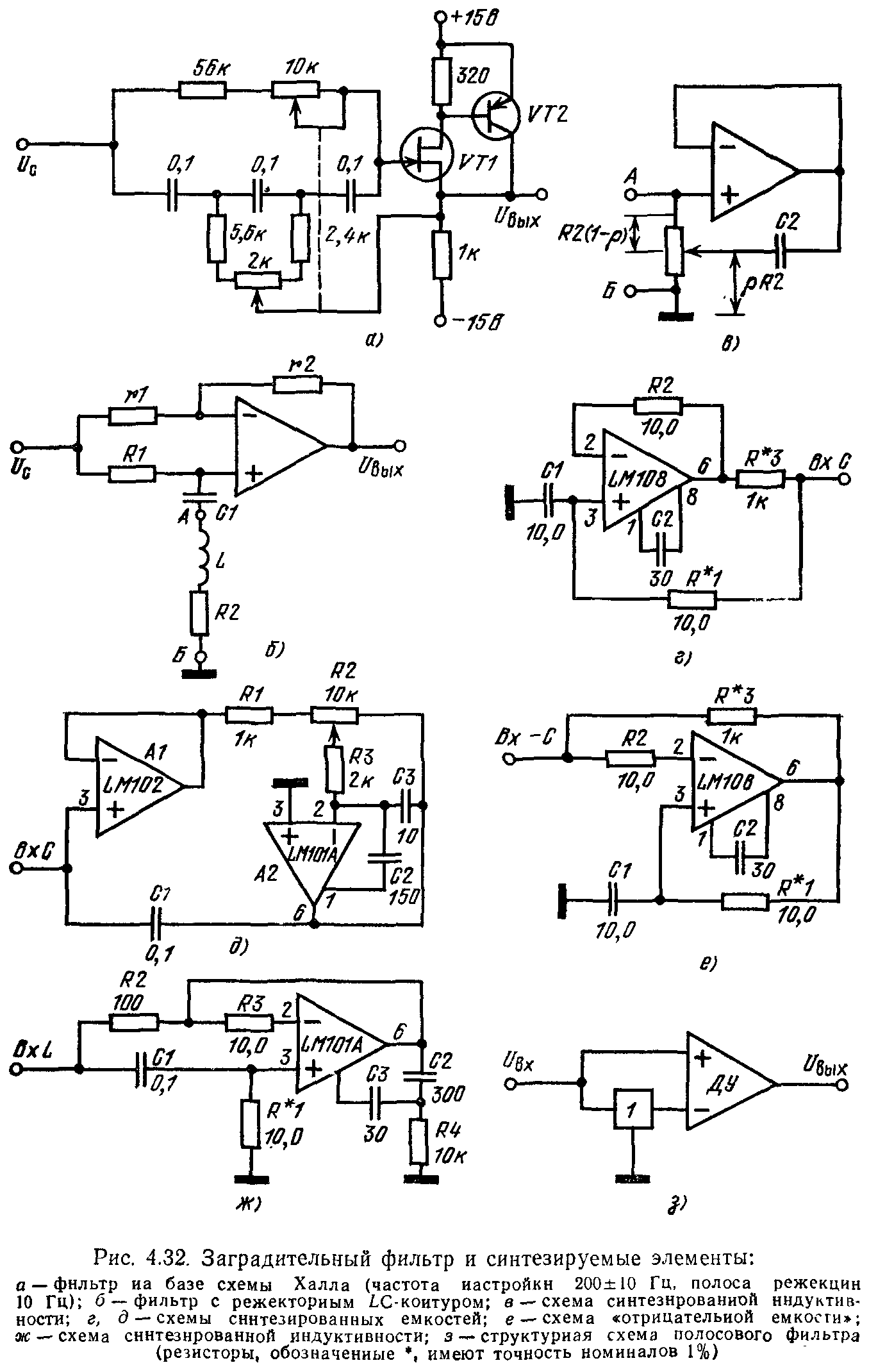
Режекторный фильтр с двойным Т-образным мостом

Схема фильтра, его АЧХ и ФЧХ приведены на рис.8.34.

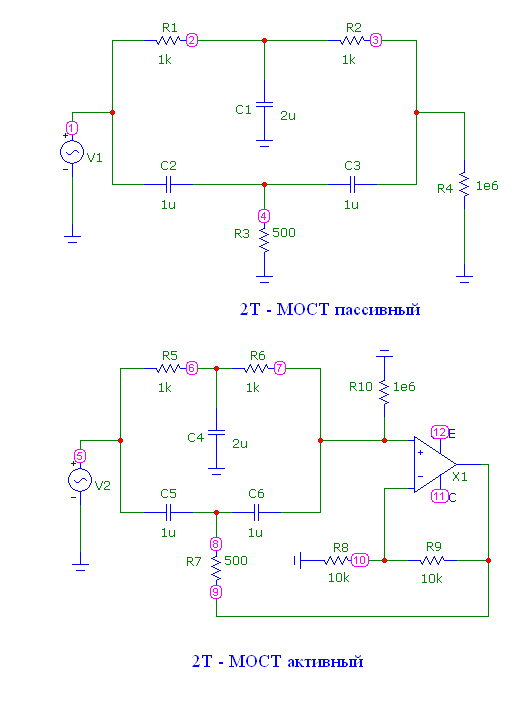
Рис.8.34

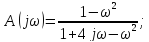
Для активного фильтра операторный коэффициент передачи записывается иначе, что позволяет реализовать более крутую характеристику режекции при k = 2.

.

Рис.8.35

38