
- •Введение
- •Предмет и задачи теории телетрафика
- •Раздел 1
- •Потоки вызовов
- •1.1 Способы определения и задания потоков вызовов
- •1.2 Основные свойства потоков вызовов
- •1.3 Основные характеристики потоков вызовов
- •1.4 Простейший поток вызовов и его свойства
- •1.5 Математическое ожидание
- •1.7 Длительность обслуживания. Поток освобождений
- •1.8 Простейшая классификация потоков
- •Раздел 2
- •Телефонная нагрузка
- •2.1 Определения телефонной нагрузки
- •2.2 Основные параметры нагрузки
- •2.3 Концентрация телефонной нагрузки
- •2.4 Способы распределения нагрузки
- •и доверительном интервале
- •Раздел 3
- •Методы расчёта пропускной способности полнодоступных включений в однозвенных коммутационных системах с потерями
- •3.2 Дифференциальные уравнения Эрланга
- •3.3 Стационарный режим. Распределение Эрланга
- •3.5 Рекуррентная формула Эрланга
- •Раздел 4
- •Системы с ожиданием
- •4.1 Обслуживание простейшего потока вызовов полнодоступным пучком с ожиданием при показательном распределении длительности занятия
- •4.2 Системы с ожиданием при постоянной длительности обслуживания
- •4.3 Расчёт пропускной способности управляющих устройств
- •4.4 Комбинированная система обслуживания Ограниченное число мест для ожидания
- •4.5 Расчёт систем с повторными вызовами
- •Раздел 5
- •5.1 Основные характеристика НПД включений
- •5.2 Типы НПД включений и выбор их структуры
- •5.3 Идеально-симметричные неполнодоступные схемы
- •5.4 Формула Эрланга для идеальной НПД схемы (третья формула Эрланга)
- •5.5 Приближённые методы расчёта пропускной способности НПД схем
- •Дополнительные и справочные материалы
- •Функции плотности и распределения вероятностей
- •Теорема Бернулли. Распределение Пуассона
- •Подробное доказательство второй формулы Эрланга
4.4 Комбинированная система обслуживания Ограниченное число мест для ожидания
Вторая формула Эрланга выведена в предположении, что число мест для ожидания не ограничено. Модель M /M /v/r →∞ , где r – число мест для ожидания. Рассмотрим случай, когда r<∞ . При этом система обслуживания вызовов является комбинированной: с ожиданием и с потерями.
M / M /v /r<∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
v [1−( |
A |
)r ] |
|
|
|
|
|||||||||||
P (γ>0)= |
|
|
v |
|
|
|
|
||||||||||||||||
|
(v−A) |
|
|
|
|
A r |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
+A [1−( |
|
) |
] |
|
|
|||||||||||
|
|
|
|
|
Ev , v ( A) |
v |
|
|
|||||||||||||||
|
Учитывая, что A<v |
|
при |
|
r=∞ |
это выражение преобразуется в |
|||||||||||||||||
выражение для P (γ>0) |
|
|
Эрланга. При |
r=0 |
комбинированная система |
||||||||||||||||||
преобразуется в систему с явными потерями и |
P (γ>0)=0 . Если вызов |
||||||||||||||||||||||
поступит в момент времени, когда заняты все |
v линий и все r мест для |
||||||||||||||||||||||
ожидания заняты, то вызов теряется. |
|
|
|||||||||||||||||||||
|
Вероятность потерь определяется из выражения: |
||||||||||||||||||||||
|
|
|
(v−A) ( |
A |
)r |
|
|
|
|
|
|
|
|
|
|
||||||||
P= |
|
|
v |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
||||
[ |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v−A |
|
|
|
|
|
A r |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Ev ( A) |
+A |
1−( |
v |
) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
При |
|
|
r=∞ |
|
потери равны нулю, так как |
A<v . |
||||||||||||||||
|
При |
|
|
r=0 |
это выражение преобразуется в первую формулу Эрланга. |
||||||||||||||||||
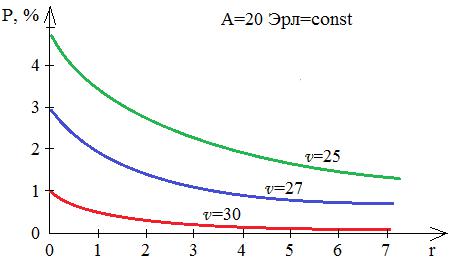
Зависимость вероятности потерь от числа мест ожидания.
Добавление незначительного числа мест для ожидания может значительно снизить потери.
Перейти к оглавлению>>> |
strelnikov.ws |
84 |

4.5 Расчёт систем с повторными вызовами
Рассматривая в предыдущих разделах системы с явными потерями, мы делали одно предположение, которое на практике не выполняется: мы считали, что вызов, поступивший на систему в момент занятости всех линий, теряется и никакого воздействия на коммутационную систему не оказывает.
Модель Эрланга:
АТС |
|
АТС |
|
АТС |
||||||
|
|
|
|
|
|
|
|
|
|
|
На практике потерянный вызов в большинстве случаев приводит к повторным вызовам.
Модель с повторными вызовами:
|
|
|
|
|
|
|
|
|
|
АТС |
|
|
АТС |
|
|
|
|
АТС |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Повторные вызовы сильно искажают картину занятости системы связи. Явление повторных вызовов представляет собой в некотором роде явления положительной обратной связи: случайное переполнение системы (потеря первичного вызова) вызывает увеличение интенсивности потока вызовов (к потоку первичных вызовов добавляется поток повторных вызовов). Известны случаи, когда из-за повторных вызовов связь «парализовывалась».
На входы коммутационной системы поступает простейший поток первичных вызовов с параметром λ . Если первичный вызов застал все v линий полнодоступного пучка занятыми, то абонент начинает повторять вызовы с интенсивностью α .
Перейти к оглавлению>>> |
strelnikov.ws |
85 |

|
Первичный |
|
|
|
вызов |
1−H 1 |
|
|
H 1 |
||
|
|
|
|
j α |
КС |
i1 |
Полнодоступный |
|
v |
пучок |
|
|
H 2 |
|
|
|
Повторный |
1−H 2 |
|
|
вызов |
|
|
|
Обозначим через |
j – число источников повторных вызовов. Тогда |
|
параметр потока повторных вызовов j α . Длительность обслуживания любого вызова (первичного или повторного) при занятии линии — величина случайная, распределённая по показательному закону с параметром β .
Рассматривается комбинированная система обслуживания — с явными и условными потерями. Источник, послав первичный вызов и получив отказ из-за
занятости всех линий, с вероятностью |
H 1 повторяет его, а с вероятностью |
||||||
1−H 1 |
отказывается от дальнейших попыток установления соединения. |
||||||
Повторный вызов с вероятностью |
H 2 |
повторяет вызов и с вероятностью |
|||||
1−H 2 |
отказывается от установления соединения. Вероятности H 1 и H 2 |
||||||
характеризуют меру настойчивости источников вызовов. |
|||||||
Состояние системы обслуживания определим двумя случайными |
|||||||
переменными: |
|
|
|
|
|
||
i – число занятых линий, i= |
|
; |
|
|
|
|
|
0,v |
|
|
|
|
|||
j – число источников, повторяющих вызовы, |
j= |
|
. |
||||
0,∞ |
|||||||
Вероятность данного состояния обозначим |
Pi j . Как и раньше, мы |
||||||
рассматриваем установившийся режим. |
|
|
|
|
|||
Перейти к оглавлению>>> |
strelnikov.ws |
86 |

Диаграмма состояний и переходов процесса обслуживания:
|
|
|
|
|
|
|
|
α (1−H 2) |
|
2 α (1−H 2) |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ H 1 |
|
|
|
|
|
|
|
λ H 1 ... |
|
|
|
|
|
v , 0 |
|
v , 1 |
|
|||||||||||
v |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
λ |
|
|
v β |
α |
λ |
|
|
v β |
|
|
2 α |
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
: |
|
|
|
|
|
: |
|
|
|
|
|
|
||||
|
|
: |
|
|
|
|
|
: |
|
|
|
|
|
|
||||
|
|
|
|
λ (i+1) β α λ (i+1) β |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
i , 0 |
|
|
|
|
i , 1 |
|
|
|||||||
i |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
λ |
|
|
i β |
α |
λ |
|
|
i β |
|
|
2 α |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
: |
|
|
|
|
|
: |
|
|
|
|
|
|
||||
|
|
: |
|
2 β |
|
|
: |
|
2 β |
|
|
|
||||||
|
|
|
|
λ |
α |
λ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1, 0 |
|
|
|
|
1, 1 |
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
λ |
|
|
β |
α |
λ |
|
|
β |
2 α |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0, 0 |
|
|
|
0, 1 |
|
|||||||||
0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j α (1−H 2) |
( j+1) α (1−H 2) |
|||||||
|
|
|
|
|
|
|||
λ H 1 |
|
|
λ H 1 |
... |
||||
v , j |
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
( j+1) α
λ v β
:
:
j α λ (i+1) β |
|
||||||
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i , |
j |
|
||||
|
|
|
|
|
|
|
( j+1) α |
|
λ |
|
: |
|
i β |
||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
j α |
λ |
: 2 β |
|
||||
|
|
|
|
|
|
|
... |
|
1, |
j |
|
||||
|
|
|
|
|
|
|
( j+1) α |
j α |
λ |
|
|
|
β |
||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
0, |
j |
|
||||
|
|
|
|
|
|
|
|
0 |
1 |
j |
j |
По вертикальной оси — число занятых линий.
По горизонтальной оси — число источников, повторяющих вызовы.
Перейти к оглавлению>>> |
strelnikov.ws |
87 |
Состояние |
i , j |
– вероятность перехода за |
t при i занятых |
линиях (i<v) и |
j |
источниках повторных вызовов. |
|
Вероятность ухода из i ,' j : |
|
||
–Вероятность поступления первичного вызова λ t (поток первичных вызовов простейший);
– |
Вероятность поступления повторного вызова |
j α t |
. Так как |
i<v |
, |
||||||||||||||
|
то занимается свободная линия и уменьшается на единицу число |
|
|
||||||||||||||||
|
источников повторных вызовов. Система из состояния |
i , |
j переходит в |
||||||||||||||||
|
состояние |
i+1, j−1 ; |
|
|
|
|
|
|
|
|
|
|
|||||||
– |
Вероятность освобождения одной из занятых линий i β |
t . |
i , j |
|
|||||||||||||||
|
В установившемся режиме система будет находиться в состоянии |
, |
|||||||||||||||||
если вероятность ухода из состояния равна вероятности возращения в это |
|
||||||||||||||||||
состояние. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(λ+i β+ j α) Pi , j=λ Pi−1, j+(i+1) β Pi+1, j+( j+1) α Pi−1, j+1 |
|
|
|
||||||||||||||||
i= |
|
|
; |
j= |
|
; |
P−1, |
j=Pi , −1=0 |
. (*) |
|
|
|
|
|
|
|
|||
0, v−1 |
0, ∞ |
|
|
|
|
|
|
|
|||||||||||
|
Вероятности ухода и возращения в |
v j переходов за |
t |
при |
v |
|
|||||||||||||
занятых линиях и |
|
j |
|
источниках повторных вызовов. |
|
|
|
|
|
|
|||||||||
|
Уход из |
v j |
: |
|
|
|
|
|
|
v , |
j |
|
|
|
|
|
|||
– |
Если первичный вызов поступит в состоянии |
, то источник, |
|
||||||||||||||||
|
получив отказ в соединении, с вероятностью |
H 1 |
перейдёт в число |
|
|||||||||||||||
|
повторяющих вызовы (величина j |
увеличится на 1), а с вероятностью |
|||||||||||||||||
|
(1−H 1) |
он покинет систему обслуживания. Вероятность перехода - |
|
||||||||||||||||
|
λ H 1 |
t ; |
|
|
|
|
v , j |
|
|
|
|
|
|
|
|
|
|
||
– |
Если в состоянии |
поступит повторный вызов, то с вероятностью |
|||||||||||||||||
|
H 2 |
он будет повторять, а состояние системы не изменится, а с |
|
|
|||||||||||||||
|
вероятностью |
(1−H 2) |
повторный вызов покинет систему |
|
|
||||||||||||||
|
обслуживания и величина |
j уменьшится на единицу. Вероятность |
|
||||||||||||||||
|
перехода — |
|
j α (1−H 2) |
t . |
|
|
|
|
|
|
|
|
|||||||
|
В установившемся режиме для состояния v , |
j |
запишем систему |
|
|||||||||||||||
уравнений вероятностей состояний: |
|
|
|
|
|
|
|
|
|||||||||||
[λ H 1+v β+ j α (1−H 2)] Pv , j=...
...=λ Pv−1, j+λ H 1 Pv , j−1+( j+1) α Pv−1, j+1+( j+1) α (1−H 2) Pv , j+1 (**)
Системы уравнений (*) и (*) необходимо дополнить условием нормировки:
v ∞
∑ ∑ Pi , j=1 (***)
i=0 j=0
Перейти к оглавлению>>> |
strelnikov.ws |
88 |

Система (*), (**) и (***) имеет аналитическое решение только для v=1 и v=2 . В других случаях эта система решается численными методами на ПЭВМ. Составлены таблицы для определения характеристик качества обслуживания.
Приближённый метод расчёта:
Рассмотрим полнодоступный пучок из v линий, на который поступает простейший поток первичных вызовов с параметром λ .
F 1(t)=1−e−λ t , |
F 2 (t)=1−e−β t , β – параметр потока освобождения |
||
линий. |
|
|
v |
1 |
2 |
3 ... |
|
λ → 0 |
0 |
0 ... |
0 |
Примем за единицу времени среднюю длительность одного занятия одной линии =1β=1 → β=1 . Обозначим через ρ – интенстивность повторных
вызовов. Тогда средняя длительность между двумя повторными вызовами : ρ1 . Обычно ρ β :
Так, если β=1 , то |
ρ=20, 30 . |
То есть если β1=100 |
сек , то ρ1=10 сек |
Длительность времени, в течение которого абонент делает повторные попытки, фактически является временем ожидания освобождения линий. Поэтому систему с повторными вызовами можно рассматривать как систему с ожиданием.
Обслуживание простейшего потока полнодоступным пучком линий при экспоненциальном законе распределения времени занятия — вторая формула
Эрланга. По известным Y = |
λ |
и v>Y определяется среднее время |
β |
ожидания на один поступивший (успешный) вызов γ̄ .
γ̄
11
ρρ
Число повторных вызовов на один успешный определится как:
Cповт= γ̄1 =γ̄ ρ
ρ
Перейти к оглавлению>>> |
strelnikov.ws |
89 |

Потери по вызовам есть отношение числа неуспешных вызовов к общему числу успешных и неуспешных:
P=1 γ̄ ρ +γ̄ ρ
Можно решить и обратную задачу: задано Y , P и ρ . Найти v . Тогда γ̄ рассчитывается:
γ= |
P |
и после этого определяется v . Этот метод приближённый. |
|
ρ (1−P) |
|||
̄ |
Сравним результаты расчёта потерь с учётом повторных вызовов и без учёта повторных вызовов.
То есть потери быстро возрастают с ростом α . Пусть поступившая
нагрузка Y =5.2 Эрл |
. P=0.2 . Тогда по первой формуле Эрланга требуется |
6 линий, а при α=30 |
требуется 10 линий. |
Перейти к оглавлению>>> |
strelnikov.ws |
90 |

Повторные вызовы создают дополнительную нагрузку. Пусть имеем три ступени искания. Потери по вызовам заданы.
|
|
1-я ступень |
2-я ступень |
3-я ступень |
|
||||||
Y пост=? |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pв=0.5 |
|
|
Pв=0.5 |
|
|
Pв=0.5 |
|
Y пр=100 Эрл |
|
|
|
|
|
|
|
|
|||||
Конечно, нельзя определять поступающую нагрузку на 3-ю ступень как
Y пост=Y пр+Y пот=200 Эрл . Грубая ошибка! Потери задаются по вызовам, но повторные вызовы занимают коммутационные устройства на длительность в
10÷30 раз меньшую длительности разговора. В системах с повторными вызовами потери по вызовам:
Pв>Pн
Особенно опасны повторные вызовы для систем с централизованными управляющими устройствами, так как они занимаются на одно и то же время для обслуживания и первичного и повторного вызовов.
tсрКС tпвКС
tсрУУ =tУУпв
КС
УУ
Так, если на линии, включённые на выходы семизвенной коммутационной системы, нагрузка из-за повторных вызовов возрастает на 10%, то на УУ она удваивается.
Для подсчёта полнодоступных пучков с повторными вызовами есть таблицы в книге: Г. Л. Ионин, Я. Я. Седов - «Таблицы вероятностных характеристик полнодоступного пучка при повторных вызовах», изд. «Наука», 1970 г.
Таблицы имеют следующий вид:
n=Y |
|
v=28 |
... |
Таблицы составляются для фиксированных |
||
v |
|
|
|
|
|
значений T и u |
|
|
|
|
|
||
C1 |
|
P |
... |
|
||
|
̄ |
|
|
|
|
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
̄ |
– среднее число повторных вызовов на |
|
|
|
|
|
C1 |
|
|
|
|
|
|
один поступивший (повторный и первичный) |
|
0.35 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
P – вероятность потерь первичных вызовов |
|
|
|
|
|
|
||
|
|
|
|
|
||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейти к оглавлению>>> |
strelnikov.ws |
91 |

Первичный
вызов
ρ
γ
T =1ρ
z=ρ+γ1
ρ– параметр потока повторных вызовов;
|
1 |
– средняя длительность между повторными вызовами; |
||||||
T =ρ |
||||||||
γ – параметр потока потерянных первичных вызовов; |
||||||||
z= |
|
|
1 |
|
|
– среднее время существования источника повторных вызовов; |
||
ρ+γ |
|
|
||||||
H = |
|
ρ |
|
|
– вероятность повторного вызова (мера настойчивости абонента); |
|||
ρ+γ |
|
|||||||
u= |
1−H |
= |
γ |
– мера ненастойчивости абонента; |
||||
|
|
H |
ρ |
|||||
u=0 – абонент повторяет, пока не получит соединение; P – вероятность потерь первичных вызовов;
M – среднее число повторных вызовов, приходящихся на один первичный вызов.
Перейти к оглавлению>>> |
strelnikov.ws |
92 |
