1.3. Определение доли необнаруженных ошибок

При ошибках кратности больше 5, возможна ситуация, когда полином будет точно таким же, как и результат сложения по mod2 каких-либо разрешенных кодовых комбинаций. Тогда принятая кодовая комбинация, содержащая такой полином ошибки, будет считаться разрешенной, что приведет к искажению информации. Составим таблицу, в которой рассчитывается доля необнаруженных ошибок для заданного циклического кода.

Табл. 2. Доля необнаруженных ошибок

Кратность ошибки i	Число вариантов ошибок Сi15	Число вариантов необнаруженных ошибок bi	Доля необнаруженных ошибок
			bi / Сi15	1/2n-k
1	15		0	9,765 * 10-4
2	105		0
3	455		0
4	1365		0
5	3003	3	9,99 * 10-4
6	5005	5	9,99 * 10-4
7	6435	6	9,324 * 10-4
8	6435	5	7,77 * 10-4
9	5005	7	13,98 * 10-4
10	3003	5	16,65 * 10-4
11	1365		0
12	455		0
13	105		0
14	15		0
15	1		0
∑	2n – 1 = 32767	2k – 1 = 31

2. Определение эффективности для кода (15,5)

Исходные данные:

• задан циклический код (15, 5);

• Вероятность ошибки p_o= 5*10^-3(для канала с независимыми ошибками);

• Вероятность ошибки p_o= 5*10^-3(для канала с группирующимися ошибками);

• Минимальное кодовое расстояние d_min = 5;

• Коэффициент группирования ошибок α = 0,5.

Эффективность определяется для режима обнаружения ошибок, и для двух типов каналов по следующим формулам:

• Канал с независимыми ошибками:

• Канал с группирующимися ошибками:

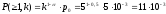
По результатам расчета можно сделать вывод, что эффективность больше на несколько порядков в канале с независимыми ошибками.

3. Определение оптимальной длинны блока циклического кода для системы рос-нп

Исходные данные:

• Вероятность необнаруженных ошибок Р_{но доп}= 5*10^-3;

• количество накопителей h = 2.

Необходимо найти такой код, который при обеспечении требуемой вероятности необнаруженных ошибокР_{но доп}обеспечивал бы максимальную скорость передачиR.

, где

– скорость кода,– скорость алгоритма.

Расчет скоростных параметров ведется по формулам:

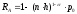
Вероятность необнаруженных ошибок рассчитывается для канала с группирующимися ошибками по следующей формуле:

R_K= 5/15 = 0,3333

R_A=1-(15*2)^1-0,5*5*10^-3= 0,9726

Рассчитаем R: R = 0,3333*0,9726= 0,3241

Все расчеты сведены в таблицу 3.

Табл. 3.

n	k	dmin	Pно	Ra	Rk	R
15	11	3	6,98*10-4
	7	5	3,38*10-5
	5	7	7,14*10-6
31	26	3	5,02*10-4
	21	5	1,21*10-5
	16	7	3,21*10-7	0,96	0,516	0,496
63	57	3	3,58*10-4
	51	5	8,66*10-6
	45	7	5,7*10-8	0,943	0,714	0,674
127	120	3	2,54*10-4
	113	5	1,53*10-6
	108	7	4*10-8	0,92	0,85	0,782
255	247	3	1,8*10-4
	239	5	2,18*10-6
	231	7	1,56*10-9	0,89	0,91	0,81
511	502	3	1,27*10-4
	493	5	1,92*10-7	0,84	0,97	0,815
	484	7	3,18*10-10	0,84	0,947	0,796

По данным расчета определяется и строится график 1 для определения оптимальной длины блока. На графике 1 указаны скорости для кодов: (31,16), (63,45), (127,108), (255,231), (511,493), (511,484).

График 1

По результатам, полученным с помощью графика, можно сделать вывод, что оптимальная длина блока равна , а максимальная скорость.