
- •Ступенчатое воздействие. Функция Хевисайда. Переходная характеристика эц, ее связь с операторной передаточной функцией. Интеграл Дюамеля.
- •Интеграл Дюамеля
- •Импульсное воздействие. Единичная импульсная функция (функция Дирака). Импульсная характеристика эц, ее связь с операторной передаточной функцией. Интеграл наложения.
- •Импульсная характеристика эц
- •Интеграл наложения
Ступенчатое воздействие. Функция Хевисайда. Переходная характеристика эц, ее связь с операторной передаточной функцией. Интеграл Дюамеля.
Единичная ступенчатая функция (функция Хевисайда) 1(t) определяется следующим образом:
1(t)
=
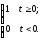 (1)
(1)
График функции 1(t) показан на рис. 1.
1(t)
1(t-)
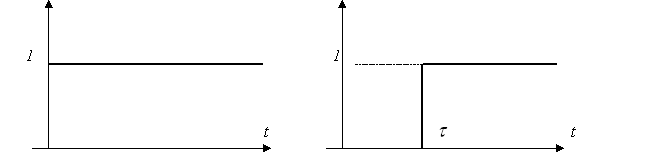 Рис.
1. Рис. 2.
Рис.
1. Рис. 2.
Функция 1(t) равна нулю при всех отрицательных значениях аргумента и единице при t . Введем в рассмотрение также смещенную единичную ступенчатую функцию
1(t-)
=
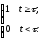
Такое воздействие включается в момент времени t = .
Напряжение в виде единичной ступенчатой функции на входе цепи будет при подключении источника постоянного напряжения U0 =1 В при t = 0 с помощью идеального ключа (рис. 8.3).
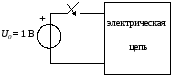 Рис.
3.
Рис.
3.
Переходной характеристикой h(t) называется реакция цепи на воздействие в виде единичной ступенчатой функции 1(t). Переходная характеристика определяется при нулевых начальных условиях.
Переходная функция характеризует цепь в переходном режиме, так как она является реакцией на скачкообразные, т.е. довольно тяжелые для любой системы воздействия. Кроме того, как будет показано ниже, с помощью переходной характеристики может быть определена реакция цепи на произвольное воздействие.
Связь переходной характеристики h(t) с операторной передаточной функцией Н(р).
По определению, операторная передаточная функция
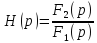 (2)
(2)
где
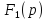 - изображение воздействия цепи (
- изображение воздействия цепи (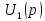 или
или
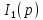 );
);
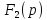 -
изображение реакции цепи (
-
изображение реакции цепи (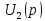 или
или
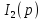 ).
).
Из (2) следует, что
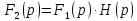 .
(3)
.
(3)
Если
в качестве воздействия на цепь подать
единичную ступенчатую функцию
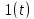 ,
то ее изображение будет
,
то ее изображение будет
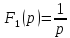 .
При этом реакцией цепи будет переходная
характеристика цепи
.
При этом реакцией цепи будет переходная
характеристика цепи
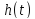 .
Изображение реакции цепи
.
Изображение реакции цепи
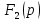 можно найти, воспользовавшись выражением
(3):
можно найти, воспользовавшись выражением
(3):
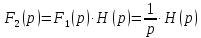 (4)
(4)
Формула
(4) выражает связь между переходной
характеристикой цепи
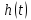 и
операторной передаточной функцией
и
операторной передаточной функцией
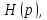 а
также позволяет определять переходную
характеристику цепи
а
также позволяет определять переходную
характеристику цепи
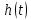 по
известной операторной передаточной
функции
по
известной операторной передаточной
функции
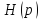 .
.
Пример.
Определить переходную
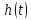 характеристику последовательной RC-цепи
(рис. 4).
характеристику последовательной RC-цепи
(рис. 4).
Воздействием
является входное напряжение u1(t)=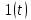 ,
а реакцией - напряжение на емкости
u2(t)=
,
а реакцией - напряжение на емкости
u2(t)=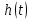 .
.
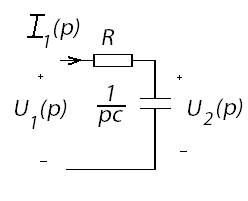
Рис. 4. Рис. 5.
Найдем
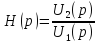 ,
для этого рассмотрим операторную схему
замещения RC-контура
при нулевых начальных условиях (рис.
5).
,
для этого рассмотрим операторную схему
замещения RC-контура
при нулевых начальных условиях (рис.
5).
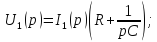
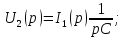
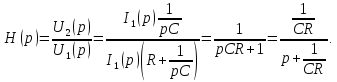
Определим
 ,
воспользовавшись (4)
,
воспользовавшись (4)
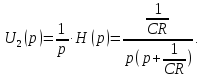
Перейдем
от изображения переходной характеристики
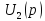 к
к
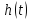 ,
воспользовавшись справочной таблицей,
которая содержит пары оригинал
изображение для различных функций
времени
,
воспользовавшись справочной таблицей,
которая содержит пары оригинал
изображение для различных функций
времени
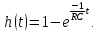
График переходной характеристики показан на рис.8.6:
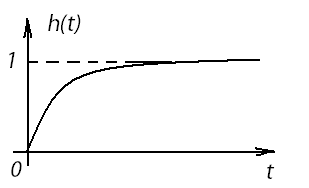
Рис. 6
