1.6. Ускорение

Ускорение характеризует быстроту изменения скорости, т.е. изменение величины скорости за единицу времени.

Вектор среднего ускорения. Отношение приращения скорости к промежутку времени, в течение которого произошло это приращение, выражает среднее ускорение:

Вектор, среднего ускорения совпадает по направлению с вектором .

Ускорение, или мгновенное ускорение равно пределу среднего ускорения при стремлении промежутка времени к нулю:

(1.13)

В проекциях на соответствующие координаты оси:

или

(1.14)

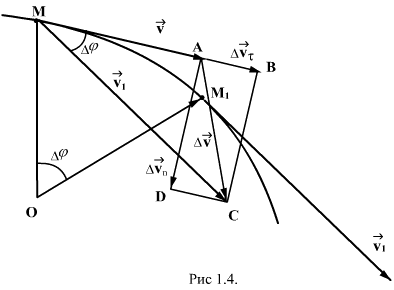
1.7. Криволинейное движение. Тангенциальное и нормальное ускорения

При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была , а в т.М₁ стала . При этом считаем, что промежуток времени при переходе точки на путииз М в М₁ настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, чтобы найти вектор изменения скорости , необходимо определить векторную разность:

Для этого перенесем параллельно самому себе, совмещая его начало с точкой М. Разность двух векторов равна вектору, соединяющему их концыравна стороне АСМАС, построенного на векторах скоростей, как на сторонах. Разложим векторна две составляющих АВ и АД, и обе соответственно черези. Таким образом вектор изменения скоростиравен векторной сумме двух векторов:

По определению:

(1.15)

Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.

Следовательно

(1.16)

Нормальное ускорение  характеризует быстроту изменения скорости по направлению. Вычислим вектор:

Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом участок криволинейной траектории можно считать частью окружности радиуса R. Треугольники МОМ1 и МВС подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах. Поэтому:

или

Но , тогда:

Переходя к пределу при и учитывая, что при этом, находим:

,

(1.17)

Так как при угол, направление этого ускорения совпадает с направлением нормали к скорости, т.е. вектор ускоренияперпендикулярен. Поэтому это ускорение часто называют центростремительным.

Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:

(1.18)

Направление полного ускорения определяется углом между векторам и:

1.8. Методические указания к решению задач по кинематике

Анализируя полученные формулы, в кинематике можно выделить четыре основных типа задач:

1. Общая прямая задача кинематики:

По известной зависимости радиуса-вектора от времени необходимо определить, векторы скоростии ускоренияи их модули v и а, нормальнуюи тангенциальнуюсоставляющую ускорения, радиус кривизны траектории R.

2. Общая обратная задача кинематики:

По известным векторам скорости или ускорениянеобходимо восстановить вид траектории, т.е. найти радиус-вектор, а затем все остальные параметры траектории, указанные в пункте 1.

3. Частная прямая задача кинематики:

По известной зависимости пути от времени необходимо найти скоростьи ускорениетела. В этом случае можно определить лишь модуль скорости и ускорения:

и .

Векторы ,,, а такжеив этих задачах не могут быть определены.

4. Частная обратная задача кинематики:

По известным зависимостям скорости или ускорениянеобходимо восстановить зависимость пути от времени: