Параграф 10: одностороние пределы слева и справа точки .

Сформулированное ранее определение относится к так называемому двустороннему пределу, что означает, что переменная приближается к своему предельному значению с любой стороны, и слева, и справа. В некоторых случаях двусторонний предел может не существовать, но существуют односторонние пределы, когда переменная приближается к только с одной стороны, или слева, или справа. В этом случае указывается соотношение или .

Запись

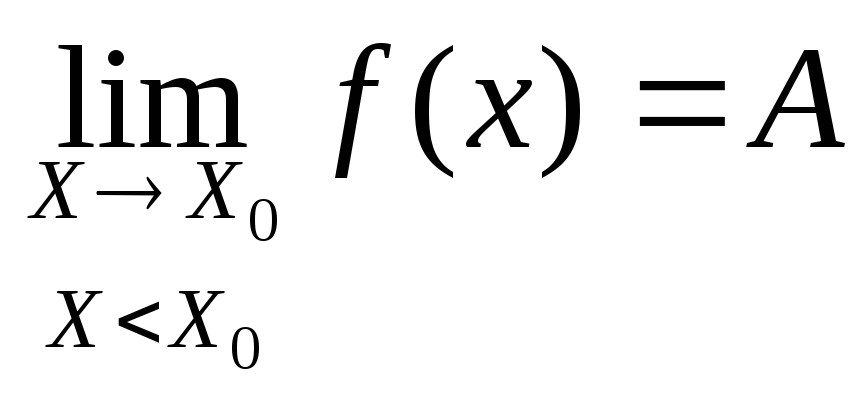– предел слева.

– предел справа

Второй вариант записи:

– предел слева.

ТЕОРЕМА:

Для того, чтобы в точке существовал двусторонний предел функции, необходимо и достаточно, чтобы существовали оба односторонних предела и они были равны между собой:

Параграф 11: предел функции на бесконечности.

Опр. 1: Постоянное число называется пределом функции при , если для любого можно указать число , что при выполнении неравенства , следует выполнение неравенства: .

Для геометрической интерпретации раскроем в неравенствах модуль:

Геометрическая интерпретация определения предела:

Неравенство (1) или (1а) определяет так называемую – окрестность бесконечности.

.

Если функция имеет предел на бесконечности равный , то график функции имеет горизонтальную асимптоту

.

Параграф 12: замечательные пределы.

I.

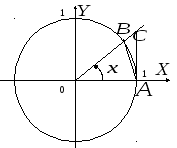
Функция – четная, поэтому можно ограничится только положительными значениями и т. к. , то можно ограничится значениями в первой четверти, т. е. . Рассмотрим площади трех фигур:

.

.

–радианная мера угла.

Т. к. фигуры вложены друг в друга, то их площади связаны неравенством:

Из неравенства (2) вытекает, что при ,как меньшая величина, тоже стремиться к нулю. Из формулы (*) следует, что при .По теореме о сжатой переменной и по формуле (3) заключаем, что при .

.

II. Второй замечательный предел.

111.

Рассмотрим:

4.

5.

6.

7.

Параграф 13: сравнение бесконечно маЛых.

Сравнение бесконечно малых величин между собой определяется через предел их отношения. Пусть ибесконечно малые величины при. Правила сравнения запишем в таблицу:

	Величины одного порядка малости
	Эквивалентные величины	. Читается: эквивалентнопри.
	Величина имеет больший порядок малости по сравнению с величиной	. Читается: есть- малое по сравнению спри.
не существует	Величины не сравнимы между собой

На основании замечательных пределов можно получить таблицу эквивалентных величин при .

Заметим, что слева в формулах стоят различные функции, а сравниваются все они со степенной функцией, наиболее простой для работы.

Параграф 14. Классификация точек разрыва

Мы уже отмечали, что функция называетсянепрерывной в точке , если она определена в этой точке и. Если функция не является непрерывной в точке, то говорят, что функция имеет разрыв в точке. Разрывы функции имеют три типа и связаны с поведением функции слева и справа от точки разрыва.

1. Устранимый разрыв. Существуют левосторонний и правосторонний пределы, оба предела конечны, равны между собой, а функция не определена в точке :

.

2. Разрыв первого рода (скачок). Существуют левосторонний и правосторонний пределы, оба предела конечны, но они не равны между собой.

3. Разрыв второго рода. Один из пределов или оба обращаются в бесконечность или не существуют.

Все элементарные функции непрерывны в области своего определения.