Параграф 6: бесконечно малые величины.

В рассмотренных выше неопределенностях участвуют функции, обладающие интересными свойствами. Их как правило рассматривают более детально.

Опр. 1: Переменная называется бесконечно малой, если её пределом является нуль.

Определение на языке ε-δ: Переменная называется бесконечно малой, если для любого ε > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства:

ПРИМЕРЫ:

1.

2.

3. – не имеет предела.

ТЕОРЕМЫ О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ.

Теорема №1:

Для того чтобы переменная имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:

, где – бесконечно малая величина.

Результат следует из того, что разность есть расстояние от точки до её предела , это расстояние стремится к нулю, т. к. , и наоборот: если расстояние стремиться к нулю, то .

Теорема№2:

Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Доказательство:

Рассмотрим, например, сумму 3-х бесконечно малых.

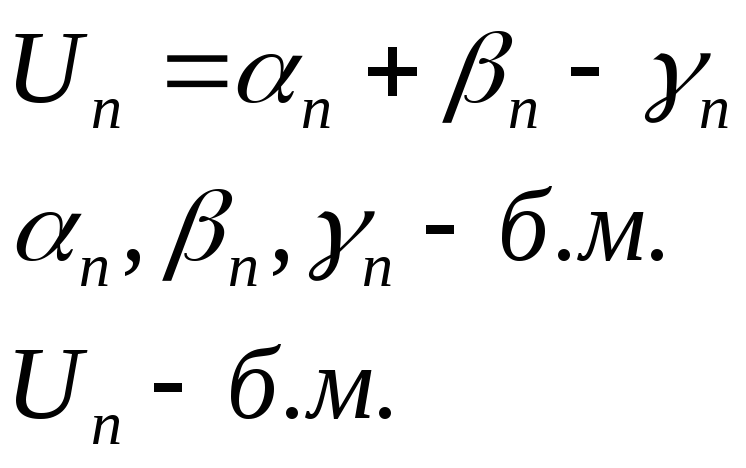
Возьмем любое ε > 0, т. к. ,то по определению существует номер n такой, что будет выполняться три неравенства:

Существует номер n, такой, что при n > N выполняется неравенство:

для , это и означает, что , Ч. Т. Д.

Опр. 2: Переменная называется ограниченной, если существуют такие m и M , что для всех выполняется равенство:

ПРИМЕР:

1. Sin n – ограниченное, т. к. |sin n| ≤ 1.

2. 

3. – не является ограниченным.

(О. П. – ограниченная переменная).

Теорема №3:

Произведение ограниченной переменной . на бесконечно малую есть величина бесконечно малая

Пусть

Требуется доказать, что:

Доказательство:

Пусть

Возьмем , т.к. – бесконечно малая, то существует номер N такой что при: ,

Тогда .

, при , следовательно, выполняется неравенства:

,

Это и означает, что: – бесконечно малая.

ПАРАГРАФ 8: БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ.

Опр. 1: Переменная , называется бесконечно большой, если для любого, сколь угодно большого, числа существует такой номер , что если

Это неравенство равносильно объединению 2-х неравенств: (где – «или»)

по другому:

Опр. 2: Объединения 2-х промежутков , называются -окрестность бесконечности.

Бесконечно большие величины при своём изменении начиная с некоторого номера попадает в окрестность бесконечности и там далее остаётся.

Пример: , если

1)

2)

-2, 4, -8, 16, -32, …

n=1 n=2 n=3 n=4 n=5

Будем различать положительные и отрицательные бесконечно большие величины

– положительные б.б.

– отрицательные б.б.

ТЕОРЕМЫ О БЕСКОНЕЧНО БОЛЬШИХ.

Теорема №1(взаимосвязь бесконечно больших и бесконечно малых величин):

Величина обратная бесконечно малой есть бесконечно большая величина, и обратно…

Доказательство:

Пусть ,

Это значит, что для любого сколь угодно большого числа существует N такой, что при следует выполнение неравенства:

Теорема №2:

Произведение бесконечно большой величины на переменную, стремящуюся к конечному пределу отличному от нуля, есть бесконечно большая величина.