Параграф 4: предел последовательности.

Говорят, что числовая последовательность {xn} имеет предел, равный a ,

если все члены этой последовательности с достаточно большими номерами сколь угодно близки к числу a .

В качестве примера, рассмотрим последовательность, представленную на рисунке.

Первый элемент последовательности x1 выбирается произвольно. Второй элемент x2 выбирается делением отрезка [x1,a] пополам. Третий элемент – делением отрезка [x2,a] пополам. И т.д.

Дадим теперь точное определение предела последовательности.

Опр1. Число a называется пределом числовой последовательности {xn} при n стремящемся к бесконечности, если для любого, сколь угодно малого, положительного числа ε >0 найдется такое, достаточно большое, натуральное число N , что при n > N выполняется неравенство

| xn -  a |< ε:

Обозначают по-разному. Посмотрим на рассмотренные выше последовательности.

Геометрическая иллюстрация показывает,

что если выбрать конкретное значение, например, ε= 0,1, все члены рассмотренной выше последовательности с номерами n > N = 3 отличаются от a меньше, чем на 0,1 (т.е. | xn  - a |<0,1 ). Если же выбрать ε в сто раз меньше, то, все равно, найдется такое значение номера члена последовательности N (например, N = 500), что все последующие члены отличаются от a меньше чем и на это ε . И.т.д.

Если последовательность имеет предел a , то говорят, что она сходится (к a ). В противном случае, говорят, что последовательность расходится.

Основные свойства предела последовательности :

Число е, гиперболические функции

Теорема. Существует предел последовательности

причем этот предел удовлетворяет неравенству 2 < a < 3.

Параграф 5. Предел действительной функции одного действительного переменного

Говорят, что предел функции f (x) при x стремящемся к x0 равен a , если в достаточно малой окрестности точки x0 значения функции f (x) сколь угодно близки к числу a . Более строго определение предела формулируется следующим образом.

Опр1. Число a называется пределом функции f (x) при x стремящемся к x0 , если для любого сколь угодно малого положительного числа δ существует такое достаточно малое положительное число ε , что в проколотой δ-окрестности точки x0 выполняется неравенство | f (x)  - a |<ε .

Число x0 называется предельной точкой.

Геометрический смысл этого определения иллюстрируется рисунком

Функция называетсянепрерывной в точке , если она определена в этой точке и. Для непрерывной функции возможен переход к пределу под знаком функции.

Предельные переходы, содержащие нуль или бесконечность, при кратко можно записать так:

, (1)

где выражение, заключенное в квадратные скобки, понимается как предельное значение.

Выражения вид , (2)

─ называются неопределенностями, что означает, что нельзя дать ответ, используя правила (1), Например, рассмотрим три функции: при. Отношение любых двух функций из указанных трех приводит к неопределенности. Однако, пределы этих отношений различны, например:

, ,.

Неопределенности (2) всегда можно перевести из одной в другую. Кроме указанных выражений неопределенностями являются предельные выражения:

.

При вычислении пределов сначала подставляется предельное значение переменной. Если выполнены условия теорем, то сразу получаем ответ. Если при подстановке получается неопределенность, то следует предварительно преобразовать выражение, а затем подставить предельное значение.

Рассмотрим несколько примеров на вычисление пределов.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10..

11. .

12. .

13.

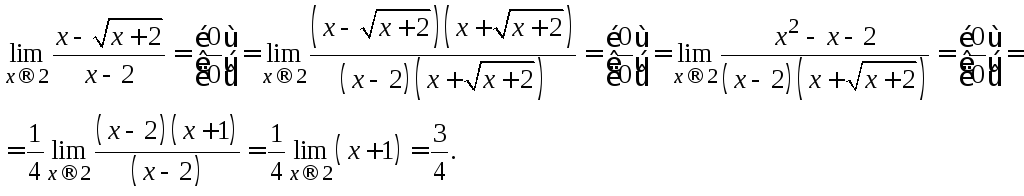
В примерах 1─3,6─8 можно сразу записать ответ. В остальных примерах первая подстановка приводит к неопределенности, поэтому: сначала проводим преобразование. Так в примере 13 мы умножили числитель и знаменатель на сопряженное выражение, что позволило затем сократить дробь. Обратите внимание, что выражение , и это позволило вынести множительза знак предела.

Проанализировав решения примеров 9–11, замечаем, что при вычислении пределов типа , приходим к пределу отношения членов со старшими степенями. Окончательный ответ зависит от соотношения степеней. Аналогичная ситуация и для выражений, содержащих дробные степени или радикалы.

Например, вычисляя , приходим к неопределенности. Выбрав в числителе и знаменателе слагаемые со старшими степенями. получаем решение:

.