1.Расчет lc-фильтра

1.1. Содержание задания

Рассчитать LC-фильтр, полагая, что его элементы имеют пренебрежительно малые потери.

Задание согласно варианту:

Тип фильтра: ПЗФ(полосно-задерживающий фильтр).

Вид аппроксимации характеристики ослабления: по Чебышеву.

Режим работы фильтра: двусторонняя нагрузка.

Гарантированное ослабление в полосах задерживания = 14 дБ.

Граничная частота полосы пропускания = 5150 Гц.

Граничная частота полосы пропускания = 9850 Гц.

Граничная частота полосы задерживания = 8750 Гц.

Допустимая неравномерность характеристики ослабления фильтра = 1,25 дБ.

Величина нагрузочного сопротивления R2 = 600 Ом.

0. 1.2.Проектирование схемы фильтра

Параметры фильтра и характеристики проектируемого фильтра находятся с помощью частотного преобразования фильтра-прототипа нижних частот (ФПНЧ).

Прежде всего необходимо определить порядок ФПНЧ, который, для фильтров с характеристиками Чебышева находится по формуле:

Где - нормированная граничная частота полосы задерживания ФПНЧ, которая рассчитывается по формуле:

Где ив свою очередь определяются по формулам:

Согласно расчетам:

Округляя n в большую сторону, получаемn = 3 – получается фильтр третьего порядка.

Схема ФПНЧ для режима двусторонней нагрузки и n = 3.

Параметры берутся из таблицы 1.9:

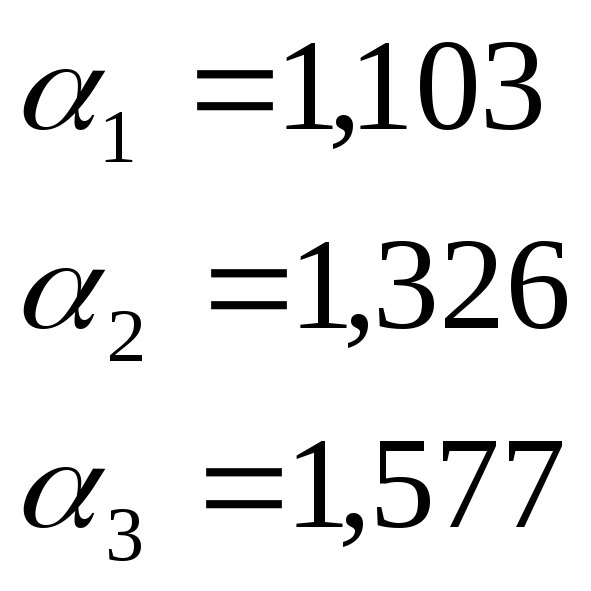
Параметры проектируемого фильтра определяются путем соответствующего пересчета параметров элементов ФПНЧ по следующим формулам:

Элементы ФПНЧ	Элементы ППФ фильтра	Формулы пересчета

Получившиеся численные выражения элементов фильтра:

Получившаяся схема фильтра:

1.3. Определение передаточной функции фильтра

Передаточная функция полиноминального ФПНЧ:

,

где - полином Гурвицаn-й степени,B– коэффициент, определяющий величину ослабления фильтра на частоте

Для ФПНЧ с характеристикой Чебышева

Пользуясь таблицей 1.12, можно определить, что идля моего фильтра равно:

Передаточная функция проектируемого фильтра H(p)находится частотным преобразованием передаточной функциифильтра-прототипа нижних частот.

Для ПЗФ используются следующие формулы:

Передаточная функция ФПНЧ	Формула преобразования	Передаточная функция фильтра H(p)

Полином V(p), полученный частотным преобразованием полинома2-го порядка, содержит два квадратичный сомножителя:

где идля ПЗФ рассчитываются по следующему алгоритму:

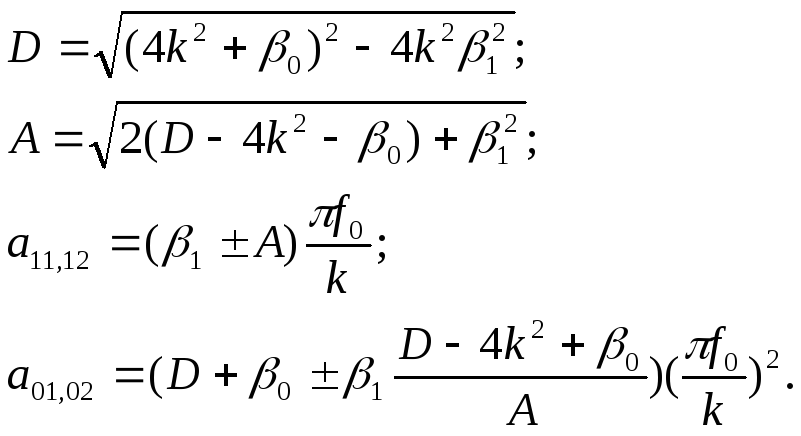
Тогда:

1.4. Расчет характеристики ослабления проектируемого фильтра

Характеристику ослабления проектируемого фильтра можно получить частотным преобразованием характеристики ослабления ФПНЧ, для аппроксимации по Чебышеву данная характеристика выглядит следующим образом:

,

где n– порядок ФПНЧ,- нормированная частота ФПНЧ,-полином Чебышеваn-го порядка. Дляn= 3,выглядит следующим образом:

Тогда

Для расчета характеристики ослабления проектируемого фильтра a(f)можно использовать прямое преобразование частоты. Для ППФ используется такое преобразование:

Следовательно, характеристика ослабления a(f), полученная использованием прямого преобразования частоты, выглядит так:

График характеристики ослабления a(f), построенный в программе Maxima