Практика 1 -2 Анализ алгоритмов.

Цель работы: знакомство с понятием анализа сложности алгоритма, получение асимптотической оценки выполняемых алгоритмом операций в зависимости от длины входа, изучение функции трудоемкости и соответствующей системы обозначений при реальных размерах входа. Основные алгоритмические конструкции программ и их анализ с точки зрения функции трудоемкости. Классификация алгоритмов на основе функции трудоемкости .

Задания

Задание №1 Алгоритм Евклида.

Найдите наибольший общий делитель (НОД) двух целых чисел a и b разными способами, используя алгоритм Евклида с вычитанием и алгоритм Евклида с делением.

Для каждого из этих двух случаев составьте блок-схему используемого вами алгоритма. Напишите и оттестируйте программы, реализующие каждый из алгоритмов. Исходные данные вводятся с клавиатуры.

Анализ опишите в виде таблицы :

Исходные данные 420 150

Шаг1 ххх ххх

Шаг2 ххх ххх

………………………………

…….. ….. ….

ШагN ---- ----

Сделайте вывод, какой из алгоритмов эффективнее и почему?

Пояснения

Первым дошедшим до нас алгоритмом в его интуитивном понимании как конечной последовательности элементарных действий, решающих поставленную задачу, считается алгоритм Евклида (III век до нашей эры). Это алгоритм нахождения наибольшего общего делителя (НОД) двух чисел (a,b).Алгоритм Евклида асимптотически оптимально решает задачу нахождения НОД(а,b). Задача нахождения НОД не утратила своей актуальности и является сегодня составной частью многих эффективных алгоритмов.

Асимптотический анализ позволяет оценивать рост потребности алгоритма в ресурсах( например, времени выполнения с увеличением объема входных данных.)

Алгоритм Евклида с вычитанием.

Даны два числа. Большее из них заменяется разностью этих чисел. Процесс повторяется, пока не останется одно ненулевое число. Это число и будет НОД исходных чисел.

Алгоритм Евклида с делением.

Большее из них заменяется остатком от деления на меньшее. Процесс повторяется, пока не останется одно ненулевое число. Это число и будет НОД исходных чисел.

Обоснование правильности алгоритма основано на свойствах НОД.

Свойство НОД : НОД(a,b)=НОД(b, a mod b),

где (a mod b) является целочисленной линейной комбинацией a и b

[Например, НОД(12,18)=6 НОД(45,72)=9]

Задание №2

Напишите алгоритм, подсчитывающий количество каких – либо букв в текстовом файле. Подсчитайте, сколько сравнений требуются этому алгоритму?

Каково максимальное возможное значение числа операций увеличения

счетчика? Минимальное такое число? Выразите ответ через число N символов во входном файле. ( N – общее число символов в файле.)

Задание №3

Напишите алгоритм, который получает на входе три целых числа, и находит наибольшее из них. Каковы возможные классы входных данных? На каком из них Ваш алгоритм делает наибольшее число сравнений? На каком меньше всего? Если разницы между наилучшим и наихудшим классами нет, то перепишите свой алгоритм с простыми сравнениями так, чтобы он не использовал временных переменных, и чтобы в наилучшем случае он работал быстрее, чем в наихудшем.

Задание №4

Напишите алгоритм, не использующий сложных условий, который по трем введенным целым числам определяет, различны ли они все между собой? Сколько сравнений в среднем делает ваш алгоритм? Обязательно исследуйте все классы входных сигналов.

Задание №5

Составить алгоритм нахождения максимального или минимального из

нескольких(3-4) чисел двумя способами. На основе составленных

алгоритмов написать программы. Провести сравнения этих алгоритмов по эффективности.

Задание №6

Напишите алгоритм, который по данному списку чисел и среднему значению этих чисел определяет, превышает ли число элементов списка, больших среднего значения, число элементов , меньших этого значения, или наоборот. Опишите группы, на которые распадаются возможные наборы входных данных. Какой случай для алгоритма является наилучшим? Наихудшим? Средним?

Если наилучший и наихудший случаи совпадают, то перепишите алгоритм так, чтобы он останавливался, как только ответ на поставленный вопрос становится известным, делая наилучший случай лучше наихудшего.

( решение этой задачи зависит от того , знаем ли мы заранее длину входных данных или она выясняется в процессе работы алгоритма.)

Задание №7

Составьте таблицу классов роста различных функций

, n, , , на некотором диапазоне значений аргумента (1,2,5,10,20,30,40,50,60,70,80,90,100)

Задание №8

Расположите следующие функции в порядке возрастания:

, , ,

Задание №9

Для приведенных пар функций f и g выполняется одно из равенств: либо f=O(g), либо g=O(f), но не оба сразу. Определите, какой из случаев имеет место.

Теоретическая часть

Задача может иметь несколько алгоритмов решения. Обязательное условие – рассматриваемые алгоритмы решают задачу правильно. Хотим ответить на вопрос, насколько каждое из этих решений эффективно.

Для ответа на этот вопрос проводим анализ алгоритмов.

С одной стороны – алгоритм должен быть как можно проще для понимания и написания по нему внятной программы.

С другой стороны хотелось бы, чтобы реализованный на компьютере алгоритм выполнялся как можно быстрее.

Эти требования противоречивы, поэтому, какому из них отдать предпочтение зависит от того, как именно мы хотим использовать эту программу – будем ли мы выполнять эту программу всего несколько раз, или нам предстоит работать с ней многократно. Так что программистам необходимо уметь оценивать и скорость работы программы , и то, когда и как мы будем их использовать.

Отсюда вытекает необходимость измерения временной сложности алгоритма. Под временной сложностью алгоритма подразумевается “время” выполнения алгоритма, измеренное в шагах, которые необходимо выполнить алгоритму для получения окончательного результата. ( Измерение времени в шагах естественно не равно времени выполнения программы).

Оцениваем число операций, выполняемых алгоритмом. От этого будет зависеть количество времени для его выполнения. Число операций измеряет относительное время выполнения алгоритма.

Но это еще не все. Необходимо учесть зависимость числа операций в каждом конкретном алгоритме от размера входных данных. Пусть есть два алгоритма А и B. При небольшом размере входных данных алгоритм А может требовать меньшего числа операций, чем алгоритм B, но при росте объема входных данных все может быть наоборот, то есть алгоритм B может требовать меньшего числа операций, чем алгоритм А. И все это необходимо учитывать.

Два самых больших класса алгоритмов.

Алгоритмы

/ \

С повторениями Рекурсивные

| |

Циклы и условные выражения декомпозиция и применение к отд.частям

|

Оценка числа операций колич. операц. для разбиения на части

внутри цикла + число + выполнение алгоритма на каждой

повторений цикла из частей + объединение

Для начала посчитайте в вашей программе количество различных операций: есть ли в вашей программе присваивания, сравнения, приращения и сколько их.

Анализируя свой алгоритм, проверьте, сколько у вас операций сравнения и арифметических операций. Операторы сравнения проверяют равенство или неравенство величин между собой.

Арифметические операции делятся на две группы – первая группа – сложение, вычитание, увеличение и уменьшение счетчика.

Вторая группа – умножение деление, взятие остатка по модулю.

Есть еще третья группа – логарифмы, тригонометрические функции. Они еще более времяемкие.

Замечание Целочисленное умножение или деление на степень двойки приводит к обычному сдвигу, что эквивалентно сложению.

Сравнение алгоритмов на основе функции трудоемкости

Итак, под трудоемкостью алгоритма для данной конкретной проблемы, заданной множеством D, понимают количество элементарных операций, задаваемых алгоритмом в принятой модели вычислений. В качестве модели вычислений рассматривают абстрактную машину, имеющую процессор с фон- Неймановской архитектурой, адресную память и набор элементарных операций, соответствующий языкам высокого уровня. Такая модель вычислений называется машиной с произвольным доступом к памяти (RAM).

Функция трудоемкости f_A (D) – это отношение, которое связывает входные данные с количеством элементарных операций. Значением этой функции является целое положительное число.

Опыт показывает, что количество элементарных операций, задаваемых алгоритмом, то есть значение f_A (D) на входе длины n, где n=|D| , не всегда совпадает с количеством операций на другом входе такой же длины. (потому что существует много множеств D длины n – то есть может быть много различных входных наборов данных)

Поэтому при анализе алгоритмов различают худший случай, лучший случай, и средний случай.

Худший случай – это наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Лучший случай – это наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Для получения значений функции трудоемкости f_A (D) определили элементарные операции, используемые в языках высокого уровня, которые необходимо учитывать при расчетах.

Такими операциями являются :

Операция присваивание: а = b;

Одномерная индексация a[i] : (адрес (a)+i*длина элемента);

Арифметические операции: (* , / , - , +);

Операции сравнения: a < b;

Логические операции {or, and, not} ;

Конструкция «Следование» Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом, где k – количество блоков.

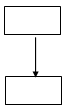
Конструкция «Ветвление»

If( условие) then (блок с трудоемкостью fthen и вероятностью p)

else (блок с трудоемкостью f_else и вероятностью (1-p)

Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «then» и «else» и определяется как:

К этому придется еще добавить трудоемкость вычисления условия.

Для анализа худшего случая выбирается тот блок ветвления, который имеет большую трудоемкость, а для лучшего – тот, трудоемкость которого минимальна.

Конструкция “Цикл”

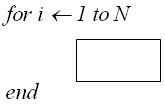
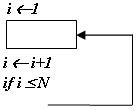
Общая трудоемкость определяется как

Примеры анализа трудоемкости алгоритмов.

Пример 1 Задача суммирования элементов квадратной матрицы

SumM (A, n; Sum)

Sum =0 // 1 операция

For i = 1 to n // 3 операции на один проход цикла

For j = 1 to n // 3 операции на один проход цикла

Sum =Sum + A[i,j] // 4 операции

End for j

End for i

Return (Sum)

End.

Алгоритм выполняет одинаковое количество операций при фиксированном значении n, и, следовательно, является количественно-зависимым. Его функция трудоемкости зависит только от размерности конкретного входа. Применение методики анализа конструкции «Цикл » дает:

f_A(n)=1+1+ n *(3+1+ n *(3+4))=7*n²+4* n +2 = (n²) ,

где внутренний цикл : f₁(n) = 1+3*n+4*n

внешний цикл : f₂(n)= 1+3*n+n*f₁(n)

замечание по задаче:

под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается n² значений.

Общее замечание:

Количественно-зависимые по трудоемкости алгоритмы - это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:

Fa(n), n=f(N)

К ним можно отнести алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т .д.

Пример 2 Задача поиска максимума в массиве

MaxS (S,n; Max)

Max = S[1] // 2 операции

For i = 2 to n // 3 операции на один проход цикла

if Max < S[i] // 2 операции

then Max =S[i] // 2 операции

end for

return Max

End

Данный алгоритм является количественно-параметрическим.

Трудоемкость таких алгоритмов определяется количеством данных на входе и значениями этих данных:

Fa(n), n=f(N,р1…,рi)

В данном конкретном случае трудоемкость зависит от размера входа и от порядка расположения однородных элементов. Зависимость от значений не может быть полностью исключена, но она не является существенной, поэтому для фиксированной размерности исходных данных необходимо проводить анализ для худшего, лучшего и среднего случая. Примерами такого класса могут служить алгоритмы сортировки сравнениями, алгоритмы поиска минимума и максимума в массиве.

А). Худший случай

Максимальное количество переприсваиваний максимума (на каждом проходе цикла) будет в том случае, если элементы массива отсортированы по возрастанию. Трудоемкость алгоритма в этом случае равна:

f_A(n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 = (n).

Б) Лучший случай

Минимальное количество переприсваивания максимума (ни одного на каждом проходе цикла) будет в том случае, если максимальный элемент расположен на первом месте в массиве. Трудоемкость алгоритма в этом случае равна:

f_A(n)=1+1+1+ (n-1) (3+2)=5 n - 2 = (n).

В) Средний случай

Алгоритм поиска максимума последовательно перебирает элементы массива, сравнивая текущий элемент массива с текущим значением максимума. На очередном шаге, когда просматривается к-ый элемент массива, переприсваивание максимума произойдет, если в подмассиве из первых “к” элементов максимальным элементом является последний. Очевидно, что в случае равномерного распределения исходных данных, вероятность того, что максимальный из к элементов расположен в определенной (последней) позиции равна 1/к. Тогда в массиве из n элементов общее количество операций переприсваивания максимума определяется как:

-постоянная Эйлера

Величина Hn называется n-ым гармоническим числом. Таким образом, точное значение (математическое ожидание) среднего количества операций присваивания в алгоритме поиска максимума в массиве из n элементов определяется величиной Hn (при очень большом количестве испытаний)), тогда:

f_A(n)=1 + (n-1) (3+2) + 2 (ln (n) + )=5 n +2 ln(n) - 4 +2 = (n).

(В сущности это есть математическое ожидание среднего количества операций присваивания в алгоритме поиска максимума в массиве их n элементов. При этом мы предполагаем, что значения элементов распределены равномерно)

[Анализ сложности рекурсивных алгоритмов будет разобран на практике №3-4 для задачи вычисления факториала для некоторого значения n ( n – параметр алгоритма, а не количество слов на входе)]