
- •2. Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным
- •3. Классификация эконометрических моделей
- •4. Оценка точности и качества прогнозов
- •5. Этапы эконометрического моделирования. Проблемы, решаемые при эконометрическом исследовании
- •6. Доверительные интервалы прогноза
- •8. Классификация видов эконометрических переменных и типов данных.
- •9. Регрессионный анализ
- •11. Показатели вариации
- •12. Критерий Дарбина — Уотсона
- •13. Соизмеримые показатели тесноты связи
- •14. Тесты на наличие автокорреляции.
- •16. Устранение автокорреляции.
- •17. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
- •18. Коэффициент эластичности.
- •19. Коэффициенты для моделей множественной регрессии
- •20. Коэффициент ранговой корреляции Спирмена
- •21. Коэффициент множественной корреляции
- •22. Гетероскедастичность модели регрессии
- •23. Множественный коэффициент детерминации
- •24. Парный регрессионный анализ
- •26. Производственные функции
- •27. Временные ряды и прогнозирование
- •28. Аналитический вид тренда
- •30. Метод экстрополяции
- •32. Множественная регрессия
- •33. Метод интерполяции
- •34. Коэффициент контингенции
- •35.Среднее квадратическое отклонение, дисперсия.
- •36. Точечный и интервальный прогноз для модели парной регрессии
- •37. Компоненты временного ряда
- •38.Модели регрессии с точками разрыва
- •39. Методы фильтрации временного ряда
- •40. Гомоскедастичность и гетероскедастичность остатков модели регресиии.
21. Коэффициент множественной корреляции
Множественный коэффициент корреляции R (множественное R) - это положительный квадратный корень из R-квадрата (множественного коэффициента детерминации, см. Остаточная дисперсия и коэффициент детерминации R-квадрат). Эта статистика полезна при проведении многомерной регрессии (т.е. использовании нескольких независимых переменных), когда необходимо описать зависимость между переменными.
Множественный коэффициент корреляции характеризует тесноту связи между зависимой переменной и предиктором. Он изменяется в пределах от 0 до 1 и рассчитывается по формуле:
![]()
где - определитель корреляционной матрицы;
- алгебраическое дополнение -го элемента.
Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. Гипотеза о его значимости отвергается, если значение вероятности отклонения превышает заданный уровень (чаще всего берут = 0.1, 0.05; 0.01 или 0.001).
Наблюдаемое значение находится по формуле:
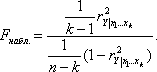
При небольшом числе наблюдений величина множественного коэффициента корреляции, как правило, завышается.
Множественный коэффициент корреляции считается значительным, т.е. имеет место статистическая зависимость между и остальными факторами , если где определяется по таблице F-распределения.
Функциональная связь возникает при значении равном 1, а отсутствие связи - 0. На долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
Множественное R применяется во многих модулях STATISTICA, например: Множественная регрессия, Общие линейные модели (GLM), Общие регрессионные модели (GRM) и Планирование и анализ эксперимента.
22. Гетероскедастичность модели регрессии
лучайной ошибкой называется отклонение в линейной модели множественной регрессии:
εi=yi–β0–β1x1i–…–βmxmi
В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:
![]()
где ei – остатки модели регрессии.
Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.
При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:
6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
![]()
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
![]()
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
![]()
Второе условие
![]()
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.
Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.
Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.
Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
![]()
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:

Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:
εi~N(0; G2Ω),
где Ω – матрица ковариаций случайной ошибки.
Если дисперсии случайных ошибок
![]()
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить.
Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
![]()
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
![]()
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:
1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;
2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.
