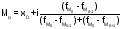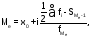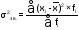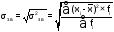Методичні рекомендації
Основні формули для розрахунку характеристик рядів розподілу наведено в табл.1.
Табл.1
|
мода |
|
|
медіана |
|
|
дисперсія |
|
|
середнє квадратичне відхилення |
|
|
коефіцієнт варіації |
|
Вирішення задач аналізу рядів розподілу типу в табличному процесорі Excel можна завдяки використання програмної надбудови Пакет аналізу й убудованих статистичних функцій. Розглянемо порядок роботи в Excel.
Згідно отриманих даних: коефіцієнт осциляції
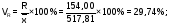
коефіцієнт
варіації
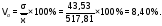
На прикладі розглянемо дані по областям за кількість прибувши в Україну які представлені в табл.2
табл.2
|
У межах України | |
|
області |
кількість прибулих |
|
Вінницька |
28037 |
|
Волинська |
15544 |
|
Дніпропетровська |
42680 |
|
Донецька |
47682 |
|
Житомирська |
20461 |
|
Закарпатська |
6561 |
|
Запорізька |
20655 |
|
Івано-Франківська |
15906 |
|
Київська |
35533 |
|
Кіровоградська |
15043 |
|
Луганська |
26934 |
|
Львівська |
29077 |
|
Миколаївська |
13866 |
|
Одеська |
32019 |
|
Полтавська |
23585 |
|
Рівненська |
18332 |
|
Сумська |
17768 |
|
Тернопільська |
12714 |
|
Харківська |
41731 |
|
Херсонська |
12538 |
|
Хмельницька |
21709 |
|
Черкаська |
18964 |
|
Чернівецька |
10914 |
|
Чернігівська |
14578 |
Режим Описова статистика служить для генерації одномірного статистичного звіту по основним показникам положення, розсіювання й асиметрії сукупності, що аналізується. Для переходу в цій режим необхідно ввійти в позицію меню Сервіс – Аналіз даних й обрати даний режим 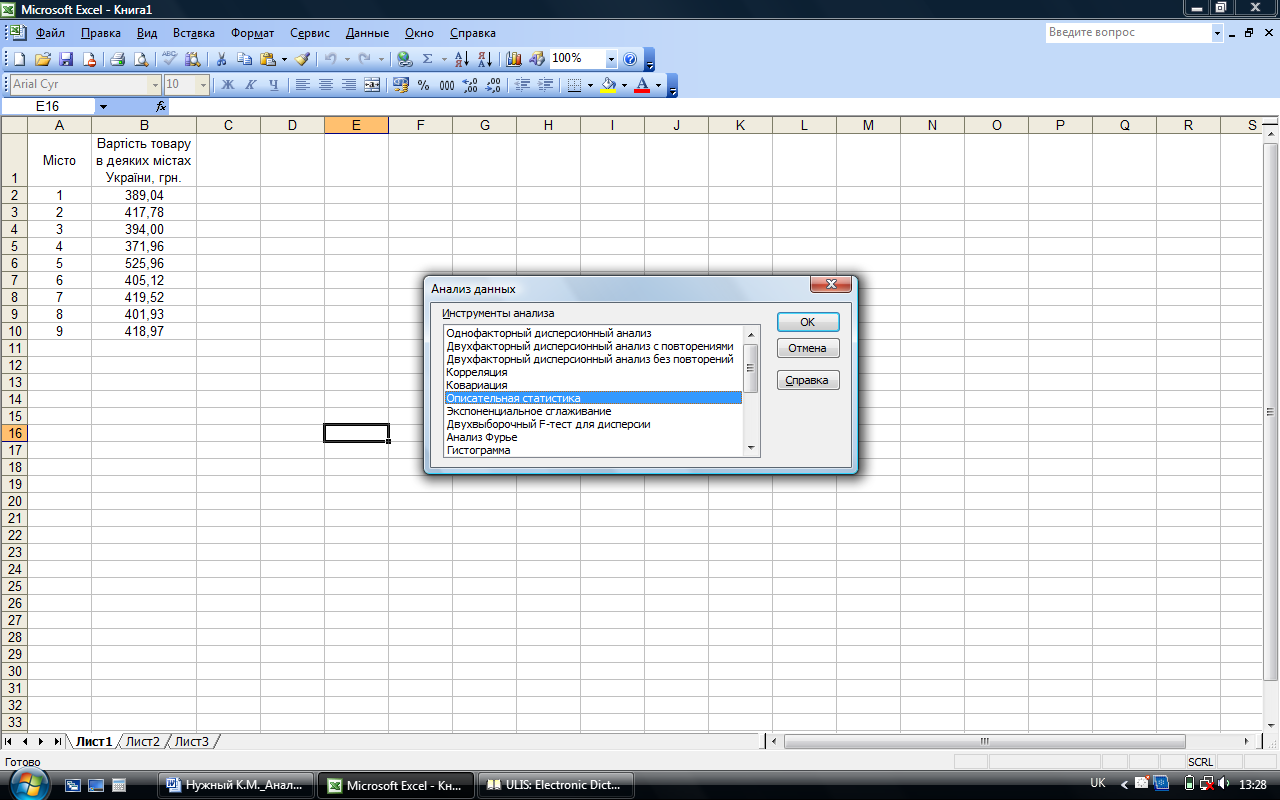(рис. 1).
рис.1
В діалоговому вікні даного режиму (рис.2) задаються наступні параметри.
Введені параметри режиму Описова статистика представлені на рис.2, а розраховані показники в даному режимі – рис. 3.
Рис.2. Значення параметрів режиму Описова статистика
|
Столбец1 | ||
|
|
|
|
|
Среднее |
|
22617,95833 |
|
Стандартная ошибка |
|
2209,421879 |
|
Медиана |
|
19712,5 |
|
Мода |
|
#Н/Д |
|
Стандартное отклонение |
|
10823,91246 |
|
Дисперсия выборки |
|
117157081 |
|
Эксцесс |
|
0,07332652 |
|
Асимметричность |
|
0,898324685 |
|
Интервал |
|
41121 |
|
Минимум |
|
6561 |
|
Максимум |
|
47682 |
|
Сумма |
|
542831 |
|
Счет |
|
24 |
|
Наибольший(1) |
|
47682 |
|
Наименьший(1) |
|
6561 |
|
Уровень надежности(95,0%) |
|
4570,53736 |
Рис. 3. Розраховані показники описової статистики
Згідно отриманих даних:
|
коефіцієнт осциляції |
1,818068607 |
|
коефіцієнт варіації |
0,478553913 |
Аналіз згрупованих статистичних даних. Після вводу або перенесення з документів Microsoft Office через буфер обміну вхідних даних в таблицю Excel, якщо потрібно, відбувається перетворення та візуалізація первинних даних. В даному випадку, необхідно додати стовбець з індивідуальними значеннями усереднюваної ознаки (середину інтервалу) по кожній групі (рис.4).
В явному виді функція для розрахунку середньої арифметичної зваженої (2) не представлена в Excel. Але її можливо отримати комбінацією інших функцій.
|
вихідні дані |
розрахункові дані | |
|
интервал |
кількість |
|
|
до 0,1 |
1 |
0,9 |
|
0,1-37,025 |
14 |
18,5625 |
|
37,025-73,95 |
5 |
55,4875 |
|
73,75 -110,875 |
1 |
92,4125 |
|
більше 110,875 |
2 |
111,875 |
|
середня сума |
12,14076087 | |
Рис. 4. Розрахунок середньої суми оборотних активів
Для визначення моди (3) й медіани (4) необхідно провести деякі розрахунки (рис. 5-6).
Розрахунок моди ряду представлено на рис. 5.
|
вихідні дані |
розрахункові дані | |
|
интервал |
кількість |
|
|
до 0,1 |
1 |
0,9 |
|
0,1-37,025 |
14 |
18,5625 |
|
37,025-73,95 |
5 |
55,4875 |
|
73,75 -110,875 |
1 |
92,4125 |
|
більше 110,875 |
2 |
111,875 |
|
модальна кількість |
14 | |
|
зміщення в стовбці на модальне значення |
2 | |
|
модальний інтервал |
0,1-37,025 | |
|
нижня границя модального інтервалу |
0,1 | |
|
кількість областей, що мають меншу чисельність прибулих |
1 | |
|
кількість областей, що мають більшу численність прибулих |
5 | |
|
мода суми оборотних активів |
1,281818182 | |
Рис. 5. Розрахунок моди ряду
У зв’язку з тим, що медіана ділить чисельність ряду навпіл, то вона буде там, де накопичена частота складає половину або більше половини всій суми частот, а попередня накопичена частота менше половини чисельності сукупності (рис. 6).
|
вихідні дані |
розрахункові дані | |
|
интервал |
кількість |
накопичена частота |
|
до 0,1 |
1 |
1 |
|
0,1-37,025 |
14 |
15 |
|
37,025-73,95 |
5 |
20 |
|
73,75 -110,875 |
1 |
21 |
|
більше 110,875 |
2 |
23 |
|
всього |
23 |
|
|
50 % кількості |
11,5 | |
|
зміщення на max ≤ N/2 |
1 | |
|
значення max ≤ N/2 |
1 | |
|
зміщення на медіанний інтервал |
2 | |
|
частота медіанного інтервалу |
15 | |
|
медіанний інтервал |
0,1-37,025 | |
|
нижня границя медіанного інтервалу |
0,1 | |
|
значення накопиченої частоти попереднього інтервалу |
1 | |
|
медіана суми оборотних активів |
1,5 | |
Рис. 6. Розрахунок медіани ряду
Розрахунок середнього квадратичного відхилення дозволило визначити коефіцієнт варіації (рис. 7).
|
вихідні дані |
розрахункові дані | |
|
интервал |
кількість |
накопичена частота |
|
до 0,1 |
1 |
0,9 |
|
0,1-37,025 |
14 |
18,5625 |
|
37,025-73,95 |
5 |
55,4875 |
|
73,75 -110,875 |
1 |
92,4125 |
|
більше 110,875 |
2 |
111,875 |
|
Середня кількість прибулих |
37,14673913 | |
|
Дисперсія |
958,8656144 | |
|
Середнє квадратичне відхилення |
30,96555529 | |
|
коефіцієнт вариації |
83,36009032 | |
Рис.7. Розрахунок дисперсії, середнього квадратичного відхилення й коефіцієнта варіації
Для розрахунку квартильного показника варіації необхідно спочатку визначити верхній й нижній квартилі.
Обчислення першого квартиля (рис.8) виконується аналогічно розрахунку медіани, крім наступних клітинок:
Для першого квартиля кількість всього ми множимо на 0,25, а третього множимо на 0,75. Третій квартиль знаходиться в інтервалі 73,75-110,875
|
вихідні дані |
розрахункові дані | |||
|
интервал |
кількість |
накопичена частота | ||
|
до 0,1 |
1 |
1 | ||
|
0,1-37,025 |
14 |
15 | ||
|
37,025-73,95 |
5 |
20 | ||
|
73,75 -110,875 |
1 |
21 | ||
|
більше 110,875 |
2 |
23 | ||
|
всього |
23 |
| ||
|
25% числа областей |
5,75 |
17,25 | ||
|
зміщення на max ≤ N/2 |
1 | |||
|
значення max ≤ N/2 |
1 | |||
|
зміщення на перший квартальний інтервал |
2 | |||
|
Накопичена частота першого квартального інтервала |
15 | |||
|
Перший квартальнтальний інтервал |
0,1-37,025 | |||
|
Нижня грания першого квартального інтервала |
0,1 | |||
|
значення накопиченої частоти |
1 | |||
|
перший квартиль |
0,733333333 | |||
|
третій квартиль |
2,266666667 | |||
Рис. 8. Розрахунок першого квартиля
Результати розрахунку загальної дисперсії та її складових представлено на рис. 9
|
Області |
Промисловість |
Розрахункові дані | ||
|
добувна |
переробна | |||
|
Вінницька |
2510 |
1368 |
| |
|
Волинська |
1032 |
734 |
| |
|
Дніпропетровська |
3900 |
3093 |
| |
|
Донецька |
2144 |
3566 |
| |
|
Житомирська |
1222 |
1443 |
| |
|
Закарпатська |
1196 |
921 |
| |
|
Запорізька |
2719 |
1916 |
| |
|
Івано-Франківська |
930 |
1435 |
| |
|
Київська |
2239 |
2750 |
| |
|
Кіровоградська |
3103 |
895 |
| |
|
Луганська |
1504 |
1861 |
| |
|
Львівська |
1365 |
2844 |
| |
|
Миколаївська |
3624 |
1155 |
| |
|
Одеська |
4565 |
2297 |
| |
|
Полтавська |
2345 |
1236 |
| |
|
Рівненська |
772 |
906 |
| |
|
Сумська |
1104 |
870 |
| |
|
Тернопільська |
1214 |
919 |
| |
|
Харківська |
1963 |
3755 |
| |
|
Херсонська |
2542 |
964 |
| |
|
Хмельницька |
1504 |
1107 |
| |
|
Черкаська |
1962 |
1165 |
| |
|
Чернівецька |
735 |
598 |
| |
|
Чернігівська |
1277 |
881 |
| |
|
разом |
47471 |
38679 |
| |
|
Середній обєм виконаних робіт в промисловості двох форм |
8615 | |||
|
Середній обєм виконаних робіт в добувній промисловості |
9494,2 | |||
|
Середній обєм виконаних робіт в переробній промисловості |
7735,8 | |||
|
внутрішньо групова дисперсія (добувна) |
1024270,873 | |||
|
внутрішньо групова дисперсія (переробна) |
843295,0677 | |||
|
середня із внутрішньо груповіх диспесій |
933782,9705 | |||
|
міжгрупова дисперсія |
772992,64 | |||
|
загальна дисперсія |
1706775,61 | |||
Рис. 9. Розрахунок загальної дисперсії та її складових
Визначенні дисперсія та середнє квадратичне відхилення альтернативної ознаки представлено на рис.10.
|
Області |
|
Промисловість |
|
| |||
|
усього |
добувна |
переробна |
| ||||
|
Вінницька |
19135 |
2510 |
1368 |
| |||
|
Волинська |
13238 |
1032 |
734 |
| |||
|
Дніпропетровська |
42823 |
3900 |
3093 |
| |||
|
Донецька |
47389 |
2144 |
3566 |
| |||
|
Житомирська |
15560 |
1222 |
1443 |
| |||
|
Закарпатська |
14258 |
1196 |
921 |
| |||
|
Запорізька |
24898 |
2719 |
1916 |
| |||
|
Івано-Франківська |
16886 |
930 |
1435 |
| |||
|
Київська |
31534 |
2239 |
2750 |
| |||
|
Кіровоградська |
13936 |
3103 |
895 |
| |||
|
Луганська |
21618 |
1504 |
1861 |
| |||
|
Львівська |
35264 |
1365 |
2844 |
| |||
|
Миколаївська |
18848 |
3624 |
1155 |
| |||
|
Одеська |
37915 |
4565 |
2297 |
| |||
|
Полтавська |
19880 |
2345 |
1236 |
| |||
|
Рівненська |
12710 |
772 |
906 |
| |||
|
Сумська |
12684 |
1104 |
870 |
| |||
|
Тернопільська |
13349 |
1214 |
919 |
| |||
|
Харківська |
38228 |
1963 |
3755 |
| |||
|
Херсонська |
15363 |
2542 |
964 |
| |||
|
Хмельницька |
16546 |
1504 |
1107 |
| |||
|
Черкаська |
17101 |
1962 |
1165 |
| |||
|
Чернівецька |
9982 |
735 |
598 |
| |||
|
Чернігівська |
13039 |
1277 |
881 |
| |||
|
разом |
|
47471 |
38679 |
| |||
|
Середній відсоток в трьох промисловостях |
1,227306807 | ||||||
|
середній відсоток переробної промисловості |
-0,227306807 | ||||||
|
Дисперсія питомої ваги добувної промисловості (дисперсія альтернативної ознаки) |
-0,278975192 | ||||||
|
Середнє квадратичне відхилення альтернативної ознаки |
#ЧИСЛО! | ||||||
Рис.10. Розрахунок дисперсії та середнього квадратичного відхилення
Визначення коефіцієнтів асиметрії й ексцесу передбачає розрахунок моментів третього та четвертого порядку (рис.11).
|
интервал |
кількість |
накопичена частота |
|
до 0,1 |
1 |
0,9 |
|
0,1-37,025 |
14 |
18,5625 |
|
37,025-73,95 |
5 |
55,4875 |
|
73,75 -110,875 |
1 |
92,4125 |
|
більше 110,875 |
2 |
111,875 |
|
Середній |
37,14673913 | |
|
Дисперсія |
958,8656144 | |
|
Середнє квадратичне відхилення |
30,96555529 | |
|
момент третього порядку |
23401,4589 | |
|
коефіцієнт асиметрії |
0,788145347 | |
|
момент четвертого порядку |
3289554,359 | |
|
коефіцієнт ексцесу |
0,577845459 | |
Рис. 1. Розрахунок коефіцієнтів асиметрії та ексцесу