Задача 4.1

В течение девяти последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной рядY(t) этого показателя приведен ниже в таблице.

t	1	2	3	4	5	6	7	8	9
Yt	10	14	21	24	33	41	44	47	49

Требуется:

1. Проверить наличие аномальных наблюдений.

2. Построить линейную модель Ŷ(t) =a₀+a₁t, параметры которой оценить МНК (Ŷ(t) – расчетные, смоделированные значения временного ряда.).

3. Построить адаптированную модель Брауна Ŷ(t) =a₀+a₁kс параметром сглаживания α = 0,4 и α = 0,7; выбрать лучшее значение параметра сглаживания.

4. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использования R/S-критерия взять табулированные границы 2,7 – 3,7).

5. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.

6. По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности p= 70 %).

7. Фактические значения показателя, результаты моделирования и прогнозирования представить графически.

Решение:

1.Проверим наличие аномальных наблюдений с помощью метода Ирвина. Для этого надо вычислить величину λ_tпо формуле λ_t=y_t–y_расч/S_y,

_______________

где S_y= √(y_t–y_ср)²/(n– 1).

Если рассчитанная величина λ_tпревышает табличный уровень, то уровеньy_tсчитается аномальным. Для десяти наблюдений λ_табл= 1,5. Согласно колонке 15 таблицы 5 аномальных наблюдений нет.

2. Уравнение линейной регрессии имеет вид: y_расч=a₀+a₁∙t. Значения параметровa₀иa₁линейной модели определим, используя данные таблицы 1.

Таблица 1.

	t	Yt	t∙Yt	t2
	1	10	10	1
	2	14	28	4
	3	21	63	9
	4	24	96	16
	5	33	165	25
	6	41	246	36
	7	44	308	49
	8	47	376	64
	9	49	441	81
Сумма	45	283	1733	285
Среднее	5	31,4	193	31,7

(y∙t)_ср–y_ср∙t_ср193 – 131,4 ∙ 5

a₁ = ——————— = —————–– = 4,9

(t²)_ср – (t_ср)² 31,7 – 5

a₀ = y_ср – a₁ ∙ t_ср = 31,4 – 5 ∙ 5 = 5,3

Уравнение линейной регрессии имеет вид: y_расч= 5,30 + 4,94 ∙t.

3. Построим адаптивную модель Брауна.

n	1	2	3	4	5	6	7	8	9
x	10	14	21	24	33	41	44	47	49

Начальные оценки параметров получим по первым пяти точка при помощи метода наименьших квадратов.

na₀ + a₁∑x = ∑y

a₀∑x + a₁∑x² = ∑xy

5a₀ + 15a₁ = 102

15a₀ + 55a₁ = 362

∑y ∙ ∑x² – ∑xy ∙ ∑x

a₀ = —————————

n ∑x² - ∑x ∙ ∑x

102 ∙ 55 – 362 ∙ 15

a₀ = —————————— ≈ 3,60

5 ∙ 55 – 15 ∙ 15

n∑xy– ∑y ∙ ∑x

a₁ = ———————

n∑x²– ∑x∙ ∑x

5 ∙ 362 – 102 ∙ 15

a₁= —————————— ≈ 5,60

5 ∙ 55 – 15 ∙ 15

Данные для расчета возьмем в следующей таблице:

						Сумма
x	1	2	3	4	5	15
y	10	14	21	24	33	102
x2	1	4	9	16	25	55
xy	10	28	63	96	165	362

Уравнение линейной регрессии имеет вид: y_x= 3,60 + 5,60x.

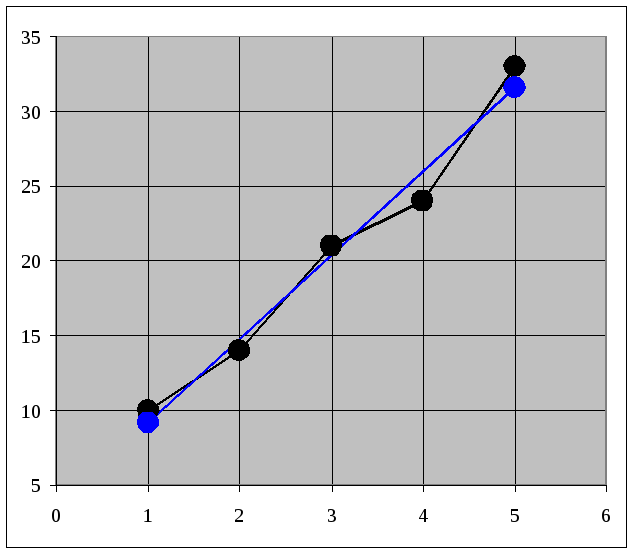
Получили a₀(0) = 3,60,a₁(0) = 5,60.

Возьмем α = 0,4, k= 1 и β = 1 – α = 1 – 0,4 = 0,6.

Будем находить последующие значения a₀(t) иa₁(t) по формулам

a₁(t) = a₁(t – 1) + (1 – β)² ∙ (Y(t) – Y_p(t)) и a₀(t) = a₀(t – 1) + a₁(t – 1) + (Y(t) – Y_p(t)) ∙ (1 – β²),

где Y_p(t) = a₀(t – 1) + a₁(t – 1)k.

Номер	Факт	a0	a1	Расчет	Отклонение
		3,60	5,60
1	10	9,71	5,73	9,20	0,800
2	14	14,52	5,50	15,44	-1,440
3	21	20,65	5,66	20,02	0,984
4	24	24,83	5,29	26,30	-2,301
5	33	31,96	5,75	30,12	2,885
6	41	39,82	6,27	37,71	3,290
7	44	44,75	5,94	46,09	-2,090
8	47	48,33	5,35	50,69	-3,693
9	49	50,68	4,60	53,68	-4,679
10				55,29
11				59,89

___________________

u(1) = 1,12 ∙ 3,12 ∙ √1 + 1/9 + (9 + 1 – 5)²/60 ≈ 4,32

k= 1 (t= 10).

Нижняя граница: 55,29 – 4,32 = 50,97

Верхняя граница: 55,29 + 4,32 = 59,60

___________________

u(2) = 1,12 ∙ 3,12 ∙ √1 + 1/9 + (9 + 2 – 5)²/60 ≈ 4,57

k= 2 (t= 10).

Нижняя граница: 59,89 – 4,57 = 55,32

Верхняя граница: 59,89 + 4,57 = 64,45

Результаты аппроксимации и прогнозирования по адаптивной модели Брауна при α = 0,4.

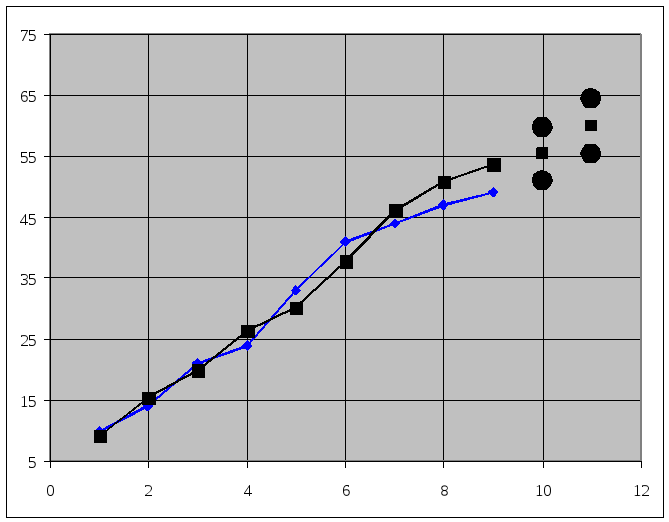
Возьмем α = 0,7, k= 1 и β = 1 – α = 1 – 0,7 = 0,3.

Будем находить последующие значения a₀(t) иa₁(t) по формулам

a₁(t) = a₁(t – 1) + (1 – β)² ∙ (Y(t) – Y_p(t)) и a₀(t) = a₀(t – 1) + a₁(t – 1) + (Y(t) – Y_p(t)) ∙ (1 – β²),

где Y_p(t) = a₀(t – 1) + a₁(t – 1)k.

Номер	Факт	a0	a1	Расчет	Отклонение
		3,60	5,60
1	10	9,93	5,99	9,20	0,800
2	14	14,17	5,05	15,92	-1,920
3	21	20,84	5,92	19,22	1,776
4	24	24,25	4,57	26,76	-2,762
5	33	32,62	6,62	28,82	4,183
6	41	40,84	7,48	39,24	1,758
7	44	44,39	5,36	48,32	-4,321
8	47	47,25	4,01	49,75	-2,751
9	49	49,20	2,91	51,26	-2,262
10				52,11
11				55,02

___________________

u(1) = 1,12 ∙ 3,10 ∙ √1 + 1/9 + (9 + 1 – 5)²/60 ≈ 4,28

k= 1 (t= 11).

Нижняя граница: 52,11 – 4,28 = 47,82

Верхняя граница: 52,11 + 4,28 = 56,39

___________________

u(2) = 1,12 ∙ 3,10 ∙ √1 + 1/9 + (9 + 2 – 5)²/60 ≈ 4,57

k= 2 (t= 11).

Нижняя граница: 55,02 – 4,53 = 50,48

Верхняя граница: 55,02 + 4,53 = 59,55

Результаты аппроксимации и прогнозирования по адаптивной модели Брауна при α = 0,7.

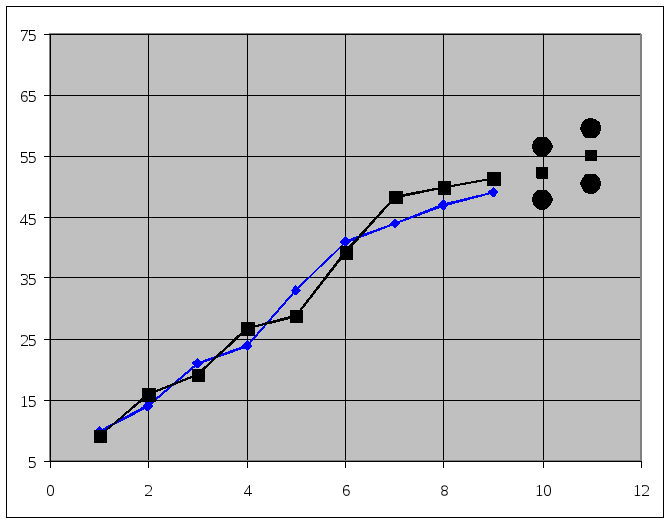
Очевидно, что лучше взять α = 0,7.

4. Для того чтобы оценить параметры и качество этой модели (адекватность), а также построить точечный и интервальный прогнозы, заполним следующую таблицу:

Таблица 5.

t	Yt	t-tср	(t-tср)2	Yt-yср	(t-tср)(Yt-yср)	Yt*	εt= Yt- Yt*	Точ. пов	εt2	εt-εt-1	(εt-εt-1)2	εt∙εt-1	(εt- εср)2	λt
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	10	-4	16	-21,44	85,78	10,24	-0,24	-	0,0576				0,060	0,1
2	14	-3	9	-17,44	52,33	15,54	-1,54	1	2,3716	-1,3	1,69	0,3696	2,385	0,7
3	21	-2	4	-10,44	20,89	20,84	0,16	1	0,0256	1,7	2,89	-0,246	0,024	0,1
4	24	-1	1	-7,44	7,44	26,14	-2,14	1	4,5796	-2,3	5,29	-0,342	4,599	0,9
5	33	0	0	1,56	0,00	31,44	1,56	0	2,4336	3,7	13,69	-3,338	2,420	0,7
6	41	1	1	9,56	9,56	36,74	4,26	1	18,1476	2,7	7,29	6,6456	18,110	1,8
7	44	2	4	12,56	25,11	42,04	1,96	0	3,8416	-2,3	5,29	8,3496	3,824	0,8
8	47	3	9	15,56	46,67	47,34	-0,34	0	0,1156	-2,3	5,29	-0,666	0,119	0,1
9	49	4	16	17,56	70,22	52,64	-3,64	1	13,2496	-3,3	10,89	1,2376	13,282	1,5
45	283	0	60	0	318	282,96	0,04	5	44,8224		52,32	12,01	44,822
5	31,4

В первой нижней строке под таблицей записаны суммы соответствующих граф, во второй – соответствующие средние значения.

Наличие тренда, то есть меру связи между переменными tиY_tоценим по коэффициенту корреляции. Построим вспомогательную расчетную таблицу:

	t	Yt	t-tср	(t-tср)2	Yt-Yср	(Yt-Yср)2	t∙Yt
	1	10	-4	16	-21,44	459,86	10
	2	14	-3	9	-17,44	304,31	28
	3	21	-2	4	-10,44	109,09	63
	4	24	-1	1	-7,44	55,42	96
	5	33	0	0	1,56	2,42	165
	6	41	1	1	9,56	91,31	246
	7	44	2	4	12,56	157,64	308
	8	47	3	9	15,56	241,98	376
	9	49	4	16	17,56	308,20	441
Сумма	45	283	0	60	0	1730,22	1733
Среднее	5	31,4	0	6,67	0	192,25	192,56

Коэффициент корреляции:

____ _ __

t ∙ Y_t – t ∙ Y_t

r = ————

_t ∙ _y

где _t² = ∑(t – t_ср)²/n

_y² = ∑( Y_t – Y_ср)²/n

t_ср= ∑t/n

Y_tср= ∑Y_t/n

t_ср= 45/9 = 5

Y_tср= 283/9 = 31,4

_t² = 60/9 = 6,67

_y² = 1730,22/9 = 192,25

r= (192,56 – 5 ∙ 31,4)/(2,58 ∙ 13,87) = 0,99

Оценим полученный коэффициент корреляции по статистике Стьюдента. То есть проверим гипотезу о ненулевом коэффициенте корреляции генеральной совокупности. Для проверки гипотезы установим значения t_иF_и сравним с заданными табличными значениями.

r²(n– 2) 0,99²(9 – 2)

t_= ———— = ————— = 263,21

1 – r²1 – 0,99²

Для уровня значимости = 0,05 при числе степеней свободыm=9t_табл= 2,262. Так какt_>t_табл, то гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности отвергаем.

Для проверки адекватности модели в соответствии и видом формул

|ε_ср| _ ∑(ε_t– ε_t-1)²

ť = —— ∙ √nd= —————r₁= (∑ε_t∙ε_t-1) : ∑ ε_t².

S_∑∑ ε_t²

организуем заполнение граф 9 – 13.

• Легко убедиться, что математическое ожидание ряда остатков равна нулю, т.е. |ε_ср| = 0.

• Проверка случайности ряда остатков по критерию пиков дает результат: 5 (сумма графы 9) больше 0 (критическое число поворотных точек).

__________ _____

/ ∑ (ε_t– ε_ср)²/ 44,82

S_∑= / ————— = / ——— = 2,37

√ n– 1 √ 8

|ε_ср| _ 0,04 _

ť = —— ∙ √n= —— ∙ √9 = 0,05

S_∑2,37

• Вычислим d по формуле

∑(ε_t– ε_t-1)²52,32

d= ————— = ——— = 1,17

∑ ε_t²44,82

При проверке независимости уровней ряда остатков друг от друга значение d= 1,17 при уровне значимостиa= 0,025 попадает в интервал междуd₁= 1,08 иd₂= 1,36, т.е. в область неопределенности. Поэтому придется воспользоваться формулой

r₁= (∑ε_t∙ε_t-1) / ∑ ε_t²= 12,01/44,82 = 0,27.

Сопоставляя это число с табличным значением первого коэффициента автокорреляции 0,36, взятым для уровня значимости a= 0,01 иn= 9, увидим, что расчетное значение меньше табличного. Это означает, что с ошибкой в 1% ряд остатков можно считать некоррелированным, т.е. свойство взаимной независимости уровней остаточной компоненты подтверждается.

• Соответствие ряда остатков нормальному распределению установим с помощью формулы

R/S = (ε_max – ε_min)/S_,

_______________ ______

S_ = √ ∑(ε_t - ε_ср)²/(n – 1) = √ 44,82/8 = 2,37

R/S = (4,26 – (-3,64))/S_ = 3,34

Дляn= 9 иa= 0,05 найдем критический интервал: [2,7; 3,7]. Вычисленное значение 3,34 попадает между табулированными границами с заданным уровнем вероятности. Значит, закон нормального распределения выполняется, и можно строить доверительный интервал прогноза.

5. Так как модель оказалась адекватной, оценим ее точность. Рассчитаем среднюю относительную ошибку по формуле

1 |ε_t| 1

E_отн= — ∑ —— ∙ 100% = — ∙ 0,51 ∙ 100% = 5,6 %.

n|Y_t| 9

Такую ошибку можно считать приемлемой.

6. Экстраполяция уравнения Y_t* = 4,94 + 5,30tвперед дает прогнозное значение равноеY₁₀= 57,94 и равноеY₁₁= 63,24.

Для построения интервального прогноза рассчитаем доверительный интервал. Примем значение уровня значимости a= 0,3, а значит, доверительную вероятность – 70 %. В этом случае критерий Стьюдента (при=n– 2 = 7) равенt_,= 1,12. Вычислив среднеквадратическую ошибку тренда, с учетом значенияt_,получим интервальный прогноз:

____________________

u(1) = 1,12 ∙ 2,53 ∙ √1 + 1/9 + (9 + 1 – 5)²/60 ≈ 3,50

k= 1 (t= 10).

Нижняя граница: 55,29 – 3,50 = 54,44

Верхняя граница: 55,29 + 3,50 = 61,45

___________________

u(2) = 1,12 ∙ 2,53 ∙ √1 + 1/9 + (9 + 2 – 5)²/60 ≈ 3,71

k= 2 (t= 10).

Нижняя граница: 63,24 – 3,71 = 59,54

Верхняя граница: 63,24 + 43,71 = 66,95

Таким образом, построенная модель является полностью адекватной динамике фактических показателей. Поэтому с вероятностью 70 % можно утверждать, что при сохранении сложившихся закономерностей развития значение показателя, прогнозируемое на 10 и 11 наблюдения с помощью линейной модели роста, попадают в промежуток, образованный нижней и верхней границей доверительного интервала.

7. Представим графически фактические значения показателя, результаты моделирования и прогнозирования.

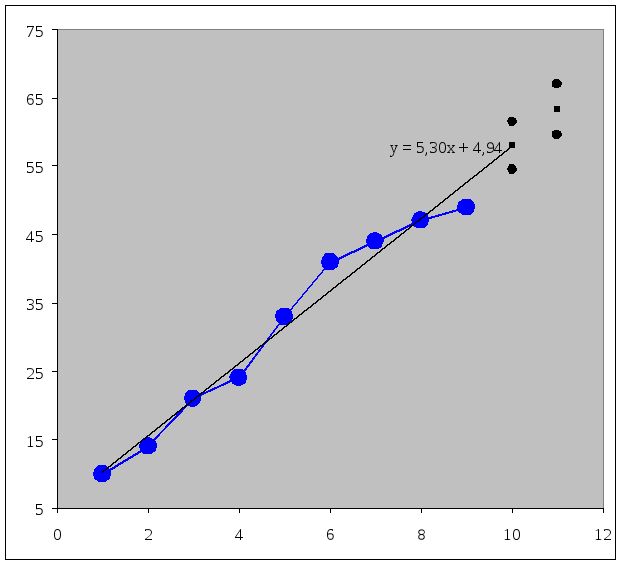
Данная работа скачена с сайта Банк рефератов http://www.vzfeiinfo.ru. ID работы: 25568

15