Задача 1.5. Прогнозирование среднего значения

5. Для выбранной модели осуществите прогнозирование среднего значения показателя Y при уровне значимости α=0.1, если прогнозное значение фактора Х составит 80% от его максимального значения. Представьте графически: фактические и модельные значения Y, точки прогноза прогнозирования.

Согласно условию задачи прогнозное значение фактора Х₄ составляет 80% от его максимального значения. Максимальное значение Х₄=91 найдем с помощью функции МАКС в Excel. Тогда прогнозное значение Х₄^*=72.8. Рассчитаем по уравнению модели (1): прогнозное значениеY:

Таким образом, если жилая площадь квартиры составит 80% от ее максимального значения и составит 72.8 кв. м, то ожидаемая цена квартиры будет составлять около 177,3878 тыс. долл.

Зададим доверительную вероятность p=1–α=1–0.1=0.9 и построим доверительный прогнозный интервал для среднего значения Y.

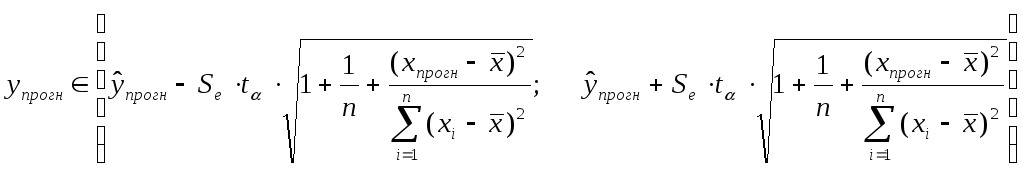
Предварительно подготовим:

• стандартная ошибка 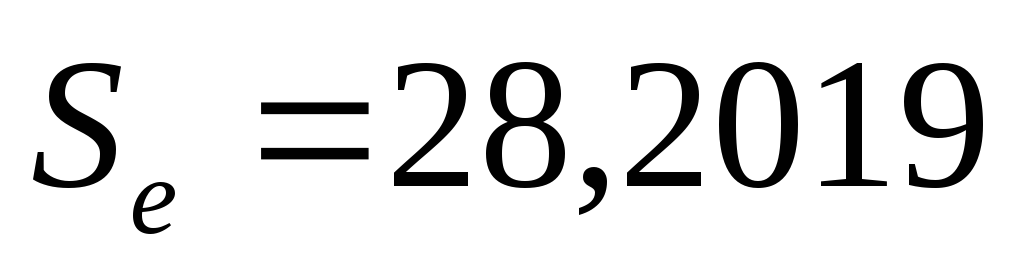(таблица «Регрессионная статистика» итогов применения инструмента «Регрессия» пакета «Анализ данных»);

• по столбцу данных Х₄ найдем среднее значение 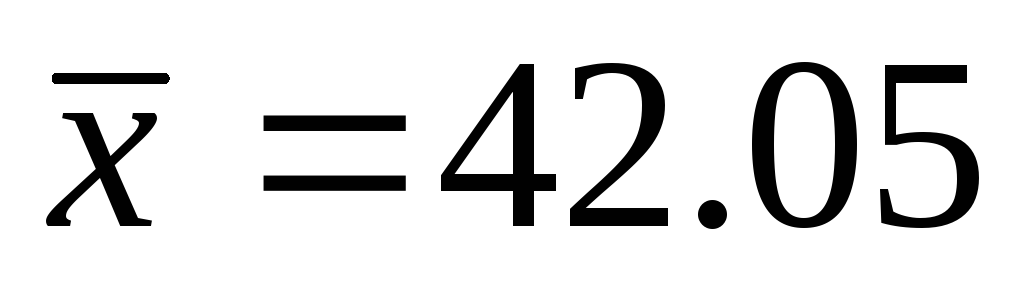(функция СРЗНАЧ) и определим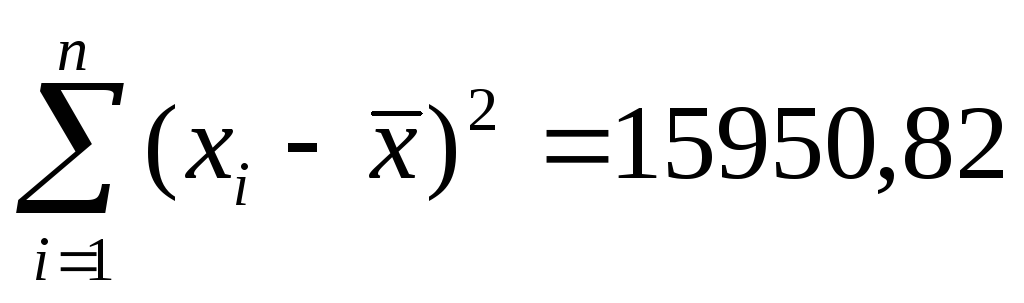(функция КВАДРОТКЛ);

• t_α – коэффициент Стьюдента для уровня значимости α=10% и числа степеней свободы k=38. t_α=1.686 (функция СТЬЮДРАСПОБР).

Тогда, предельная ошибка прогноза:

Следовательно, доверительный интервал имеет вид:

, т.е.

Таким образом, с надежностью 90% можно утверждать, что если жилая площадь квартиры составит 80% от ее максимального значения и составит 72,8 кв. м, то ожидаемая средняя цена квартиры будет от 127.8758 тыс. долл. до 226.8998 тыс. долл.

Выполненный прогноз стоимости квартиры оказался надежным (p=1–α=1–0.1=0.9), но не точным, так как диапазон верхней и нижней границ доверительного интервала отличаются в 1,77 раза:

D_Y = 226.8998 / 127.8758 = 1.77.

Для построения графика используем «Мастер диаграмм» – покажем фактические исходные данные (поле корреляции). Затем с помощью опции «Добавить линию тренда», построим линию модели и покажем на графике результаты прогнозирования.

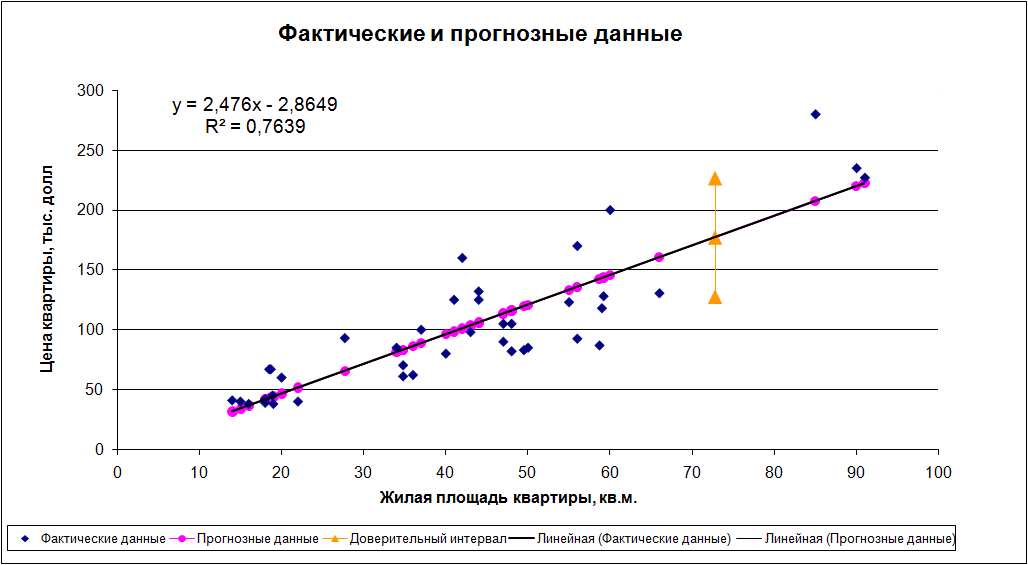
Задача 1.6. Пошаговая множественная регрессия

6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счет значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии.

Методом включения построим двухфакторные модели, сохраняя в них наиболее информативный фактор – жилую площадь квартиры (Х₄).

В качестве «входного интервала Х» укажем значения факторов Х₄ и Х₁, с помощью инструмента «Регрессия» получим:

Регрессионная статистика
Множественный R	0,875979141
R-квадрат	0,767339455
Нормированный R-квадрат	0,754763209
Стандартная ошибка	28,37139894
Наблюдения	40

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	98226,3515	49113,17573	61,01499	1,92E-12
Остаток	37	29782,6423	804,9362779
Итого	39	128008,994
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-6,436101071	11,5164888	-0,55885966	0,579624	-29,7707	16,89852	-29,7707	16,89852
X4	2,48928005	0,22535976	11,04580516	2,85E-13	2,032658	2,945902	2,032658	2,945902
X1	6,692936402	9,04586863	0,739888746	0,464037	-11,6357	25,02161	-11,6357	25,02161

Таким образом, модель (4) зависимости цены квартиры Y от жилой площади квартиры Х₄ и города области Х₁ построена, ее уравнение имеет вид:

Используем в качестве «входного интервала Х» значения факторов Х₄ и Х₂, с помощью «Регрессии» найдем:

Регрессионная статистика
Множественный R	0,874162592
R-квадрат	0,764160238
Нормированный R-квадрат	0,751412142
Стандартная ошибка	28,56458338
Наблюдения	40

Дисперсионный анализ
	df		SS		MS		F		Значимость F
Регрессия	2		97819,38		48909,69		59,94309		2,47E-12
Остаток	37		30189,61		815,9354
Итого	39		128009
	Коэффициенты		Стандартная ошибка		t-статистика		P-Значение		Нижние 95%		Верхние 95%		Нижние 95,0%		Верхние 95,0%
Y-пересечение	-2,167574535		11,07267		-0,19576		0,84587		-24,6029		20,26778		-24,6029		20,26778
X4	2,556497296		0,456314		5,602491		2,17E-06		1,631917		3,481078		1,631917		3,481078
X2	-1,570328565		7,72891		-0,20318		0,840111		-17,2306		14,08993		-17,2306		14,08993

Таким образом, модель (5) зависимости цены квартиры Y от жилой площади квартиры Х₄ и от числа комнат в квартире Х₂ построена, ее уравнение имеет вид:

Построим множественную модель регрессии, учитывая все факторы (Х₄, Х₁, и Х₂):

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,876217908
R-квадрат	0,767757822
Нормированный R-квадрат	0,748404307
Стандартная ошибка	28,73687504
Наблюдения	40

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	3	98279,90622	32759,9687	39,6702	1,67E-11
Остаток	36	29729,08753	825,807987
Итого	39	128008,9938
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-5,643572321	12,07285417	-0,46745966	0,642988	-30,1285	18,84131	-30,1285	18,84131
X4	2,591405557	0,461440597	5,61590284	2,27E-06	1,655561	3,52725	1,655561	3,52725
X1	6,85963077	9,185748512	0,74676884	0,460053	-11,7699	25,48919	-11,7699	25,48919
X2	-1,985156991	7,795346067	-0,25465925	0,800435	-17,7949	13,82454	-17,7949	13,82454

Таким образом, трехфакторная модель (6) зависимости цены квартиры Y от жилой площади Х₄, города области Х₁ и числа комнат в квартире Х₂ построена, ее уравнение имеет вид:

Выберем лучшую из построенных моделей.

Для сравнения моделей с различным количеством учтенных в них факторов используем нормированные коэффициенты детерминации, которые содержатся в строке «нормированный R-квадрат» итогов инструмента «Регрессия». Чем больше величина нормированного коэффициента детерминации, тем лучше модель.

,

где - коэффициент детерминации, n – число наблюдений, k – число независимых переменных.

Модель (4): 0,767339455

Модель (5): 0,764160237

Модель (6): 0,767757821

Таким образом, лучшей является модель (6) зависимости цены квартиры Y от жилой площади Х₄, города области Х₁ и числа комнат в квартире Х₂:

Коэффициент регрессии β₁=6.859, следовательно, при изменении города области (Х₁), при одном и том же числе комнат в квартире (Х₂) и одной и той же жилой площади, цена квартиры (Y) увеличится в среднем на 6,859 тыс. долл.

Коэффициент регрессии β₂=-1.985, следовательно, при изменении числа комнат в квартире (Х₂) при одной и той же жилой площади (Х₄) и одном и том же городе области (Х₁), цена квартиры (Y) уменьшится в среднем на 1.985 тыс. долл.

Коэффициент регрессии β₃=2.591, следовательно, при увеличении жилой площади квартиры на 1 кв. м. (Х₄) при одном и том же городе области (Х₁) и одном и том же кол-ве комнат (Х₂), цена квартиры (Y) увеличится в среднем на 2.591 тыс. долл.

Свободный коэффициент не имеет экономического смысла, но говорит о том, что сначала меняется результат Y, а потом факторы X₁, X_2, X₄..