
- •Математический анализ. Часть 1.
- •Раздел 1. Введение в анализ: множества, функции.
- •Операции над высказываниями.
- •Предикаты. Кванторы общности и существования. Определение предиката.
- •Квантор общности.
- •Квантор существования.
- •П.2. Элементы теорий множеств (интуитивная теория множеств). Числовые множества. Множество действительных чисел.
- •Подмножества.
- •Операции над множествами.
- •Свойства операций над множествами.
- •1. Законы коммутативности.
- •2. Законы ассоциативности.
- •Универсальные множества. Дополнение и его свойства.
- •Бинарные отношения.
- •Запишем это бинарное отношение как множество пар:
- •Сужение функции.
- •Виды функций.
- •Композиция функций (сложная функция, суперпозиция функций.
- •Тождественная (единичная) функция.
- •Обратные функции.
- •1. , Где- единичная функция на.
- •Обратные тригонометрические функции.
- •2. Функция .
- •3. Функция arctg.
Сужение функции.
Определение. Пусть![]() ,
,![]() .
Сужением функции
.
Сужением функции![]() на множество
на множество![]() называется
называется![]() .
.
Пример. ![]() ;
;![]() ;
;![]() - область определения функции, отмечается
точками оси абсцисс.
- область определения функции, отмечается
точками оси абсцисс.![]() -
множество значений функции, отмечается
точками оси ординат.
-
множество значений функции, отмечается
точками оси ординат.
0

Рассмотрим сужения этой функции.
а)
![]() ;
;![]() для
для![]() .
.

б) ![]() ;
;![]() для
для![]()

Виды функций.
Определение. Функция![]() называется инъекцией (инъективным
отображением), если она обладает
свойством:
называется инъекцией (инъективным
отображением), если она обладает
свойством:
![]()
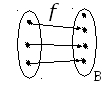
А
Рис. 1.
Используя закон контрапозиции можно дать другое определение инъекции, равносильное приведённому выше.
Функция
![]() называется инъекцией (инъективным
отображением), если она обладает
свойством:
называется инъекцией (инъективным
отображением), если она обладает
свойством:![]()
Определение. Функция![]() называется сюръекцией, если
называется сюръекцией, если![]() .
Сюръекция – это отображение «НА».
.
Сюръекция – это отображение «НА».

Рис.2.
В чём разница рисунков?
На рисунке 1 к некоторым точкам проведены
стрелки. Если к точке проведена стрелка,
то только одна. На рисунке 2 к каждой
точке множества
![]() проведена стрелка. К некоторым точкам
множества
проведена стрелка. К некоторым точкам
множества![]() может быть проведено несколько стрелок.
может быть проведено несколько стрелок.
О пределение.Функция
пределение.Функция![]() называется биекцией (взаимнооднозначным
отображением), если
называется биекцией (взаимнооднозначным
отображением), если![]() одновременно инъективно и сюръективно.
одновременно инъективно и сюръективно.
Задача (УИРС).
Пусть
![]() -
конечные множества.
-
конечные множества.![]() -
биекция.
-
биекция.
Что можно сказать про мощность множеств?
Пример. Определить вид следующих функций.
1 .
.![]() ;
;![]()
- не является инъекцией,
- сюръекция,
- не является биекцией.
2 .
.![]() ;
;![]()
- не является инъекцией,
- не является сюръекцией,
- не является биекцией.
3.
![]() ;
;![]()

- инъекция,
- сюръекция,
- биекция.
4 .
.![]() ;
;![]()
- инъекция,
- сюръекция,
- биекция,
Задача. (УИРС)
Пусть
![]() -
конечные множества.
-
конечные множества.![]() ,
,![]() .
.
Сколько существует инъекций
![]() таких, что
таких, что![]() ?
?
Сколько существует сюръекций
![]() таких, что
таких, что![]() ?
?
Сколько существует биекций
![]() таких, что
таких, что![]() ?
Какое условие существования этих
функций?
?
Какое условие существования этих
функций?
Композиция функций (сложная функция, суперпозиция функций.
Определение. Пусть![]() ,
,![]() .
Композицией функций
.
Композицией функций![]() и
и![]() (обозначается
(обозначается![]() )
называется такая функция, что её значение
)
называется такая функция, что её значение![]() определяется как
определяется как![]() для
для![]() .
.

![]()
Областью определения композиции является множество А.
![]()
Множеством значений композиции является множество С.
![]() ,
,
![]() -
внешняя функция,
-
внешняя функция,![]() -
внутренняя функция.
-
внутренняя функция.
Сначала на элементы действует внутренняя, а затем внешняя функция.
Пример.
![]() .
.
![]() .
.
![]() -
внешняя функция;
-
внешняя функция;![]() ,
,![]() ,
,![]() -
первая, вторая и третья внутренние
функции.
-
первая, вторая и третья внутренние
функции.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В общем случае композиция функций не коммутативна.
Теорема. Композиция функции
ассоциативна, т.е.![]()
![]() ;
;![]() ;
;![]() выполняется свойство:
выполняется свойство:![]()
![]()
Доказательство. Равенство![]() -
это равенство функций. Проверим выполнение
двух условия определения равенства
функций:
-
это равенство функций. Проверим выполнение
двух условия определения равенства
функций:
1)
![]()
2)
![]()
![]()
![]() .
.
Из 1) и 2) следует справедливость свойства
![]() .
.
Тождественная (единичная) функция.
Определение. Функция![]() называется тождественной (единичной)
функцией на множестве
называется тождественной (единичной)
функцией на множестве![]() ,
если
,
если![]()
![]() .
.
Свойства:
1. Пусть
![]() ,
,![]() -
тождественная функция на
-
тождественная функция на![]() ,
тогда
,
тогда![]()
Доказательство. Проверим выполнение условий определения равенства функций.
а)
![]() ,
,
б)
![]()
![]() .
.
Из а) и б) следует
![]()
2. Пусть
![]() ,
,![]() -
тождественная функция на
-
тождественная функция на![]() ,
тогда
,
тогда![]()
Доказательство.
а)
![]() ,
,
б)
![]()
![]() .
.
Из а) и б) следует
![]() .
.
