Бинарные отношения.

Определение.Бинарное отношение – это любое множество упоря­доченных пар. Другими словами, бинарное отношение – это подмножество прямого произведения двух множеств.

Пример.- бинарное отношение, которое называется отношением равен­ства на множестве натуральных чисел.

Бинарные отношения часто задают описанием.

Пример.Что такое отношение равенства на множестве?

Отношение равенства равно

Определение. Если отношение- подмножество прямого произведе­ния, то- бинарное отношение на множестве.

Изображение бинарных отношений графами.

Определение. Граф – это фигура на плоскости, состоящая из конеч­ного числа точек – вершин графа и линий – рёбер графа, соединяющих не­которые из вершин. Ребро графа – это линия, соединяющая какие-либо две вершины графа.

Пример. 1) Бинарное отношение задано как множество пар:

Изобразим бинарное отношение графом:

b

d

e

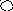
a

c

2) Бинарное отношение задано своим графом.

c

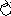
m

k

Запишем это бинарное отношение как множество пар:

llllllll

Определение. Разбиением множестваназывается такое семейство его непустых подмножеств, что каждый элемент множествавходит в точ­ности в один из членов семейства.

Другими словами, разбиением мно­жества называется совокупность его подмножеств, которые об­ладают следующими свойствами:

1. 

2. 

3. ,

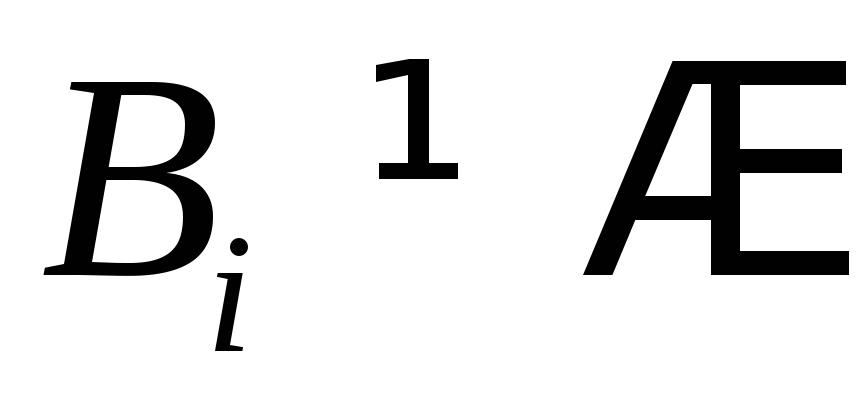
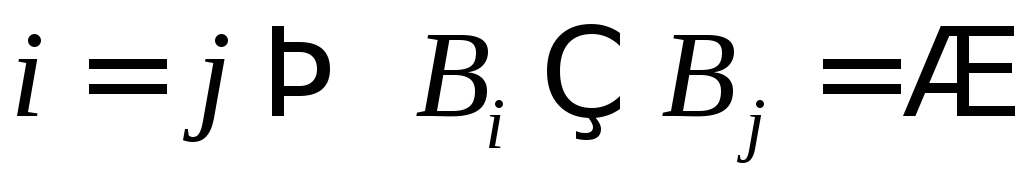
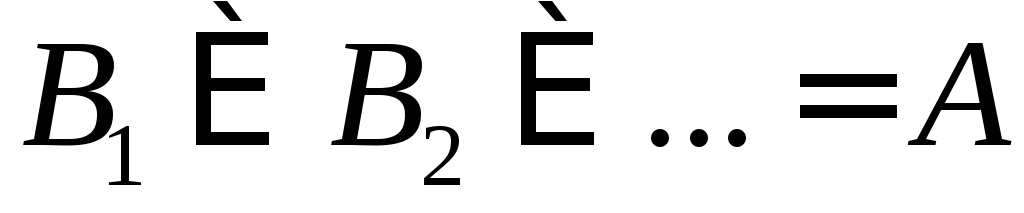т.е. разбиение множества есть свойство его не­пустых подмножеств, объединение которых совпадает с множеством, пересечение любых двух из них не пусто.

Пример. Пусть дано множество. Будут ли следующие се­мейства множеств разбиением.

1) ;;- являются разбиением

2) ;- являются разбиением

3) ;- не являются разбиением

Задача. (НИРС)

Пусть имеетэлементов. Сколько существует разбиений множе­ства.

п.2. Функции (отображения).

Пусть ,- множества.

Описание. Говорят, что задана функция, определенная на множествесо значениями в множестве, если в силу некоторого законакаж­дому элементуиз множествапоставили в соответствие единственный элемент в множестве.

или

- область определения;- область прибытия.

Слова «функция» и «отображение» - синонимы.

Если в силу некоторого закона элементупоставить в соответствие, то пишут:илиили.

Определение. Множество всех значений функции, которые она принимает на элементах множества, называется множеством значений функции.

Множество значений функции обозначается также иначе: .

Область значений функции обозначается: .

Определение. Графиком функции, определенной на множествеи принимающей значения во множественазывается множество.

Определение.Две функциииравны, если:

1. они имеют одинаковую область определения, т.е. ;

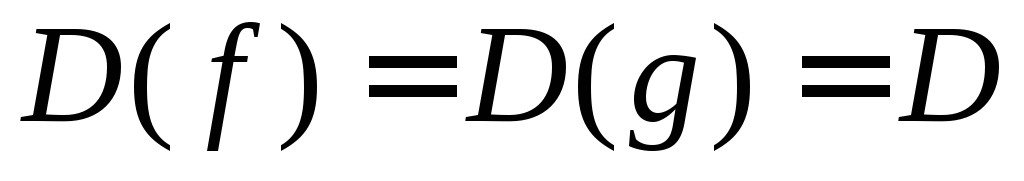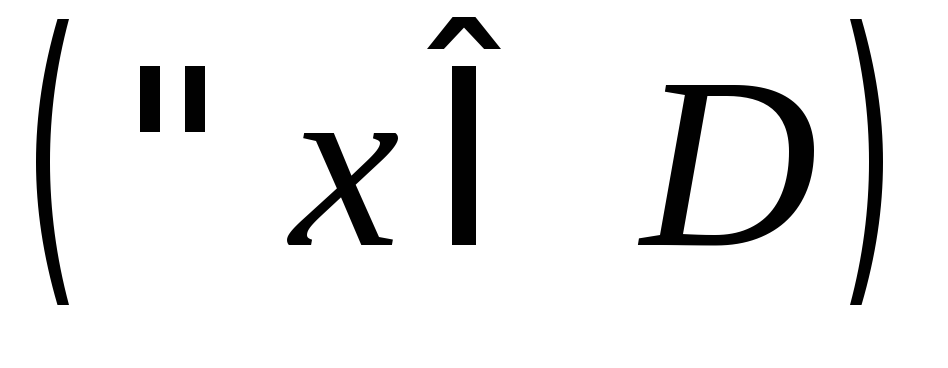2. значения этих функций равны:.

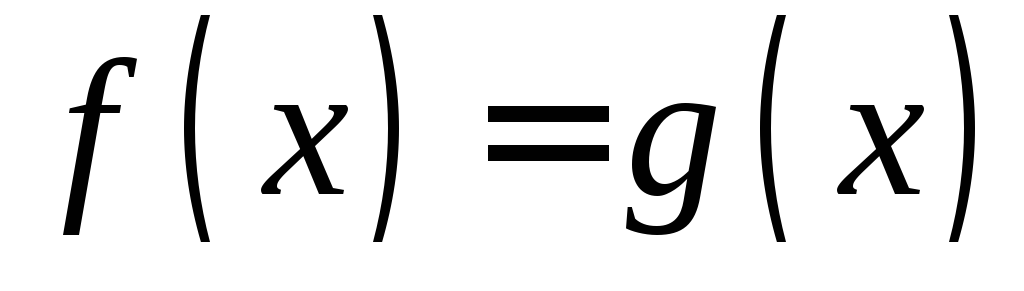Пример. Пусть;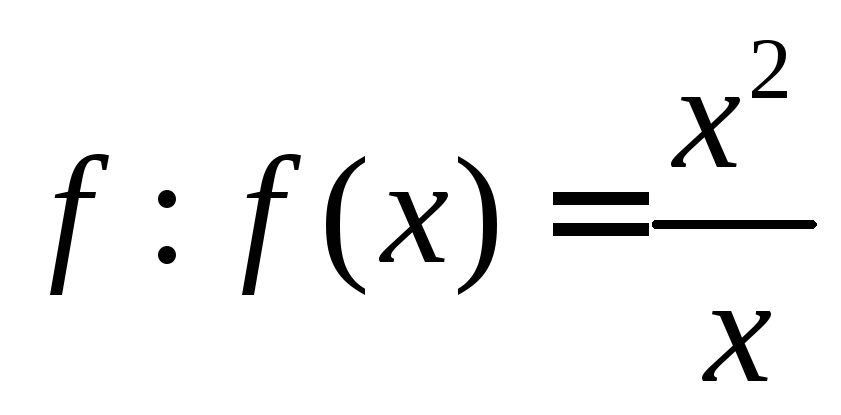

. Будут ли эти функции равны?

Решение. Проверим выполнение условий определения равенства функций.

,.

Числовая функция. Пусть задана функция. Если элементами множествиявляются действительные числа, т.е.то функциюназывают числовой функцией и часто записывают в виде

Числовая функция есть функция, у которой как область определения, так и множество значений, где– множество действительных чисел.

Для задания числовой функции может быть использован аналитический способ (в виде формулы ), табличный и графический. (Эти способы известны из курса средней школы).

Основные характеристики функции.

1) Ограниченность на множестве.

Функция ,определённая на множестве, называется ограниченной на этом множестве, если существует такое число,что для всехвыполняется неравенство.

Или

называется ограниченной на

2) Чётность и нечётность.

Функция ,определённая на множестве, называется чётной

.

Функция ,определённая на множестве, называется нечётной

.

3) Монотонность функции. Возрастающие и убывающие функции на множественазываются строго монотонными на этом множестве. Монотонными функциями на множественазываются возрастающие, невозрастающие, убывающие и неубывающие функции на этом множестве.

Функция ,определённая на множественазывается возрастающей на множестве, если.

Функция ,определённая на множественазывается неубывающей на множестве, если.

Функция ,определённая на множественазывается убывающей на множестве, если.

Функция ,определённая на множественазывается невозрастающей на множестве, если.

4) Периодичность функции. Функция,определённая на множественазывается периодической на этом множестве, если. Числоназывается периодом функции. Если- период функции, то её периодами будут также числа