20

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Всероссийский заочный финансово-экономический

ИНСТИТУТ

Филиал в г. Брянске

Кафедра экономико-метематических моделей

_{ЭКОНОМЕТРИКА}

_{Конспект лекции 3}

_{(часть 2)}

В.М. Малашенко

Применение обобщенного метода наименьших квадратов для оценивания параметров эконометрических моделей

ПЛАН

1.1. Предпосылки обычного метода наименьших квадратов 2

1.2. Свойства оценок обычного метода наименьших квадратов 5

2. ОБОБЩЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 6

2.1. Обобщенная модель регрессии 6

2.2. Оценивание параметров моделей с гетероскедастичностью возмущений 10

Пример 1 13

2.3. Оценивание параметров моделей с коррелированными возмущениями 16

Пример 2 17

ЛИТЕРАТУРА 20

ОБЫЧНЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

1. Предпосылки обычного метода наименьших квадратов

Пусть рассматривается возможность построения линейной модели множественной регрессии. В матричной форме модель имеет вид:

,

(0)

где Y— вектор значений результатаYразмераn;X— матрица значений факторов размера;— вектор параметров модели размера;— вектор возмущений размераn.

Уравнение регрессии модели (0) в матричной форме выглядит следующим образом:

,

(0)

где — вектор предсказываемых уравнением регрессии значений результатаYразмераn; b— вектор оценок параметров модели по выборочным наблюдениям размера.

Указанные матрицы имеют вид:

; ;;;;.

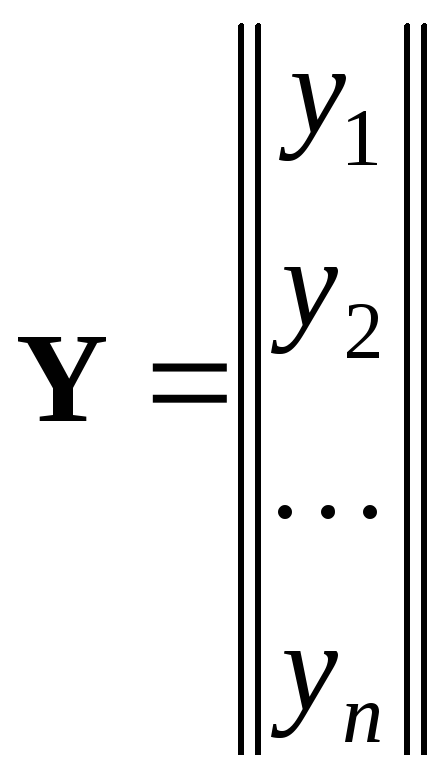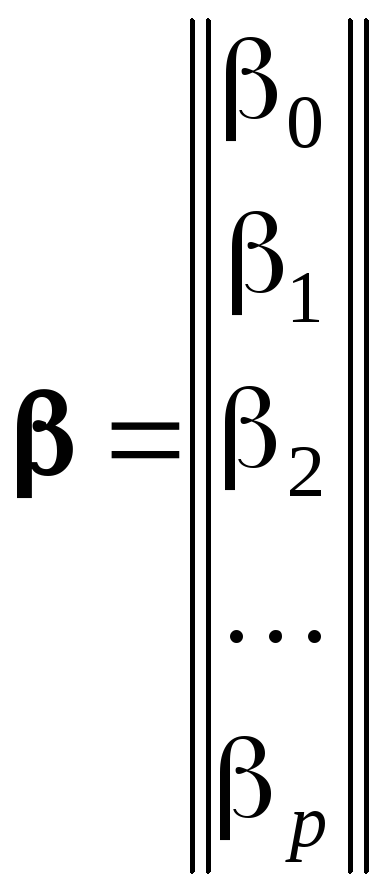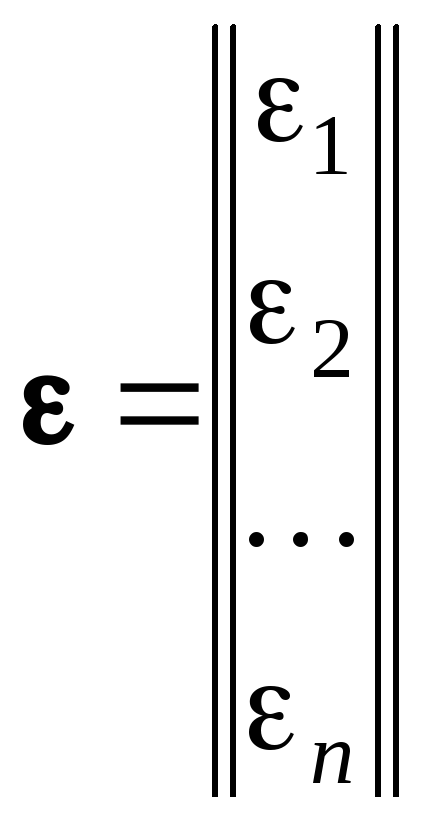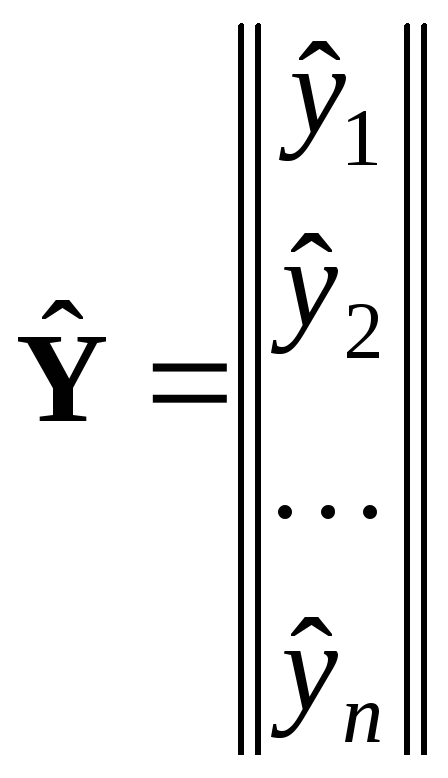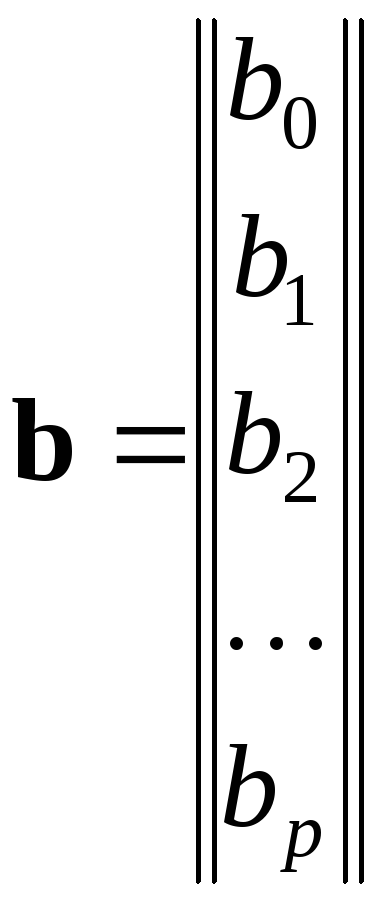Разность матриц Yиявляется вектором-столбцом остатков размераn:

.

(0)

Условие обычного метода наименьших квадратов(Ordinary Least Squares) в матричной форме записывается как

,

(0)

откуда вектор оценок bпараметров модели (0) определяется по формуле

.

(0)

(Индекс «^T» обозначает операцию транспонирования матриц, а индекс «–1» — операцию обращения матриц.)

Для получения несмещенных, эффективных и состоятельных оценок параметров модели (0) необходимо выполнение следующих предпосылок:

1.Возмущение_i(i=1, 2, …, n) есть величина случайная, а факторыX₁,X₂, …,X_p— величины неслучайные. Это означает, что вектор возмущений— случайный вектор, а матрица значений факторовX— неслучайная (детерминированная).

Проверка выполнения этой предпосылки может проводиться с помощью разных критериев. Наиболее простыми из них являются метод серийиметодповоротных точек, которыми исследуется ряд остатков регрессии. Иногда достаточным оказывается визуальный анализ графика (графиков) остатков.

2.Математическое ожидание возмущения равно нулю_i:

(i=1, 2, …, n).

(0)

Другими словами, математическое ожидание вектора возмущений есть нулевой вектор размераn:

.

(0)

Данная предпосылка всегда выполняется для линейных моделей и моделей, нелинейных по переменным. Для моделей,нелинейных по параметрами приводимых к линейному виду логарифмированием, предпосылка выполняется для логарифмов исходных данных.

3.Дисперсия возмущения одинакова для всех наблюдений результатаY:

(i=1, 2, …, n).

(0)

Это условие называется условием гомоскедастичностиилиравноизменчивостивозмущений. В матричной форме данная предпосылка имеет вид:

,

(0)

где I_n— единичная матрицаn-го порядка.

Выполнение этой предпосылки может проверяться разными методами. Ниже рассмотрена процедура проверки предпосылки методом Голдфельда–Квандта.

4. Возмущения не коррелированны между собой. Это означает, что ковариация между отдельными возмущениями_jи_k() равна нулю:

(0)

где (_j) и(_k) равны нулю в силу предпосылки2.

Матричная форма записи предпосылки 4имеет вид:

,

(0)

где — ковариационная матрица возмущений

,

(0)

в которой все элементы, не лежащие на главной диагонали, равны нулю, а все элементы, лежащие на главной диагонали, равны одной и той же дисперсии :

(i=1, 2, …, n).

(0)

Равенство (0)вытекает из определения дисперсии и предпосылки2. Так в соответствии с определением,дисперсией²(Z) некоторой случайной величиныZназывается математическое ожидание квадрата ее отклонения от математического ожидания:. Согласно предпосылке2, отсюда

.

(0)

Видно, что матричные записи условий предпосылок 3и4— (0) и (0) соответственно, совпадают. Проверка выполнения предпосылки4с помощьюd‑статистики Дарбина–Уотсона рассмотрена ниже.

5.Возмущение_iесть нормально распределенная случайная величина, а вектор возмущений— нормально распределенный случайный вектор:

.

(0)

Обоснованием такого допущения служит центральная предельная теорема теории вероятностей, согласно которой сумма большого числа случайных величин имеет приближенно нормальное распределение независимо от индивидуального распределения слагаемых. Отклонение фактических значений результата Yот теоретических вызывается, как правило, множеством случайных и неучтенных факторов, каждый из которых не оказывает доминирующего влияния. Поэтому нормальное распределение является приемлемой моделью суммарной погрешности, т. е. возмущения.

Выполнение этой предпосылки может проверяться разными способами, например, с помощью R/S-критерия.

6.Матрицаявляетсянеособенной, т. е. ее определитель не равен нулю. Это означает, что столбцы матрицы значений факторовXдолжны быть линейно независимыми. Следовательно матрицаXдолжна иметь максимальный ранг: , гдеp— число факторов в модели. Кроме того, число наблюденийnдолжно превосходить ранг матрицыX:

,

(0)

поскольку в противном случае невозможно получение сколько-нибудь надежных статистических выводов.
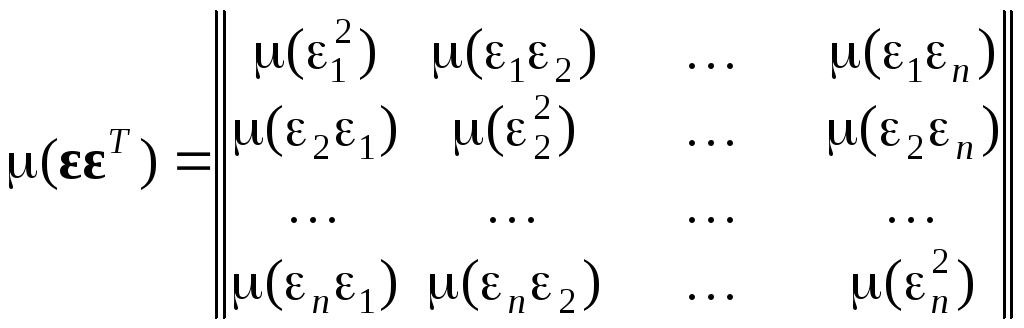