
adambaev_avtomatty
.pdf
Автоматты басқару теориясы
[12]. Сондыºтан, экспериментальды |
берiлiстердi ж¼ндеу |
¸дiстерiн толы¹ыраº ºарастырамыз. |
|
2.1.1. Е» кiшi квадраттар ¸дiсi (КК°) бойынша, сызыºты объектiлердi» функционалдыº т¸уелдiлiгiн аныºтау
Те»деудi экспериментальды аныºтау кезінäå, ¼лшемдiлiк ºате болады. ´лшеу процесi кезiнде ол ºатенi жою¹а тырысады, сонымен ºатар ºатенi берiлiстердi ж¼ндеу кезінäå де азайту¹а тырысады. Б½л жолдарды» бiрi – КК° болып табылады. Егер ºателiктер ºалыпты ¾лестiрiмге статистикалы т¸уелсiз болса (корреляциялы емес), ¸дiс – ыºтималдыº ºорытынды бередi. °дiстi ºолдану жа¹дайы, экспериментальды ¼лшемдiлiктер сандарыны» к¼птiгiне байланысты. Егер бiр белгiсiз ¼лшенетiн болса, онда бiр эксперимент болу керек. Бiраº, бiрнеше эксперимент ж¾ргiзiліп, ºорытындылар орталанады. Б½л жа¹дайда орталау КК°-мен орындалады.
Айталыº, белгiсiз õ ìүøåñií àíûºòàó ¾øií n ¼ëøåì ¼òêiçiëåäi. ´ëøåмäåðäi» áåðiëiñòåði: y1,y2,...,yn. y1-x, y2-x,…, yn-x айырымы мен оларды» квадратын (y1–x)2, (y2–x)2,..., (yn–x)2 º½растырамыз. õ ìүшесiн, квадраттарды» ºосындысы минимальды болатындай та»дап, мынаны аламыз:
n |
|
å(yi - x)2 ® min |
(2.1) |
i=1
Осы¹ан келесi шарт тура келедi:
немесе
Á½äàí àëàтынымыз:
|
|
n |
|
|
|
|
¶å(yi - x)2 |
= 0 |
|
||
|
i =1 |
|
|||
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 × å(yi - x)2 = 0 . |
|
|||
|
|
|
i =1 |
|
|
|
|
1 |
n |
|
|
x = |
× å yi . |
|
(2.2) |
||
n |
|
||||
|
|
i =1 |
|
|
|
Егер кейбiр ¼лшемдiктер наºты те» болмаса, онда келесi шаманы минимумдау керек:
n |
1 |
× (y |
- x)2 ¾¾®min |
(2.3) |
|
|
|||||
åi=1 si2 |
|||||
i |
X |
|
|||
49
М.Д. Адамбаев, Т.С. Малдыбаева
ì½íäàғы si2 - жеке ¼лшемдiлiк ºателiгi, дисперсиясы. si2 = const бол¹анда (2.1) ¼рнектi аламыз.
Бiрнеше топтар арасында¹ы функционалдыº т¸уелдiктi ¼лшеу кезiнде, б½л ¸дiс ¼те ºиын жолмен есептеледі. Îë үшін мысалдар ºарастырыл¹ан.
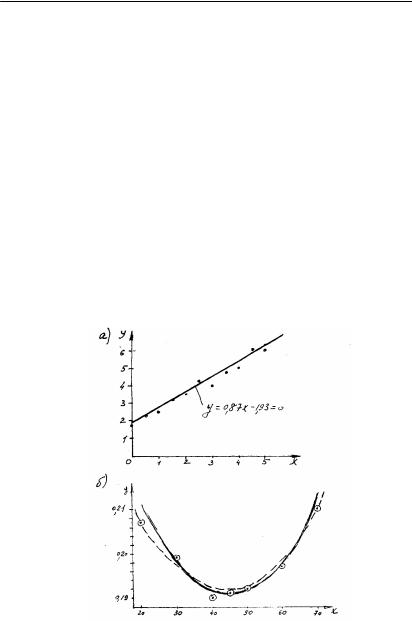
2.1-мûñàë. 2.1-кесте мен 2.1à-суретте сызыºты динамикалыº ж¾йенi» статикалыº сипаттамасын экспериментальды аныºтау берiлiстерi келтiрiлген.
2.1-кесте
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
n=1 |
|
xi |
0,0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
å xi |
= 27,50 |
yi |
1,75 |
2,3 |
2,5 |
3,2 |
3,5 |
4,25 |
4,0 |
4,7 |
5,0 |
6,0 |
6,0 |
å yi |
= 43,20 |
xi2 |
0,0 |
0,25 |
1,0 |
2,25 |
4,0 |
6,25 |
9,0 |
12,25 |
16,0 |
20,25 |
25 |
å xi2 |
= 96,25 |
xi ƒyi |
0,0 |
1,15 |
2,5 |
4,8 |
7,0 |
10,62 |
12,0 |
16,45 |
20,0 |
27,0 |
30,0 |
å xi ƒyi = |
|
|
|
|
|
|
|
|
|
|
|
|
|
131,45 |
|
2.1-сурет. а) ñûçûºòûº; ə) ñûçûºòûº åìåñ ò¸óåëäiëiêòi òåãiñòåó
50

Автоматты басқару теориясы
Ендi КК° бойынша объектiнi» õ êiðiñi мен ó шы¹ысы арасында¹ы статикалыº т¸уелдiлiктi» шамасын табу керек.
Øåøiìi. Бастапºы т¸уелдiлiктi мына түрде жазамыз:
y + Ax + B = 0 . |
(2.4) |
õi æ¸íå yi -òi» åêi ì¸íäåðií àëсақ жеткiлiктi, табыл¹ан екi те»деуден À æ¸íå Â-ны табу керек. Біраº о¹ан басºа экспериментальды õi æ¸íå yi шамаларын ºойғанмен, те»деудi ºана¹аттандырмайды:
yi + Axi + B = di ¹ 0 . |
(2.5) |
|
Àëøàºòûºòàð di , геометриялыº к¼зºараста (õi, yi) |
||
н¾ктелерiнен алын¹ан ó + Àõ + Â = 0 |
òå»äåóiìiçãå |
äåéiíãi |
аралыººа те». Б½л т¾зудi, я¹ни оны» À |
æ¸íå  параметрлерi, |
|
алшаºтыºты» орта м¸нi минимальді болатындай та»дап аламыз. Гауссты» КК° алшаºтыºтар квадратыны» ºосындысы минимальді ådi2 = min болатындай т¾зу ж¾ргiзедi.
°дiстi ºолдан¹ан жа¹дайда di кездейсоº шама деп, ал
за»ы ¾лестiрiм нормальды деп аламыз. Айталыº, бiрдей шартта õi æ¸íå yi шамаларын ¼лшегенде (2.4) ¾шiн алын¹ан
келесi алшаºтыºтар d1,d2 ,d3 ,....,dn |
болсын. |
|
|
|
|
|||||||||||||||||||
|
|
|
Бiр-бiрiмен байланысы жоº т¸уелсiз алшаºтыºтарды» |
|||||||||||||||||||||
|
|
бiрлестiк ыºтималдыºта пайда болуы, ыºтималдыºтар |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ê¼áåéòiíäiñiíå òå»: |
|
|
|
|
|
|
||||||||
1 |
|
|
-d12 |
|
1 |
|
|
-d 22 |
|
1 |
|
|
-d n2 |
|
æ 1 |
|
ö |
n |
- |
1 |
×(d12 +d 22 +×××+d n2 ) |
(2.6) |
||
|
|
2s 2 |
|
|
|
2s 2 |
|
|
|
2s 2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
×е |
|
× |
|
|
× е |
|
×××× |
|
|
×е |
|
= ç |
|
|
÷ |
|
×e |
2s |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
s × 2p |
|
|
s × 2p |
|
|
|
s × 2p |
|
|
|
ès × 2p ø |
|
|
|
|
|
|||||||
À æ¸íå  константаларды» м¸ндерi ыºтималды, ал егер б½л шама е» ¾лкен болса, ол келесi жа¹дайда орындалады:
n |
|
d12 + d 22 + ××× + d n2 = ådi2 = min . |
(2.7) |
i=1
n
åd i2 минимумi квадраттыº орта алшаºтыºты» минимумiн
i =1
бередi:
n
ådi2
s = i =1 n
51

М.Д. Адамбаев, Т.С. Малдыбаева
n
ådi2 минимуміí àëó ¾øií À мен  ºàëàé òà»äàï àëó
i=1
керек? Эстремум бар болуды» ºажеттi шартын аныºтайтын те»деулер, е» негiзi болып саналаäû:
|
|
n |
|
|
|
|
|
n |
|
|
|
¶ådi2 |
|
|
|
¶ådi2 |
= 0 . |
|
|||
|
i |
=1 |
|
= 0 |
æ¸íå |
|
|
i=1 |
(2.8) |
|
|
|
¶A |
|
|
|
¶B |
||||
|
|
|
|
|
|
|
|
|
||
Оларды алу ¾шiн, эксперименттен алын¹ан м¸ндерден |
||||||||||
те»деулердi» шартты ж¾йесiн º½рады: |
|
|
||||||||
|
|
|
y1 + Ax1 + B = d1 ; ü |
|
|
|||||
|
|
|
y2 + Ax2 |
+ B = d |
|
ï |
|
(2.9) |
||
|
|
|
2 |
;ï |
|
|||||
|
|
|
...................... |
|
|
ý |
|
|
||
|
|
|
|
ï |
|
|
||||
yn + Axn + B = d n .ïþ
°р шартты те»деудi, квадрат д¸режеге шы¹арады:
2 |
|
2 |
2 |
|
2 |
|
|
2 |
ü |
|
y1 |
+ A |
|
x1 |
+ B |
|
+ 2 Ax1 y1 + 2By1 |
+ 2 ABx1 = d1 , |
ï |
|
|
y12 |
+ A2 x22 |
+ B 2 |
+ 2 Ax2 y2 + 2By2 |
+ 2 ABx2 |
= d 22 |
,ï |
(2.10) |
|||
........................................... |
|
|
ý |
|
||||||
|
|
ï |
|
|||||||
2 |
+ A |
2 |
2 |
+ B |
2 |
+ 2 Axn yn + 2Byn |
+ 2 ABxn |
2 |
ï |
|
yn |
|
xn |
|
= d n |
.þ |
|
||||
Б½ларды» б¸рiн ºосамыз:
å yi2 + A2 åxi2 + +nB 2 + 2Aåxi yi + 2Bå yi +
Б½дан екi нормаль те»деуін табады:
¶ådi2 = 2 Aåxi2 + 2åxi yi + ¶A
¶ådi2 = 2nB + 2å yi + 2 Aå ¶B
немесе
2 ABåxi = ådi2 . (2.11)
2B |
å |
x |
|
ü |
|
i |
= 0;ï |
(2.12) |
|||
|
|
ï |
|||
|
|
|
|
ý |
|
xi = 0 |
|
|
ï |
|
|
|
|
ï |
|
||
|
|
|
|
þ |
|
Aåxi2 + Båxi = -åxi yi , Aåxi2 + B × n = -å yi ,
52

Автоматты басқару теориясы
б½л жерден À мен Â ыºтималдыº м¸ндерiн есептейдi.
²арастырылып |
îòûð¹àí |
сандыº |
мысал |
¾øií: |
n =11; åxi = 27,5; åyi |
= 43,20; åxi2 |
= 96,25; åxi yi |
=131,45 |
сандары |
2.1-кестеде есептелiнген. Берiлген мысал үшiн нормаль те»деулер мына ò¾ðде болады:
96,25ƒA + 27,5ƒÂ = -131,45.
27,5ƒA + 11ƒB = -43,20.
Б½äàí:
A= -131,45 ×11- 43,2 × 27,5 = -0,87; 96,25 ×11 - 27,5 × 27,5
B= 96,25 × 43,2 - 27,5 ×131,45 = -1,93. 96,25 ×11 - 27,5 × 27,5
Iзделген орталан¹ан те»деу мына ò¾ðãå êåëäi:
y - 0,87ƒx - 1,93 = 0.
2.1à-суретiнде с¸йкес келетiн сызыº к¼рсетiлген .
õ æ¸íå ó арасында¹ы т¸уелдiлiктi y + Ax + B = 0 т¾рiнде зерттегенде, øû¹ûñ – ó шамасы мен кiрiс – õ øàìàсыны» экспериментальды ¼лшенуi д¸лiрек болады. Б½л практикада жиi кездеседi. Егер керi жа¹дай болса, онда т¸уелдiлiктi мына т¾рде iздейдi:
y + A1 x + B1 = 0. |
(2.13) |
À1 мен Â1 константаларды мына те»деулер табады:
|
|
|
|
2 |
|
|
|
|
|
ü |
|
|
A1 |
× å yi |
+ B1 × å yi |
= -åxi |
× yi |
(2.14) |
|||||||
;ï |
||||||||||||
A |
× |
å |
y |
|
+ B × n = - |
å |
x |
. |
|
ý |
|
|
i |
|
ï |
|
|||||||||
1 |
|
|
1 |
i |
|
|
þ |
|
||||
(2.4) ж¸не (2.13) т¾рiндегi те»деулерге е» кiшi квадраттар ¸дiсiн (ЕКК°) ºолдану бiрдей ºорытынды бермейдi (2.1,ə- суретте графиктегi сызыºтар т½таспайды). Б½л туралы толы¹ыраº [7] ¸дебиетте берiлген.
53

М.Д. Адамбаев, Т.С. Малдыбаева
2.1.2. Сызыºтыº емес объектiлердi» функционалдыº т¸уелдiлiêòåðií àíûºòàó
2.2-мûñàë. 2.2-кесте мен 2.1ə-суретiнде сызыºтыº емес объектiнi» статистикалыº сипаттамасын аныºтайтын эксперименттi» ºорытындысы келтiрiлген (ксантагенат т½тынуыны» ºалдыºта¹ы мыс м¼лшерiне ¸серi, %).
2.2-кесте
i – í¾êòåíi» í¼ìiði |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
õ –êiðiñ |
20 |
30 |
40 |
45 |
50 |
60 |
70 |
|
|
|
|
|
|
|
|
y – øû¹ûñ |
0,207 |
0,199 |
0,19 |
0,191 |
0,192 |
0,197 |
0,21 |
|
|
|
|
|
|
|
|
Е» кiшi квадраттар ¸дiсi бойынша объектiнi» кiрiсi – õ æ¸íå øû¹ûñû – y арасында¹ы аналитикалыº т¸уелдiлiктi аныºтау керек.
Øåøiìi. Алдымен аналитикалыº т¸уелдiлiктi» т¾рiн аныºтау керек. Экспериментальдыº берулiлер бойынша (2.1ə- сурет) алын¹ан н¾телердi параболамен тегiстеуге болады:
y = A + Bx + Cx2 . |
(2.15) |
Мұндағы маºсат – А, В, С константаларды» ыºтималдыº м¸ндерiн аныºтау. Бiрiншi ºадамда А’, В’, С’ жуыº шамалар аныºталады. Б½л ¾шiн ¾ш кез келген экспериментальды н¾ктелердi алып, оларды» координаталарын бастапºы те»деуге ¾ш рет ºоямыз. Б½л бiзге ¾ш те»деудi бередi, одан жуыº А’, В’, С’ м¸ндерi аныºталады. Кiрiс ¼згерiсiнi» берiлген аралы¹ынан бiрºалыпты ¾лестiрiлген н¾телердi ал¹ан ж¼н. А’, В’, С’ тауып, е» кiшi квадраттар ¸дiсi бойынша коэффицеттердi» т¾зетулерiн табамыз.
А’,В’,С’ аныºтау ¾шiн 2.2-кестеден бастапºы параболаны» контурын д¸лдiрек бейiмдейтiн, 1, 4 æ¸íå 7 í¾òåëåрді аламыз. Одан мына те»деулердi аламыз:
0,207 = A' + B ' × 20 + C ' × 202 ü |
|
||||||||
0,131 = A' + B ' × 45 + C ' × 452 |
ï |
(2.16) |
|||||||
ý |
|||||||||
0,21 = A |
' |
+ B |
' |
×70 + C |
' |
×70 |
2 |
ï |
|
|
|
|
|
þ |
|
||||
54

Автоматты басқару теориясы
(2.16)-äàí A' = 0,245; B ' = -0,246 ×10-2 ; C ' = 0,28 ×10-4 |
есептеймiз. |
|||||
Ендi т¾зетулердi қарастырамыз: |
|
|
|
|
||
A = A' |
+ DA = 0,245 + DA |
|
ü |
|
||
B = B ' |
|
|
|
ï |
(2.17) |
|
+ DB = -0,246 ×10 -2 + DBý |
||||||
C = C |
' |
+ DC = 0,28 ×10 |
-4 |
+ DC |
ï |
|
|
|
þ |
|
|||
Åíäi y ' = A' + B' × x + C ' × x 2 жуыº параболадан эксперимен-
тальды н¾кте ординаталарыны» ауытºуын табамыз. Ол ¾шiн параболаны» те»деуiне õi экспериментальды берiлулерiне с¸йкес келетiн x1=20; x2=30; ….; x7=70 ì¸íäåðін ºоямыз:
y1' |
= A' + B' |
× x1 |
+ C ' × x12 |
= 0,245 - 0,246 ×10-2 |
× 20 + 0,28 ×10 -4 |
× 202 |
= 0,207; |
y2' |
= A' + B' |
× x2 + C ' × x22 |
= 0,245 - 0,246 ×10 -2 |
× 30 + 0,28 ×10-4 |
× 302 |
= 0,1964; |
|
y3' |
= 0,1914; y4' |
= 0,1912; y5' = 0,1920; y6' = 0,1980; y7' = 0,2100. |
|
||||
С¸йкес келетiн экспериментальды ói шамалардан, табыл¹ан сандарды алып тастап, мынаны аламыз:
Dy1 = 0,207 - 0,207 = 0,00;
Dy2 = 0,1990 - 0,1964 = 0,26 ×10 -2 ;
Dy3 = 0,1900 - 0,1214 = -0,14 ×10-2 ;
Dy4 = 0,1910 - 0,1912 = -0,02 ×10-2 ;
Dy5 = 0,1920 - 0,1920 = 0,00;
Dy6 = 0,1970 - 0,1980 = -0,1×10-2 ;
Dy7 = 0,2100 - 0,210 = 0,00.
DA, DB , DC |
т¾зетулердi |
төмендегідей |
àíûºòàлаäû. |
||
yi = (A' + DA)+ (B ' + DB)× xi + (C ' + DC )× xi2 |
òå»äåóiíå |
A' + DA, |
|||
B' + DB, C' + DC |
ºîéûï îäàí, |
yi1 = A' + B' × xi + C ' × xi2 |
òå»äåóií |
||
алып, т¾зетулердi есептеуге ºажет те»деудi аламыз: |
|
||||
yi - yi' = Dyi = DA + DB × xi + DC × xi2
55

М.Д. Адамбаев, Т.С. Малдыбаева
немесе сандыº т¾рде:
DA + DB × 20 + DC × 202
DA + DB × 30 + DC × 302
DA + DB × 40 + DC × 402
DA + DB × 45 + DC × 452
DA + DB × 50 + DC × 502
DA + DB × 60 + DC × 602
DA + DB × 70 + DC × 702
= 0,00 |
ü |
= 0,26 ×10-2 |
ï |
ï |
=-0,14 ×10-2 ï
ï(2.18)
=-0,02 ×10-2 ïý
= 0,00 |
ï |
|
ï |
||
|
||
= -0,1×10 |
-2 ï |
|
= 0,00 |
ï |
|
ï |
||
|
þ |
Б½л ж¾йеде, белгiсiз м¾шелердi» санына ºара¹анда,
те»деулердi» саны к¼п. Ендi D À, D  æ¸íå D Ñ ыºтимал м¸ндерiн есептеу ¾шiн ЕКК° ºолдану керек. Ол ¾шiн барлыº те»деулердi квадраттап ºîñып, содан кейiн:
|
¶åDyi2 |
= 0; |
¶åDyi2 |
|
= 0; |
¶åDyi2 |
= 0 |
(2.19) |
|
¶DB |
|||||||
|
|
|||||||
|
¶DA |
DC |
||||||
|
|
|
|
|
||||
шарттан D À, D  æ¸íå D Ñ |
есептеп |
øû¹àðó |
¾øií ¾ø |
|||||
нормаль те»деудi алу керек. Шартты ж¾йенi нормаль т¾рге тез т¾рлендiрудi келесi ереже бойынша ж¾ргiзуге болады:
-бiрiншi нормаль те»деудi º½ру ¾шiн, осы те»деудегi бiрiншi т½р¹ан белгiсiздi» коэффициентiне ¸рбiр шартты те»деудi к¼бейтіп, алын¹ан те»деулердi ºосу керек;
-екiншi нормаль те»деудi º½ру ¾шiн, осы те»деудегi
екiншi т½р¹ан белгiсiздi» коэффициентiне ¸рбiр шартты те»деудi к¼бейтіп, барлыº алын¹ан те»деудi ºосу керек. Сол сияºты ары ºарай ж¾ре бередi. ²анша белгiсiздiк болса, сонша нормаль те»деу алынады. Б½л ереженi 2.1-мысал ¾шiн
де ºолдану¹а болады. (2.18) барлыº те»деуiнде бiрiншi D À белгiсiздiктi» коэффициентi 1-ге те» бол¹андыºтан, бiрiншi нормаль те»деудi алу ¾шiн, те»деулердi ºоссаº жеткiлiктi:
D Aƒ7+ D Bƒ315+ D Cƒ15925=0,00.
Екiншi нормаль те»деудi алу ¾шiн, мыналарды ºосу ºажет:
56

Автоматты басқару теориясы
DА × 20 + DВ × 20 × 20 + DС × 202 × 20 = 0,00 × 20;
DA ×30 + DB ×30 ×30 + DC ×302 ×30 = 0,26 ×10 2 ×30;
DA × 40 + DB × 40 × 40 + DC × 402 × 40 = -0,14 ×10-2 × 40;
DA × 45 + DB × 45 × 45 + DC × 452 × 45 = -0,02 ×10-2 × 45;
DA ×50 + DB ×50 ×50 + DC ×502 ×50 = 0,00 ×50;
DA × 60 + DB × 60 × 60 + DC ×60 2 × 60 = -0,1×10 -2 × 60;
DA × 70 + DB × 70 × 70 + DC ×70 2 × 70 = 0,00 ×70.
Б½дан алатынымыз:
D Aƒ315+ D Bƒ15925+ D Cƒ874125=-4,7ƒ10-2.
¶шiн нормаль те»деудi алу ¾шiн та¹ы да мыналарды ºосу ºажет:
DА × 202 |
+ DВ × 20 × 202 |
+ DС × 202 × 202 |
= 0,00 × 202 ; |
||
DA ×302 |
+ DB ×30 ×302 |
+ DC ×302 ×302 |
= 0,26 ×102 ×302 ; |
||
DA × 402 |
+ DB × 40 × 402 |
+ DC × 402 × 402 |
= -0,14 |
×10-2 × 402 ; |
|
DA × 452 |
+ DB × 45 × 452 |
+ DC × 452 |
× 452 |
= -0,02 |
×10-2 × 452 ; |
DA ×502 |
+ DB ×50 ×502 |
+ DC ×502 ×502 |
= 0,00 ×502 ; |
||
DA ×602 |
+ DB × 60 ×602 |
+ DC × 602 |
× 602 |
= -0,1×10-2 ×602 ; |
|
DA ×702 |
+ DB × 70 ×702 |
+ DC × 702 |
× 702 |
= 0,00 × 702. |
|
Б½дан аламыз:
D Aƒ15925+ D Bƒ874125+ D Cƒ50850625=-3,905. Табыл¹ан ¾ш нормаль те»деуден:
D Aƒ7+ D Bƒ315+ D Cƒ15925=0,00;
D Aƒ315+ D Bƒ15925+ D Cƒ874125=-4,7ƒ10-2; D Aƒ15925+ D Bƒ874125+ D Cƒ50850625=-3,905;
57

М.Д. Адамбаев, Т.С. Малдыбаева
т¾зетулер есептелiнедi:
DÀ = 0,0581 = 0,0083; 7
DB = 1,7216125 = -0,0221×10-2 ; 7809,375
DC = 0,0056875 = 0,0073×10-4. 7809,375
Алдында жуыº есептеген параболаны» параметрлерiне (2.17) т¾зетулердi енгiзе отырып, мынаны аламыз:
А = А' + DA = 0,245 + 0,0083 = 0,2533;
B= B' + DB = -0,246 ×10-2 - 0,0221×10-2 = -0,2681×10-2 ;
C= C ' + DC = 0,28 ×10-4 + 0,0073×10-4 = 0,2873×10-4.
Б½л кезде орталан¹ан параболаны» те»деуi мына т¾рге келтiрiледi:
y = 0,2583 - 0,2681ƒ102 ƒx + 0,2873ƒ10-4 ƒx2 (2.20)
2.1ə-суретiнде экспериментальды н¾ктелер, жуыº (штрих сызыº) ж¸не орталан¹ан параболалар келтiрiлген. Д¸лденген коэффициенттер – объектiлердi басºару ж¾йесі ж½мысыны» техника-экономикалыº есебiнде ºолданылады.
2.2. Екпiн ºисы¹ы бойынша объект те»деулерiн аныºтау
Объект те»деулерiн алу ¾шiн, бiр немесе бiрнеше ауыспалы процестердi ¼лшеу əрі реттеу мақсатында эксперимент ¼ткiзедi. Б½л процестер iзделген дифференциалды те»деудi» дербес шешiмiне с¸йкес келедi.
Автоматтандыруда эксперименттi» екi т¾рi ке» ºолданылады: екпiн ºисы¹ы жəне жиiлiктiк сипаттамаларды алу. Бiрiншi жа¹дайда – içäåëiï
58
