Матем1

Aa- Ә(ә)

және нүктелерінің арақашықтығы тең...

Ж: 5

және нүктелерінің арақашықтығы тең...

Ж: 5

Айқындалмаған түрде берілген функциясының (4;0) нүктесіндегі туындысын тап

Ж: 1

Айқындалмаған түрде берілген функциясының (0;-1) нүктесіндегі туындысын тап

Ж: 1/2

Айқындалмаған түрде берілген функциясының (8;1) нүктесіндегі туындысын тап

Ж: 2

,мұнда , екінші ретті дифференциалдық теңдеуі не деп атайды? Ж: Біртекті, сызықты тұрақты коэффициент

, мұнда ,- екінші ретті дифференциалдық теңдеуі не деп аталады? Ж: Біртекті емес, сызықты тұрақты коэффициент

- біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық теңдеуін қандай түрде береді

Ж: ak²+bk+c=0

, - біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық теңдеуінің түбірлерінің қосындысын табыңыз

Ж: -b/a

, - біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық теңдеуінің - түбірлерінің көбейтіндісі неге тең?

Ж: с/а

Ауыспа таңбалы қатарының жинақты болу шартын көрсетіңіз

Ж: а₁> a₂>…>a_n>… lim a_n=0

дәрежелік қатардың жинақтылық радиусын көрсетіңіз

Ж: R=1/lim

$$$ 316

қатарының абсолют жинақты болу шартын көрсетіңіз Ж: a₁ + a₂ + a₃ +…+ a_n + … жинақты

қатарының шартты жинақты болуының анықтамасы

Ж: а_n қатар жинақсыз, ал

а_n қатар жинақты

Ақиқат оқиғаның ықтималдығы тең:

Ж: 1

Атқыштың нысанаға тигізу ықтималдығы 0,7-ге тең. Оның нысанаға атқан екі оғының екеуінің де нысанаға тию ықтималдығын тап

Ж: 0,49

Әрбір 10 лоторея билетінің 2-еуі ұтысты. Кездейсоқ сатып алынған 5 билеттің 2-еуі ұтысты билет болу ықтималдығын тап

Ж: С²₅ (0,2)² (0,8)³

Бб- Гг

Біртекті пластинканың массасы былай табылады:

Ж: dxdy

Бернулли формуласын көрсет (мұндағы - оқиғасының бір тәжірибеде орындалу, ал сол тәжірибеде орындалмау ықтималдықтары)

Ж: P_n(k)= C^k_n p^k q^n-k

Бас дисперсия тең (мұндағы - бас орта)

Ж: D_r=1/N N_r(x₁-x_r)²

Гармоникалық қатарды көрсетіңіз

Ж: 1/n

Дд

Дәрежелік қатардың жинақтылық радиусын көрсетіңіз

Ж: R=lim |a_n / a_n+1|

Дисперсия мына формуламен есептелінеді

Ж: D= x ² – [x]²

Дисперсияны есептеу формуласын табыңыз

Ж: D = x² - [x]²

Дискретті кездейсоқ шаманың математикалық үмітін көрсетіңіз

Ж: =x₁p₁ + x₂p₂ + … + x_n p_n

Ее

Егер нүктесі функцияның нүктесіндегі шегі болса, онда

Ж: lim f(x,y)

Есепте Ж: 8

Екі айнымалы функциясының нүктесінде экстремум болуының қажетті шартын көрсет:

Ж: z^/_x=0 z^/_y=0

Екі айнымалы функцияның толық өсімше ұғымына қай формула сәйкес келеді

Ж: f (x+ x, y+ y) -f (x,y)

Екі айнымалы функцияның - бойынша алынған дербес өсімше ұғымына қай формула сәйкес келеді

Ж: f(x+ x, y) –f (x, y)

Екі айнымалы функцияның - бойынша алынған дербес өсімше ұғымына қай формула сәйкес келеді

Ж:f (x, y+ y) –f (x,y)

Егер дифференциалдық теңдеуі үшін шарты орындалса, онда бұл теңдеуді не деп атайды?

Ж: толық дифференцалды теңдеу

Егер , біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеудің сипаттамалық түбірлері нақты болып және болса, онда жалпы шешім қандай түрде беріледі:

Ж:y=c₁e^{k x} +c₂ e^{k x}

Егер , біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеуінің сипаттамалық түбірлері нақты және болса, онда жалпы шешім қандай түрде жазылады?

Ж: y=(c₁+c₂x)*e^kx

Егер - біртекті, сызықты, тұрақты коэффициентті дифференциалдық теңдеуінің сипаттамалық түбірлері комплекс сандар болса, онда жалпы шешім қандай түрде жазылады?

Ж: y=e ^x(c₁cos x + c₂ sin x)

Егер аралығында және тәуелсіз функциялар болса, онда - Вронский анықтауышы кез-келген х-үшін қандай шартты қанағаттандырады:

Ж: W=0

Егер аралығында және тәуелді функциялар болса, онда -Вронский анықтауышы кез-келген х-үшін қандай шартты қанағаттандырады?

Ж: W=0

Егер интегралында алмастыруын жасасақ, онда көшу Якобианы неге тең?

Ж: p

Егер , мұндағы және аймақтарының шекаралары ортақ, онда

Ж: f (x, y)dxdy+ f (x,y)dxdy

Егер болса, онда

Ж: C f (x, y) dxdy

Егер функциясы аймағында үзіліссіз болса, онда екі еселі интеграл нені білдіреді? Ж: табаны D болатын цилиндрдің көлемін

Егероблысы, ,мұндағы , қисықтарымен шектелген және функциялары кесіндісінде үзіліссіз болса, онда

Ж: dx f (x, y)dy

Егераймағы , ,мұндағы қисықтарымен шектелген және функциялары кесіндісінде үзіліссіз болса, онда

Ж: dy f (x, y) dx

Егер , онда

Ж: dx dy f (x, y, z) dz

Егер интегралдау аймағы тік бұрышты параллелипипед болса, онда

Ж: dx dy f (x, y, z) dz

функциясының Маклорен қатарына жіктелуін көрсетіңіз

Ж: e^x=1+x+x²/x!+x³/3!+…+xⁿ/n!+...

Егер сандық қатар жинақты болса, онда

Ж: lim a_n=0

Егер және қатарларының мүшелері үшін теңсіздіктер орындалса, онда

Ж: b_n қатарының жинақтылығынан а_n қатардың жинақтылығы шығады

Егер болса, онда дәрежелік қатарының жинақтылық радиусы неге тең?

Ж: R=lim a_n/ a_n+1

Егер дәрежелік қатары нөлге тең емес нүктесінде жинақты болса, онда

Ж: |x| < |x₀| тендігін қанағат-н барлық х-тер үшін абсолют жинақты

Егер дәрежелік - қатары нүктесінде жинақсыз болса, онда ол

Ж: |х| > |х₀| тендігін қанағат-н барлық х-тер үшін жинақсыз болады

Егер қатары жинақты болса, онда қатары туралы не айтуға болады?

Ж: жинақты

Егер қатары нүктесінде жинақты болса, онда қатарЖ: |х| < |x₀| болғанда әрбір х нүктесінде жинақты

Екі үйлесімсіз А және В оқиғаларының қосындысының ықтималдығы тең:

Ж: P(AB)=P(A)+P(B)

Екі тәуелсіз оқиғалардың көбейтіндісінің ықтималдығы тең:

Ж: P(AB)=P(A)*P(B)

Екі тәуелді оқиғалардың көбейтіндісінің ықтималдығы тең:

Ж: P(AB)=P(A)*P_A(B)

Екі үйлесімді оқиғалардың қосындысының ықтималдығы тең:

Ж:P (A+B)=P(A)+P(B)-P(AB)

Екі аңшы түлкіге бір уақытта оқ атады. Әр аңшының түлкіге тигізу ықтималды 1/3-ге тең. Түлкінің атылған болу ықтималдығы неге тең?

Ж: 4/9

Екі атқыш бір-біріне тәуелсіз бір нысанаға оқ атқан. Бірінші атқыштың нысанаға тигізу ықтималдығы 0,7-ге, ал екіншісінікі – 0,6-ға тең. Нысанаға оқтың тиген болу ықтималдығын тап

Ж:0,88

Екі монетаны қатарынан лақтырғанда екеуінде де «герб» түсу ықтималдығы неге тең?

Ж: 1/4

Жж

Жазықтықтағы және нүктелерінің арақашықтығын тап

Ж: 2 2

Жазықтықтағы және нүктелерінің арақашықтығын тап

Ж: 5

Жазықтықтағы және нүктелерінің арақашықтығын тап

Ж: 5

Жазықтықтағы және нүктелерінің арақашықтығын тап

Ж:5

Жәшіктегі бірдей 50 деталдың 5-і боялған. Кез келген детал алынды. Алынған деталдың боялған болу ықтималдығын табыңыз

Ж:0,1

Жәшікте 4 ақ және 8 қызыл шарлар бар. Жәшіктен кездейсоқ алынған шардың қызыл шар болу ықтималдығын тап

Ж: 2/3

Жәшікте 5 ақ, 4 жасыл және 3 қызыл шарлар бар. Жәшіктен кездейсоқ алынған шардың боялған шар болу ықтималдығын тап

Ж:7/12

Жәшікте 50 бірдей деталдар бар, оның ішінде 5 боялған кездейсоқ бір деталь алынсын. Осы алынған деталдың боялған детал болу ықтималдығы неге тең?

Ж: 0,1

М

және нүктелерінің арақашықтығы жазықтығында формуласы арқылы анықталады:

Ж: R=+ (x₂-x₁)²+(y₂-y₁)²

нүктелерінің тізбегінің шегі, нүктесі болады, егер Ж:0

- нүктесі кем дегенде екі рет дифференциалданатын функциясының максимум нүктесі болу үшін қандай шарт орындалады

Ж: =AC-B²>0, A<0

- нүктесі кем дегенде екі рет дифференциалданатын функциясының минимум нүктесі болу үшін қандай шарт орындалады

Ж: =AC-B²>0, A>0

Мына , () сандық қатары үшін дұрыс тұжырымды көрсетіңіз

Ж: a>1 қатар жинақты

Мүмкін емес оқиғаның ықтималдығы тең:

Ж: 0

Монетаны (тиынды) екі рет лақтырғанда кемінде бір рет «герб» түсу ықтималдығын тап

Ж: 3/4

Ии

Интегралды есептеңіз:

Ж: 9

Интегралды есептеңіз: Ж:4

Интегралды есептеңіз:

Ж:32

Интегралды есептеңіз:

Ж:2/ 3

Интегралды есептеңіз:

Ж: П/ 8

Интегралды есептеңіз:

Ж: П/ 2

Интегралды есептеңіз:

Ж: 4/3

Интегралды есептеңіз:

Ж: 8

Интегралды есептеңіз:

Ж: 9

Интегралды есептеңіз:

Ж: 8/ 3

Интегралды есептеңіз:

Ж:7

Интегралды есептеңіз:

Ж:8

Интегралды есептеңіз:

Ж:2

Интегралды есептеңіз:

Ж:2

Интегралды есептеңіз:

Ж: 1

Интегралды есептеңіз:

Ж: 2

Интегралды есептеңіз:

Ж: 2П/ 3

Интегралды есептеңіз:

Ж: 26

Интегралды есептеңіз:

Ж: 4

Интегралды есептеңіз: Ж: 36

Интегралды есептеңіз:

Ж:9/ 2

Интегралды есептеңіз: Ж: 4

Интегралды есептеңіз: Ж: 16/3

Интегралды есептеңіз: Ж: 16/ 3

Интегралды есептеңіз:

Ж: 18

Интегралды есептеңіз: Ж: 3

Интегралды есептеңіз: Ж: 3/ 4

Интегралды есептеңіз: Ж: 6

Интегралды есептеңіз: Ж:16

Интегралды есептеңіз: Ж:2

Интегралды есептеңіз:

Ж: П²/ 4

Интегралды есептеңіз:

Ж: 4

Интегралды есептеңіз:

Ж: П²/ 3

Интегралды есептеңіз: Ж:3

Интегралды есептеңіз: Ж:6

Интегралды есептеңіз:

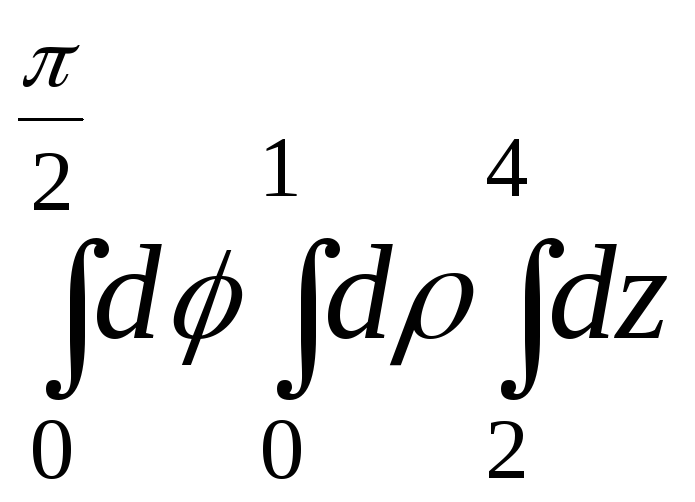
Ж:П

Интегралды есептеңіз: Ж:9

Интегралды есептеңіз:

Ж:П

Интегралдық функция арқылы берілген Х кездейсоқ шаманың математикалық үмітін тап

Ж: M (X) =1 / 8

Кк

Кеңістікте нүктесі арқылы бетіне жүргізілген жанама жазықтықтың теңдеуін тап:

Ж: 4x+y-2z-3=0

Кеңістікте нүктесі арқылы бетіне жүргізілген жанама жазықтықтың теңдеуін тап:

Ж: 3x-2y+3z=0

Кеңістікте нүктесі арқылы бетіне жүргізілген нормаль теңдеуді тап:

Ж:x-1/4=y-1/1=z-1/-2

Кеңістікте нүктесі арқылы бетіне жүргізілген нормаль теңдеуді тап:

Ж: x-1/4=y-2/1=z-5/-2

Кем дегенде екі рет дифференцилданатын функциясының нүктесінде экстремум болмауының шартын көрсет

Ж: =AC-B²<0

Оо

Оқиғаның ықтималдығы тең болуы мүмкін:

Ж: [ 0, 1]

Ойын сүйегін бір рет лақтырғанда оның жоғарғы жағына тақ сандардың түсу ықтималдығын тап Ж: 1/ 2

Ойын сүйегін лақтырғанда оның жоғарғы жағына түскен санның 3-ке еселі болу ықтималдығын тап Ж: 1/ 3

Тт

Төменде көрсетілген формулалардың ішінде қайсысы екі айнымалы функцияның градиентін көрсетеді

Ж: grad f( f/ x, f/ y)

Теңдеуді шешіңіз:

Ж: y=1/3sin3x+C

Теңдеуді шешіңіз:

Ж: y=-2e^-5x+C

Теңдеуді шешіңіз:

Ж: y=C(x+2)

Теңдеуді шешіңіз:

Ж: y=C*sinx

Теңдеуді шешіңіз:

Ж: y=C(x²+1)

Теңдеуді шешіңіз:

Ж: y-y²=x³+x+C

Теңдеуді шешіңіз:

Ж: 3y²+5y=sinx+C

Теңдеуді шешіңіз:

Ж: y=C*e^2x

Теңдеуді шешіңіз:

Ж: y=C*e^-5x

Теңдеуді шешіңіз:

Ж: y=c/x

Теңдеуді шешіңіз:

Ж: y=c/ cosx

Теңдеуді шешіңіз:

Ж: y=e^3x+C*e^2x

Теңдеуді шешіңіз:

Ж: y=e^-2x+C e^-3x

Теңдеуді шешіңіз:

Ж: x²+y²=C

Теңдеуді шешіңіз:

Ж: y²-x²=C

Теңдеуді шешіңіз:

Ж: y=x⁵+C x²

Теңдеуді шешіңіз: